Translated From: e-maxx.ru

Suffix Automaton (Suffix Automaton)

Suffix automaton là một cấu trúc dữ liệu mạnh mẽ cho phép giải quyết nhiều vấn đề liên quan đến chuỗi.

Ví dụ: bạn có thể tìm kiếm tất cả các lần xuất hiện của một chuỗi trong chuỗi khác hoặc đếm số lượng các chuỗi con khác nhau của một chuỗi đã cho. Cả hai nhiệm vụ đều có thể được giải quyết trong thời gian tuyến tính với sự trợ giúp của suffix automaton.

Về mặt trực quan, suffix automaton có thể được hiểu là một dạng nén của tất cả các chuỗi con của một chuỗi nhất định. Một thực tế ấn tượng là suffix automaton chứa tất cả thông tin này ở dạng nén cao. Đối với chuỗi có độ dài $n$, nó chỉ yêu cầu bộ nhớ $O(n)$. Hơn nữa, nó cũng có thể được xây dựng trong thời gian $O(n)$ (nếu chúng ta coi kích thước $k$ của bảng chữ cái là hằng số), nếu không thì cả độ phức tạp thời gian và bộ nhớ sẽ là $O(n \log k)$.

Tính tuyến tính của kích thước suffix automaton được phát hiện lần đầu tiên vào năm 1983 bởi Blumer và cộng sự, và vào năm 1985, các thuật toán tuyến tính đầu tiên để xây dựng đã được trình bày bởi Crochemore và Blumer.

Định nghĩa suffix automaton (Definition of a suffix automaton)

Suffix automaton cho một chuỗi $s$ nhất định là một DFA (deterministic finite automaton - automaton đơn định hữu hạn) tối thiểu chấp nhận tất cả các hậu tố của chuỗi $s$.

Nói cách khác:

• Suffix automaton là một đồ thị có hướng không có chu trình. Các đỉnh được gọi là trạng thái (states) và các cạnh được gọi là chuyển đổi (transitions) giữa các trạng thái.
• Một trong những trạng thái $t_0$ là trạng thái ban đầu, và nó phải là nguồn của đồ thị (tất cả các trạng thái khác đều có thể truy cập được từ $t_0$).
• Mỗi chuyển đổi được gắn nhãn với một số ký tự. Tất cả các chuyển đổi bắt nguồn từ một trạng thái phải có nhãn khác nhau.
• Một hoặc nhiều trạng thái được đánh dấu là trạng thái kết thúc (terminal states). Nếu chúng ta bắt đầu từ trạng thái ban đầu $t_0$ và di chuyển dọc theo các chuyển đổi đến trạng thái kết thúc, thì các nhãn của các chuyển đổi đã qua phải đánh vần một trong các hậu tố của chuỗi $s$. Mỗi hậu tố của $s$ phải có thể đánh vần được bằng cách sử dụng một đường dẫn từ $t_0$ đến một trạng thái kết thúc.
• Suffix automaton chứa số lượng đỉnh tối thiểu trong số tất cả các automaton thỏa mãn các điều kiện được mô tả ở trên.

Thuộc tính chuỗi con (Substring property)

Thuộc tính đơn giản và quan trọng nhất của suffix automaton là nó chứa thông tin về tất cả các chuỗi con của chuỗi $s$. Bất kỳ đường dẫn nào bắt đầu ở trạng thái ban đầu $t_0$, nếu chúng ta viết ra các nhãn của các chuyển đổi, sẽ tạo thành một chuỗi con của $s$. Và ngược lại, mọi chuỗi con của $s$ tương ứng với một đường dẫn nhất định bắt đầu tại $t_0$.

Để đơn giản hóa các giải thích, chúng tôi sẽ nói rằng chuỗi con tương ứng với đường dẫn đó (bắt đầu tại $t_0$ và các nhãn đánh vần chuỗi con). Và ngược lại, chúng tôi nói rằng bất kỳ đường dẫn nào cũng tương ứng với chuỗi được đánh vần bởi các nhãn của nó.

Một hoặc nhiều đường dẫn có thể dẫn đến một trạng thái. Do đó, chúng tôi sẽ nói rằng một trạng thái tương ứng với tập hợp các chuỗi, tương ứng với các đường dẫn này.

Ví dụ về suffix automata đã xây dựng (Examples of constructed suffix automata)

Ở đây chúng tôi sẽ hiển thị một số ví dụ về suffix automata cho một số chuỗi đơn giản.

Chúng tôi sẽ biểu thị trạng thái ban đầu bằng màu xanh lam và các trạng thái kết thúc bằng màu xanh lục.

Đối với chuỗi $s =~ \text{""}$:

Đối với chuỗi $s =~ \text{"a"}$:

Đối với chuỗi $s =~ \text{"aa"}$:

Đối với chuỗi $s =~ \text{"ab"}$:

Đối với chuỗi $s =~ \text{"aba"}$:

Đối với chuỗi $s =~ \text{"abb"}$:

Đối với chuỗi $s =~ \text{"abbb"}$:

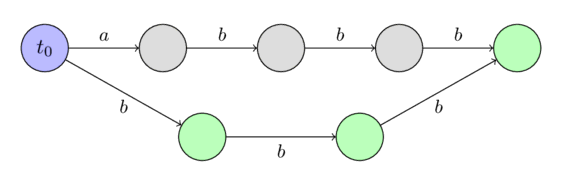
Xây dựng trong thời gian tuyến tính (Construction in linear time)

Trước khi mô tả thuật toán để xây dựng một suffix automaton trong thời gian tuyến tính, chúng ta cần giới thiệu một vài khái niệm mới và các bằng chứng đơn giản, sẽ rất quan trọng trong việc tìm hiểu việc xây dựng.

Vị trí kết thúc $endpos$ (End positions $endpos$)

Xét bất kỳ chuỗi con không rỗng $t$ nào của chuỗi $s$. Chúng tôi sẽ ký hiệu với $endpos(t)$ tập hợp tất cả các vị trí trong chuỗi $s$, trong đó các lần xuất hiện của $t$ kết thúc. Ví dụ: chúng ta có $endpos(\text{"bc"}) = \{2, 4\}$ cho chuỗi $\text{"abcbc"}$.

Chúng tôi sẽ gọi hai chuỗi con $t_1$ và $t_2$ là $endpos$-tương đương, nếu tập hợp kết thúc của chúng trùng nhau: $endpos(t_1) = endpos(t_2)$. Do đó, tất cả các chuỗi con không rỗng của chuỗi $s$ có thể được phân tách thành một số lớp tương đương theo tập hợp $endpos$ của chúng.

Hóa ra, trong một máy hậu tố, các chuỗi con $endpos$-tương đương tương ứng với cùng một trạng thái. Nói cách khác, số lượng trạng thái trong suffix automaton bằng số lượng các lớp tương đương trong tất cả các chuỗi con, cộng với trạng thái ban đầu. Mỗi trạng thái của một suffix automaton tương ứng với một hoặc nhiều chuỗi con có cùng giá trị $endpos$.

Sau này chúng tôi sẽ mô tả thuật toán xây dựng sử dụng giả định này. Sau đó chúng ta sẽ thấy, tất cả các thuộc tính cần thiết của một suffix automaton, ngoại trừ tính tối thiểu, đều được đáp ứng. Và tính tối thiểu tuân theo định lý Nerode (sẽ không được chứng minh trong bài viết này).

Chúng ta có thể đưa ra một số quan sát quan trọng liên quan đến các giá trị $endpos$:

Bổ đề 1: Hai chuỗi con không rỗng $u$ và $w$ (với $length(u) \le length(w)$) là $endpos$-tương đương, khi và chỉ khi chuỗi $u$ xuất hiện trong $s$ chỉ dưới dạng hậu tố của $w$.

Bằng chứng là hiển nhiên. Nếu $u$ và $w$ có cùng giá trị $endpos$, thì $u$ là hậu tố của $w$ và chỉ xuất hiện dưới dạng hậu tố của $w$ trong $s$. Và nếu $u$ là hậu tố của $w$ và chỉ xuất hiện dưới dạng hậu tố trong $s$, thì các giá trị $endpos$ bằng nhau theo định nghĩa.

Bổ đề 2: Xét hai chuỗi con không rỗng $u$ và $w$ (với $length(u) \le length(w)$). Khi đó tập hợp $endpos$ của chúng hoặc hoàn toàn không giao nhau, hoặc $endpos(w)$ là một tập hợp con của $endpos(u)$. Và nó phụ thuộc vào việc $u$ có phải là hậu tố của $w$ hay không.

$$\begin{cases} endpos(w) \subseteq endpos(u) & \text{nếu } u \text{ là hậu tố của } w \\\\ endpos(w) \cap endpos(u) = \emptyset & \text{ngược lại} \end{cases}$$

Bằng chứng: Nếu các tập hợp $endpos(u)$ và $endpos(w)$ có ít nhất một phần tử chung, thì các chuỗi $u$ và $w$ đều kết thúc ở vị trí đó, tức là $u$ là một hậu tố của $w$. Nhưng sau đó tại mỗi lần xuất hiện của $w$ cũng xuất hiện chuỗi con $u$, có nghĩa là $endpos(w)$ là một tập hợp con của $endpos(u)$.

Bổ đề 3: Xét một lớp tương đương $endpos$. Sắp xếp tất cả các chuỗi con trong lớp này theo độ dài giảm dần. Khi đó trong chuỗi kết quả, mỗi chuỗi con sẽ ngắn hơn chuỗi trước đó một đơn vị, và đồng thời sẽ là hậu tố của chuỗi trước đó. Nói cách khác, trong cùng một lớp tương đương, các chuỗi con ngắn hơn thực sự là các hậu tố của các chuỗi con dài hơn và chúng nhận tất cả các độ dài có thể trong một khoảng nhất định $[x; y]$.

Bằng chứng: Cố định một số lớp tương đương $endpos$. Nếu nó chỉ chứa một chuỗi, thì bổ đề rõ ràng là đúng. Bây giờ giả sử số lượng chuỗi trong lớp lớn hơn một.

Theo Bổ đề 1, hai chuỗi tương đương $endpos$ khác nhau luôn theo cách sao cho chuỗi ngắn hơn là hậu tố thực sự của chuỗi dài hơn. Do đó, không thể có hai chuỗi có cùng độ dài trong lớp tương đương.

Hãy ký hiệu $w$ là chuỗi dài nhất và $u$ là chuỗi ngắn nhất trong lớp tương đương. Theo Bổ đề 1, chuỗi $u$ là hậu tố thực sự của chuỗi $w$. Bây giờ hãy xem xét bất kỳ hậu tố nào của $w$ có độ dài trong khoảng $[length(u); length(w)]$. Dễ thấy rằng hậu tố này cũng được chứa trong cùng một lớp tương đương. Bởi vì hậu tố này chỉ có thể xuất hiện dưới dạng hậu tố của $w$ trong chuỗi $s$ (vì hậu tố ngắn hơn $u$ cũng xuất hiện trong $s$ chỉ dưới dạng hậu tố của $w$). Do đó, theo Bổ đề 1, hậu tố này $endpos$-tương đương với chuỗi $w$.

Liên kết hậu tố $link$ (Suffix links $link$)

Xem xét một số trạng thái $v \ne t_0$ trong automaton. Như chúng ta đã biết, trạng thái $v$ tương ứng với lớp chuỗi có cùng giá trị $endpos$. Và nếu chúng ta ký hiệu $w$ là chuỗi dài nhất trong các chuỗi này, thì tất cả các chuỗi khác là hậu tố của $w$.

Chúng tôi cũng biết một vài hậu tố đầu tiên của một chuỗi $w$ (nếu chúng ta xem xét các hậu tố theo thứ tự độ dài giảm dần) đều được chứa trong lớp tương đương này, và tất cả các hậu tố khác (ít nhất một hậu tố khác - hậu tố rỗng) nằm trong một số lớp khác. Chúng tôi ký hiệu $t$ là hậu tố lớn nhất như vậy và tạo một liên kết hậu tố đến nó.

Nói cách khác, một liên kết hậu tố (suffix link) $link(v)$ dẫn đến trạng thái tương ứng với hậu tố dài nhất của $w$ nằm trong một lớp tương đương $endpos$ khác.

Ở đây chúng tôi giả định rằng trạng thái ban đầu $t_0$ tương ứng với lớp tương đương của riêng nó (chỉ chứa chuỗi rỗng) và để thuận tiện, chúng tôi đặt $endpos(t_0) = \{-1, 0, \dots, length(s)-1\}$.

Bổ đề 4: Các liên kết hậu tố tạo thành một cây với gốc $t_0$.

Bằng chứng: Xét một trạng thái $v \ne t_0$ tùy ý. Một liên kết hậu tố $link(v)$ dẫn đến một trạng thái tương ứng với các chuỗi có độ dài nhỏ hơn nghiêm ngặt (điều này tuân theo định nghĩa của các liên kết hậu tố và từ Bổ đề 3). Do đó, bằng cách di chuyển dọc theo các liên kết hậu tố, sớm hay muộn chúng ta cũng sẽ đến trạng thái ban đầu $t_0$, tương ứng với chuỗi rỗng.

Bổ đề 5: Nếu chúng ta xây dựng một cây sử dụng các tập hợp $endpos$ (theo quy tắc tập hợp của nút cha chứa các tập hợp của tất cả con cái dưới dạng tập hợp con), thì cấu trúc sẽ trùng với cây của các liên kết hậu tố.

Bằng chứng: Việc chúng ta có thể xây dựng một cây bằng cách sử dụng các tập hợp $endpos$ tuân theo trực tiếp từ Bổ đề 2 (rằng bất kỳ hai tập hợp nào không giao nhau hoặc một tập hợp được chứa trong tập hợp kia).

Bây giờ chúng ta hãy xem xét một trạng thái $v \ne t_0$ tùy ý và liên kết hậu tố của nó $link(v)$. Từ định nghĩa của liên kết hậu tố và từ Bổ đề 2 suy ra rằng

$$endpos(v) \subseteq endpos(link(v)),$$

cùng với bổ đề trước chứng minh khẳng định: cây liên kết hậu tố về cơ bản là một cây của các tập hợp $endpos$.

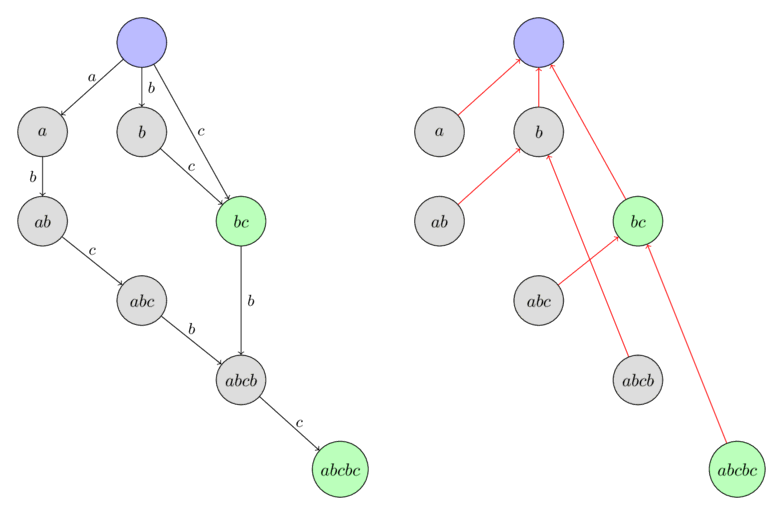
Dưới đây là một ví dụ về cây liên kết hậu tố trong suffix automaton được xây dựng cho chuỗi $\text{"abcbc"}$. Các nút được gắn nhãn với chuỗi con dài nhất từ lớp tương đương tương ứng.

Tóm tắt (Recap)

Trước khi tiến hành thuật toán, chúng ta tóm tắt lại kiến thức đã tích lũy và giới thiệu một vài ký hiệu phụ trợ.

• Các chuỗi con của chuỗi $s$ có thể được phân tách thành các lớp tương đương theo vị trí kết thúc $endpos$ của chúng.
• Suffix automaton bao gồm trạng thái ban đầu $t_0$, cũng như một trạng thái cho mỗi lớp tương đương $endpos$.
• Đối với mỗi trạng thái $v$, một hoặc nhiều chuỗi con khớp với nhau. Chúng tôi ký hiệu $longest(v)$ là chuỗi dài nhất như vậy và qua $len(v)$ là độ dài của nó. Chúng tôi ký hiệu $shortest(v)$ là chuỗi con ngắn nhất như vậy và độ dài của nó với $minlen(v)$. Sau đó, tất cả các chuỗi tương ứng với trạng thái này là các hậu tố khác nhau của chuỗi $longest(v)$ và có tất cả các độ dài có thể trong khoảng $[minlen(v); len(v)]$.
• Đối với mỗi trạng thái $v \ne t_0$, một liên kết hậu tố được định nghĩa là một liên kết, dẫn đến một trạng thái tương ứng với hậu tố của chuỗi $longest(v)$ có độ dài $minlen(v) - 1$. Các liên kết hậu tố tạo thành một cây với gốc ở $t_0$, và đồng thời cây này tạo thành mối quan hệ bao gồm giữa các tập hợp $endpos$.
• Chúng ta có thể biểu thị $minlen(v)$ cho $v \ne t_0$ bằng liên kết hậu tố $link(v)$ như sau:

$$minlen(v) = len(link(v)) + 1$$

• Nếu chúng ta bắt đầu từ một trạng thái $v_0$ tùy ý và đi theo các liên kết hậu tố, thì sớm hay muộn chúng ta cũng sẽ đạt đến trạng thái ban đầu $t_0$. Trong trường hợp này, chúng ta thu được một chuỗi các khoảng rời rạc $[minlen(v_i); len(v_i)]$, trong đó hợp lại tạo thành khoảng liên tục $[0; len(v_0)]$.

Thuật toán (Algorithm)

Bây giờ chúng ta có thể tiến hành thuật toán chính nó. Thuật toán sẽ là trực tuyến, tức là chúng ta sẽ thêm các ký tự của chuỗi từng cái một, và sửa đổi automaton cho phù hợp trong từng bước.

Để đạt được mức tiêu thụ bộ nhớ tuyến tính, chúng ta sẽ chỉ lưu trữ các giá trị $len$, $link$ và danh sách các chuyển đổi trong mỗi trạng thái. Chúng tôi sẽ không gắn nhãn các trạng thái kết thúc (nhưng sau này chúng tôi sẽ chỉ ra cách sắp xếp các nhãn này sau khi xây dựng suffix automaton).

Ban đầu automaton bao gồm một trạng thái duy nhất $t_0$, sẽ là chỉ số $0$ (các trạng thái còn lại sẽ nhận được các chỉ số $1, 2, \dots$). Chúng tôi gán cho nó $len = 0$ và $link = -1$ để thuận tiện ($-1$ sẽ là một trạng thái hư cấu, không tồn tại).

Bây giờ toàn bộ nhiệm vụ rút gọn lại thành việc thực hiện quá trình thêm một ký tự $c$ vào cuối chuỗi hiện tại. Hãy mô tả quá trình này:

• Gọi $last$ là trạng thái tương ứng với toàn bộ chuỗi trước khi thêm ký tự $c$. (Ban đầu chúng ta đặt $last = 0$, và chúng ta sẽ thay đổi $last$ trong bước cuối cùng của thuật toán cho phù hợp.)
• Tạo một trạng thái mới $cur$, và gán cho nó $len(cur) = len(last) + 1$. Giá trị $link(cur)$ không được biết vào lúc đó.
• Bây giờ chúng ta thực hiện thủ tục sau: Chúng ta bắt đầu ở trạng thái $last$. Trong khi không có chuyển đổi qua chữ cái $c$, chúng ta sẽ thêm một chuyển đổi đến trạng thái $cur$, và đi theo liên kết hậu tố. Nếu tại một thời điểm nào đó đã tồn tại một chuyển đổi qua chữ cái $c$, thì chúng ta sẽ dừng lại và biểu thị trạng thái này bằng $p$.
• Nếu chúng ta chưa tìm thấy trạng thái $p$ như vậy, thì chúng ta đã đạt đến trạng thái hư cấu $-1$, sau đó chúng ta chỉ cần gán $link(cur) = 0$ và rời đi.
• Giả sử bây giờ chúng ta đã tìm thấy một trạng thái $p$, từ đó tồn tại một chuyển đổi qua chữ cái $c$. Chúng tôi sẽ biểu thị trạng thái mà chuyển đổi dẫn đến là $q$.
• Bây giờ chúng ta có hai trường hợp. Hoặc $len(p) + 1 = len(q)$, hoặc không.
• Nếu $len(p) + 1 = len(q)$, thì chúng ta chỉ cần gán $link(cur) = q$ và rời đi.

• Nếu không thì phức tạp hơn một chút. Cần phải nhân bản (clone) trạng thái $q$: chúng ta tạo một trạng thái mới $clone$, sao chép tất cả dữ liệu từ $q$ (liên kết hậu tố và chuyển đổi) ngoại trừ giá trị $len$. Chúng tôi sẽ gán $len(clone) = len(p) + 1$.

  Sau khi nhân bản, chúng ta hướng liên kết hậu tố từ $cur$ đến $clone$, và cả từ $q$ đến $clone$.

  Cuối cùng, chúng ta cần đi bộ từ trạng thái $p$ trở lại bằng cách sử dụng các liên kết hậu tố miễn là có chuyển đổi qua $c$ đến trạng thái $q$, và chuyển hướng tất cả những chuyển đổi đó đến trạng thái $clone$.

• Trong bất kỳ trường hợp nào trong ba trường hợp, sau khi hoàn thành thủ tục, chúng ta cập nhật giá trị $last$ với trạng thái $cur$.

Nếu chúng ta cũng muốn biết trạng thái nào là kết thúc và trạng thái nào không, chúng ta có thể tìm thấy tất cả các trạng thái kết thúc sau khi xây dựng suffix automaton hoàn chỉnh cho toàn bộ chuỗi $s$. Để làm điều này, chúng ta lấy trạng thái tương ứng với toàn bộ chuỗi (được lưu trữ trong biến $last$) và đi theo các liên kết hậu tố của nó cho đến khi chúng ta đến trạng thái ban đầu. Chúng tôi sẽ đánh dấu tất cả các trạng thái đã truy cập là kết thúc. Dễ hiểu rằng bằng cách làm như vậy, chúng ta sẽ đánh dấu chính xác các trạng thái tương ứng với tất cả các hậu tố của chuỗi $s$, đó chính xác là các trạng thái kết thúc.

Trong phần tiếp theo, chúng ta sẽ xem xét chi tiết từng bước và cho thấy tính chính xác của nó.

Ở đây chúng tôi chỉ lưu ý rằng, vì chúng tôi chỉ tạo một hoặc hai trạng thái mới cho mỗi ký tự của $s$, suffix automaton chứa một số lượng trạng thái tuyến tính.

Tính tuyến tính của số lượng chuyển đổi, và nói chung là tính tuyến tính của thời gian chạy của thuật toán ít rõ ràng hơn, và chúng sẽ được chứng minh sau khi chúng tôi chứng minh tính chính xác.

Tính chính xác (Correctness)

• Chúng tôi sẽ gọi một chuyển đổi $(p, q)$ là liên tục (continuous) nếu $len(p) + 1 = len(q)$. Việc khác, tức là khi $len(p) + 1 < len(q)$, chuyển đổi sẽ được gọi là không liên tục (non-continuous).

  Như chúng ta có thể thấy từ mô tả của thuật toán, các chuyển đổi liên tục và không liên tục sẽ dẫn đến các trường hợp khác nhau của thuật toán. Các chuyển đổi liên tục là cố định và sẽ không bao giờ thay đổi nữa. Ngược lại, chuyển đổi không liên tục có thể thay đổi khi các chữ cái mới được thêm vào chuỗi (kết thúc của cạnh chuyển đổi có thể thay đổi).

• Để tránh sự mơ hồ, chúng tôi sẽ biểu thị chuỗi, mà suffix automaton được xây dựng trước khi thêm ký tự hiện tại $c$, bằng $s$.

• Thuật toán bắt đầu bằng cách tạo một trạng thái mới $cur$, sẽ tương ứng với toàn bộ chuỗi $s + c$. Rõ ràng là tại sao chúng ta phải tạo ra một trạng thái mới. Cùng với ký tự mới, một lớp tương đương mới được tạo ra.

• Sau khi tạo trạng thái mới, chúng ta duyệt qua các liên kết hậu tố bắt đầu từ trạng thái tương ứng với toàn bộ chuỗi $s$. Đối với mỗi trạng thái, chúng tôi cố gắng thêm một chuyển đổi với ký tự $c$ vào trạng thái mới $cur$. Do đó, chúng ta thêm ký tự $c$ vào mỗi hậu tố của $s$. Tuy nhiên, chúng ta chỉ có thể thêm các chuyển đổi mới này nếu chúng không xung đột với một chuyển đổi đã tồn tại. Do đó, ngay khi chúng ta tìm thấy một chuyển đổi đã tồn tại với $c$, chúng ta phải dừng lại.

• Trong trường hợp đơn giản nhất, chúng tôi đã đạt đến trạng thái hư cấu $-1$. Điều này có nghĩa là chúng ta đã thêm chuyển đổi với $c$ cho tất cả các hậu tố của $s$. Điều này cũng có nghĩa là, ký tự $c$ chưa từng là một phần của chuỗi $s$ trước đây. Do đó, liên kết hậu tố của $cur$ phải dẫn đến trạng thái $0$.

• Trong trường hợp thứ hai, chúng ta bắt gặp một chuyển đổi hiện có $(p, q)$. Điều này có nghĩa là chúng ta đã cố gắng thêm một chuỗi $x + c$ (trong đó $x$ là hậu tố của $s$) vào máy đã tồn tại trong máy (chuỗi $x + c$ đã xuất hiện dưới dạng chuỗi con của $s$). Vì chúng tôi giả định rằng automaton cho chuỗi $s$ được xây dựng chính xác, chúng tôi không nên thêm một chuyển đổi mới ở đây.

  Tuy nhiên có một khó khăn. Liên kết hậu tố từ trạng thái $cur$ nên dẫn đến trạng thái nào? Chúng ta phải tạo một liên kết hậu tố đến một trạng thái, trong đó chuỗi dài nhất chính xác là $x + c$, tức là $len$ của trạng thái này phải là $len(p) + 1$. Tuy nhiên, có thể trạng thái như vậy chưa tồn tại, tức là $len(q) > len(p) + 1$. Trong trường hợp này, chúng ta phải tạo ra một trạng thái như vậy bằng cách tách trạng thái $q$.

• Nếu chuyển đổi $(p, q)$ hóa ra là liên tục, thì $len(q) = len(p) + 1$. Trong trường hợp này mọi thứ đều đơn giản. Chúng tôi hướng liên kết hậu tố từ $cur$ đến trạng thái $q$.

• Nếu không, quá trình chuyển đổi là không liên tục, tức là $len(q) > len(p) + 1$. Điều này có nghĩa là trạng thái $q$ tương ứng không chỉ với hậu tố của $s + c$ với độ dài $len(p) + 1$, mà còn với các chuỗi con dài hơn của $s$. Chúng ta không thể làm gì khác ngoài tách trạng thái $q$ thành hai trạng thái con, để trạng thái đầu tiên có độ dài $len(p) + 1$.

  Làm thế nào chúng ta có thể tách một trạng thái? Chúng ta nhân bản trạng thái $q$, cung cấp cho chúng ta trạng thái $clone$, và chúng ta đặt $len(clone) = len(p) + 1$. Chúng tôi sao chép tất cả các chuyển đổi từ $q$ sang $clone$, vì chúng tôi không muốn thay đổi các đường dẫn đi qua $q$. Ngoài ra, chúng tôi đặt liên kết hậu tố từ $clone$ thành đích của liên kết hậu tố của $q$, và đặt liên kết hậu tố của $q$ thành $clone$.

  Và sau khi tách trạng thái, chúng ta đặt liên kết hậu tố từ $cur$ đến $clone$.

  Trong bước cuối cùng, chúng tôi thay đổi một số chuyển đổi thành $q$, chúng tôi chuyển hướng chúng sang $clone$. Chúng ta phải thay đổi những chuyển đổi nào? Chỉ cần chuyển hướng các chuyển đổi tương ứng với tất cả các hậu tố của chuỗi $w + c$ (trong đó $w$ là chuỗi dài nhất của $p$) là đủ, tức là chúng ta cần tiếp tục di chuyển dọc theo các liên kết hậu tố, bắt đầu từ đỉnh $p$ cho đến khi chúng ta đến trạng thái hư cấu $-1$ hoặc một chuyển đổi dẫn đến trạng thái khác với $q$.

Số lượng hoạt động tuyến tính (Linear number of operations)

Đầu tiên, chúng ta ngay lập tức đưa ra giả định rằng kích thước của bảng chữ cái là hằng số. Nếu không phải như vậy, thì sẽ không thể nói về độ phức tạp thời gian tuyến tính. Danh sách các chuyển đổi từ một đỉnh sẽ được lưu trữ trong một cây cân bằng, cho phép bạn nhanh chóng thực hiện các thao tác tìm kiếm khóa và thêm khóa. Do đó, nếu chúng ta biểu thị kích thước của bảng chữ cái bằng $k$, thì hành vi tiệm cận của thuật toán sẽ là $O(n \log k)$ với bộ nhớ $O(n)$. Tuy nhiên, nếu bảng chữ cái đủ nhỏ, thì bạn có thể hy sinh bộ nhớ bằng cách tránh các cây cân bằng và lưu trữ các chuyển đổi tại mỗi đỉnh dưới dạng một mảng có độ dài $k$ (để tìm kiếm nhanh bằng khóa) và danh sách động (để nhanh chóng duyệt qua tất cả các khóa có sẵn). Do đó, chúng ta đạt được độ phức tạp thời gian $O(n)$ cho thuật toán, nhưng với chi phí là độ phức tạp bộ nhớ $O(n k)$.

Vì vậy, chúng tôi sẽ coi kích thước của bảng chữ cái là hằng số, tức là mỗi thao tác tìm kiếm chuyển đổi trên một ký tự, thêm chuyển đổi, tìm kiếm chuyển đổi tiếp theo - tất cả các thao tác này đều có thể được thực hiện trong $O(1)$.

Nếu chúng ta xem xét tất cả các phần của thuật toán, thì nó chứa ba vị trí trong thuật toán mà độ phức tạp tuyến tính không rõ ràng:

• Vị trí đầu tiên là truyền qua các liên kết hậu tố từ trạng thái $last$, thêm các chuyển đổi với ký tự $c$.
• Vị trí thứ hai là sao chép các chuyển đổi khi trạng thái $q$ được nhân bản thành một trạng thái mới $clone$.
• Vị trí thứ ba là thay đổi quá trình chuyển đổi dẫn đến $q$, chuyển hướng chúng đến $clone$.

Chúng tôi sử dụng thực tế là kích thước của suffix automaton (cả về số lượng trạng thái và số lượng chuyển đổi) là tuyến tính. (Bằng chứng về tính tuyến tính của số lượng trạng thái là chính thuật toán, và bằng chứng về tính tuyến tính của số lượng trạng thái được đưa ra bên dưới, sau khi thực hiện thuật toán).

Do đó, tổng độ phức tạp của vị trí thứ nhất và thứ hai là hiển nhiên, sau cùng thì mỗi thao tác chỉ thêm một chuyển đổi mới được khấu hao vào automaton.

Vẫn còn phải ước tính tổng độ phức tạp của vị trí thứ ba, trong đó chúng ta chuyển hướng các chuyển đổi, ban đầu trỏ đến $q$, sang $clone$. Chúng tôi ký hiệu $v = longest(p)$. Đây là hậu tố của chuỗi $s$, và với mỗi lần lặp, độ dài của nó giảm dần - và do đó vị trí $v$ là hậu tố của chuỗi $s$ tăng đơn điệu với mỗi lần lặp. Trong trường hợp này, nếu trước lần lặp đầu tiên của vòng lặp, chuỗi tương ứng $v$ ở độ sâu $k$ ($k \ge 2$) từ $last$ (bằng cách đếm độ sâu là số lượng liên kết hậu tố), thì sau lần lặp cuối cùng chuỗi $v + c$ sẽ là liên kết hậu tố thứ $2$ trên đường dẫn từ $cur$ (sẽ trở thành giá trị $last$ mới).

Do đó, mỗi lần lặp của vòng lặp này dẫn đến thực tế là vị trí của chuỗi $longest(link(link(last))$ là hậu tố của chuỗi hiện tại sẽ tăng đơn điệu. Do đó, chu trình này không thể được thực hiện quá $n$ lần lặp, đó là điều cần thiết để chứng minh.

Cài đặt (Implementation)

Đầu tiên, chúng tôi mô tả một cấu trúc dữ liệu sẽ lưu trữ tất cả thông tin về một chuyển đổi cụ thể ($len$, $link$ và danh sách chuyển đổi). Nếu cần, bạn có thể thêm cờ đầu cuối tại đây, cũng như thông tin khác. Chúng tôi sẽ lưu trữ danh sách các chuyển đổi dưới dạng $map$, cho phép chúng tôi đạt được tổng bộ nhớ $O(n)$ và $O(n \log k)$ thời gian để xử lý toàn bộ chuỗi.

suffix_automaton_struct

struct state {
    int len, link;
    map<char, int> next;
};

Bản thân suffix automaton sẽ được lưu trữ trong một mảng các cấu trúc này $state$. Chúng tôi lưu trữ kích thước hiện tại $sz$ và biến $last$, trạng thái tương ứng với toàn bộ chuỗi tại thời điểm này.

suffix_automaton_def

const int MAXLEN = 100000;
state st[MAXLEN * 2];
int sz, last;

Chúng tôi đưa ra một chức năng khởi tạo suffix automaton (tạo suffix automaton với một trạng thái duy nhất).

suffix_automaton_init

void sa_init() {
    st[0].len = 0;
    st[0].link = -1;
    sz++;
    last = 0;
}

Và cuối cùng chúng tôi đưa ra việc thực hiện chức năng chính - thêm ký tự tiếp theo vào cuối dòng hiện tại, xây dựng lại máy cho phù hợp.

suffix_automaton_extend

void sa_extend(char c) {
    int cur = sz++;
    st[cur].len = st[last].len + 1;
    int p = last;
    while (p != -1 && !st[p].next.count(c)) {
        st[p].next[c] = cur;
        p = st[p].link;
    }
    if (p == -1) {
        st[cur].link = 0;
    } else {
        int q = st[p].next[c];
        if (st[p].len + 1 == st[q].len) {
            st[cur].link = q;
        } else {
            int clone = sz++;
            st[clone].len = st[p].len + 1;
            st[clone].next = st[q].next;
            st[clone].link = st[q].link;
            while (p != -1 && st[p].next[c] == q) {
                st[p].next[c] = clone;
                p = st[p].link;
            }
            st[q].link = st[cur].link = clone;
        }
    }
    last = cur;
}

Như đã đề cập ở trên, nếu bạn hy sinh bộ nhớ ($O(n k)$, trong đó $k$ là kích thước bảng chữ cái), thì bạn có thể đạt được thời gian xây dựng máy trong $O(n)$, ngay cả đối với bất kỳ kích thước bảng chữ cái nào $k$. Nhưng đối với điều này, bạn sẽ phải lưu trữ một mảng có kích thước $k$ trong mỗi trạng thái (để nhanh chóng chuyển sang quá trình chuyển đổi của chữ cái), và thêm danh sách tất cả các chuyển đổi (để nhanh chóng lặp lại các chuyển đổi đó).

Thuộc tính bổ sung (Additional properties)

Số lượng trạng thái (Number of states)

Số lượng trạng thái trong suffix automaton của chuỗi $s$ có độ dài $n$ không vượt quá $2n - 1$ (với $n \ge 2$).

Bằng chứng là chính thuật toán xây dựng, vì ban đầu automaton bao gồm một trạng thái, và trong lần lặp đầu tiên và thứ hai, chỉ có một trạng thái duy nhất sẽ được tạo ra, và trong $n-2$ bước còn lại, tối đa $2$ trạng thái sẽ được tạo ra mỗi bước.

Tuy nhiên, chúng tôi cũng có thể hiển thị ước tính này mà không cần biết thuật toán. Chúng ta hãy nhớ lại rằng số lượng trạng thái bằng số lượng các tập hợp khác nhau $endpos$. Ngoài ra, các tập hợp $endpos$ này tạo thành một cây (đỉnh cha chứa tất cả các tập hợp con trong tập hợp của mình). Xem xét cây này và biến đổi nó một chút: miễn là nó có một đỉnh bên trong chỉ có một con (có nghĩa là tập hợp của con bỏ lỡ ít nhất một vị trí từ tập hợp cha), chúng tôi tạo một con mới với tập hợp các vị trí bị thiếu. Cuối cùng, chúng ta có một cái cây trong đó mỗi đỉnh bên trong có bậc lớn hơn một, và số lượng lá không vượt quá $n$. Do đó, không có quá $2n - 1$ đỉnh trong một cây như vậy.

Giới hạn về số lượng trạng thái này thực sự có thể đạt được cho mỗi $n$. Một chuỗi có thể là:

$$\text{"abbb}\dots \text{bbb"}$$

Trong mỗi lần lặp, bắt đầu từ lần thứ ba, thuật toán sẽ tách một trạng thái, dẫn đến chính xác $2n - 1$ trạng thái.

Số lượt chuyển đổi (Number of transitions)

Số lần chuyển đổi trong một suffix automaton của một chuỗi $s$ có độ dài $n$ không vượt quá $3n - 4$ (với $n \ge 3$).

Hãy chứng minh điều này:

Trước tiên chúng ta hãy ước tính số lượng chuyển đổi liên tục. Xem xét một cây bao trùm các đường dẫn dài nhất trong automaton bắt đầu ở trạng thái $t_0$. Bộ xương này sẽ chỉ bao gồm các cạnh liên tục, và do đó số lượng của chúng nhỏ hơn số lượng trạng thái, tức là nó không vượt quá $2n - 2$.

Bây giờ chúng ta hãy ước tính số lượng chuyển đổi không liên tục. Gọi chuyển đổi không liên tục hiện tại là $(p, q)$ với ký tự $c$. Chúng tôi lấy chuỗi tương ứng $u + c + w$, trong đó chuỗi $u$ tương ứng với đường dẫn dài nhất từ trạng thái ban đầu đến $p$, và $w$ đến đường dẫn dài nhất từ $q$ đến bất kỳ trạng thái kết thúc nào. Một mặt, mỗi chuỗi như vậy $u + c + w$ cho mỗi chuỗi không hoàn chỉnh sẽ khác nhau (vì các chuỗi $u$ và $w$ chỉ được hình thành bởi các chuyển đổi hoàn chỉnh). Mặt khác, mỗi chuỗi như vậy $u + c + w$, theo định nghĩa của các trạng thái kết thúc, sẽ là hậu tố của toàn bộ chuỗi $s$. Vì chỉ có $n$ hậu tố không rỗng của $s$, và không có chuỗi nào trong số $u + c + w$ có thể chứa $s$ (bởi vì toàn bộ chuỗi chỉ chứa các chuyển đổi hoàn chỉnh), tổng số chuyển đổi không hoàn chỉnh không vượt quá $n - 1$.

Kết hợp hai ước tính này cho chúng ta giới hạn $3n - 3$. Tuy nhiên, vì số lượng trạng thái tối đa chỉ có thể đạt được với trường hợp thử nghiệm $\text{"abbb\dots bbb"}$ và trường hợp này rõ ràng có ít hơn $3n - 3$ chuyển đổi, chúng tôi nhận được giới hạn chặt chẽ hơn $3n - 4$ cho số lần chuyển đổi trong một suffix automaton.

Giới hạn này cũng có thể đạt được với chuỗi:

$$\text{"abbb}\dots \text{bbbc"}$$

Ứng dụng (Applications)

Ở đây chúng ta xem xét một số nhiệm vụ có thể được giải quyết bằng cách sử dụng suffix automaton. Để đơn giản, chúng tôi giả định rằng kích thước bảng chữ cái $k$ là không đổi, điều này cho phép chúng tôi xem xét độ phức tạp của việc gắn thêm một ký tự và truyền tải là hằng số.

Kiểm tra sự xuất hiện (Check for occurrence)

Cho một văn bản $T$, và nhiều mẫu $P$. Chúng ta phải kiểm tra xem các chuỗi $P$ có xuất hiện dưới dạng chuỗi con của $T$ hay không.

Chúng tôi xây dựng một suffix automaton của văn bản $T$ trong thời gian $O(length(T))$. Để kiểm tra xem mẫu $P$ có xuất hiện trong $T$ hay không, chúng tôi làm theo các chuyển đổi, bắt đầu từ $t_0$, theo các ký tự của $P$. Nếu tại một thời điểm nào đó không tồn tại một chuyển đổi, thì mẫu $P$ không xuất hiện dưới dạng chuỗi con của $T$. Nếu chúng ta có thể xử lý toàn bộ chuỗi $P$ theo cách này, thì chuỗi xuất hiện trong $T$.

Rõ ràng là điều này sẽ mất thời gian $O(length(P))$ cho mỗi chuỗi $P$. Hơn nữa, thuật toán thực sự tìm thấy độ dài của tiền tố dài nhất của $P$ xuất hiện trong văn bản.

Số lượng chuỗi con khác nhau (Number of different substrings)

Cho một chuỗi $S$. Bạn muốn tính toán số lượng chuỗi con khác nhau.

Chúng ta hãy xây dựng một suffix automaton cho chuỗi $S$.

Mỗi chuỗi con của $S$ tương ứng với một số đường dẫn trong automaton. Do đó số chuỗi con khác nhau bằng số đường dẫn khác nhau trong automaton bắt đầu từ $t_0$.

Cho rằng suffix automaton là một đồ thị có hướng không có chu trình, số lượng các cách khác nhau có thể được tính bằng cách sử dụng quy hoạch động.

Cụ thể, đặt $d[v]$ là số cách, bắt đầu ở trạng thái $v$ (bao gồm cả đường dẫn có độ dài bằng 0). Sau đó chúng ta có đệ quy:

$$d[v] = 1 + \sum_{w : (v, w, c) \in DAWG} d[w]$$

Tức là $d[v]$ có thể được biểu thị bằng tổng các câu trả lời cho tất cả các đầu của quá trình chuyển đổi của $v$.

Số lượng chuỗi con khác nhau là giá trị $d[t_0] - 1$ (vì chúng ta không tính chuỗi con rỗng).

Tổng độ phức tạp thời gian: $O(length(S))$

Ngoài ra, chúng ta có thể tận dụng lợi thế của thực tế là mỗi trạng thái $v$ khớp với các chuỗi con có độ dài $[minlen(v),len(v)]$. Do đó, với $minlen(v) = 1 + len(link(v))$, chúng ta có tổng số chuỗi con riêng biệt ở trạng thái $v$ là $len(v) - minlen(v) + 1 = len(v) - (1 + len(link(v))) + 1 = len(v) - len(link(v))$.

Điều này được chứng minh ngắn gọn dưới đây:

long long get_diff_strings(){
    long long tot = 0;
    for(int i = 1; i < sz; i++) {
        tot += st[i].len - st[st[i].link].len;
    }
    return tot;
}

Mặc dù đây cũng là $O(length(S))$, nhưng nó không yêu cầu thêm không gian và không có lệnh gọi đệ quy, do đó chạy nhanh hơn trong thực tế.

Tổng độ dài của tất cả các chuỗi con khác nhau (Total length of all different substrings)

Cho một chuỗi $S$. Chúng tôi muốn tính toán tổng độ dài của tất cả các chuỗi con khác nhau của nó.

Giải pháp tương tự như giải pháp trước, chỉ bây giờ cần phải xem xét hai đại lượng cho phần quy hoạch động: số lượng chuỗi con khác nhau $d[v]$ và tổng độ dài của chúng $ans[v]$.

Chúng tôi đã mô tả cách tính $d[v]$ trong tác vụ trước. Giá trị $ans[v]$ có thể được tính bằng đệ quy:

$$ans[v] = \sum_{w : (v, w, c) \in DAWG} d[w] + ans[w]$$

Chúng ta lấy câu trả lời của mỗi đỉnh liền kề $w$, và thêm vào đó $d[w]$ (vì mỗi chuỗi con dài hơn một ký tự khi bắt đầu từ trạng thái $v$).

Một lần nữa nhiệm vụ này có thể được tính toán trong thời gian $O(length(S))$.

Ngoài ra, một lần nữa, chúng ta có thể tận dụng lợi thế của thực tế là mỗi trạng thái $v$ khớp với các chuỗi con có độ dài $[minlen(v),len(v)]$. Vì $minlen(v) = 1 + len(link(v))$ và công thức chuỗi số học $S_n = n \cdot \frac{a_1+a_n}{2}$ (trong đó $S_n$ biểu thị tổng của $n$ số hạng, $a_1$ đại diện cho số hạng đầu tiên và $a_n$ đại diện cho số hạng cuối cùng), chúng ta có thể tính độ dài của chuỗi con ở trạng thái trong thời gian không đổi. Sau đó, chúng tôi tổng hợp các tổng này cho từng trạng thái $v \neq t_0$ trong automaton. Điều này được hiển thị bằng mã dưới đây:

long long get_tot_len_diff_substings() {
    long long tot = 0;
    for(int i = 1; i < sz; i++) {
        long long shortest = st[st[i].link].len + 1;
        long long longest = st[i].len;

        long long num_strings = longest - shortest + 1;
        long long cur = num_strings * (longest + shortest) / 2;
        tot += cur;
    }
    return tot;
}

Cách tiếp cận này chạy trong thời gian $O(length(S))$, nhưng thực nghiệm chạy nhanh hơn 20 lần so với phiên bản quy hoạch động đã ghi nhớ trên các chuỗi ngẫu nhiên. Nó không đòi hỏi thêm không gian và không cần đệ quy.

Chuỗi con thứ $k$ theo thứ tự từ điển (Lexicographically $k$-th substring)

Cho một chuỗi $S$. Chúng tôi phải trả lời nhiều câu hỏi. Đối với mỗi số đã cho $K_i$ chúng ta phải tìm chuỗi thứ $K_i$ trong danh sách sắp xếp theo thứ tự từ điển của tất cả các chuỗi con.

Giải pháp cho vấn đề này dựa trên ý tưởng của hai vấn đề trước đó. Chuỗi con thứ $k$ theo từ điển tương ứng với đường dẫn thứ $k$ theo từ điển trong suffix automaton. Do đó, sau khi đếm số lượng đường dẫn từ mỗi trạng thái, chúng ta có thể dễ dàng tìm kiếm đường dẫn thứ $k$ bắt đầu từ gốc của automaton.

Việc này mất thời gian $O(length(S))$ để tiền xử lý và sau đó $O(length(ans) \cdot k)$ cho mỗi truy vấn (trong đó $ans$ là câu trả lời cho truy vấn và $k$ là kích thước của bảng chữ cái).

Dịch chuyển vòng nhỏ nhất (Smallest cyclic shift)

Cho một chuỗi $S$. Chúng tôi muốn tìm sự thay đổi theo chu kỳ nhỏ nhất theo từ điển.

Chúng tôi xây dựng một suffix automaton cho chuỗi $S + S$. Sau đó, automaton sẽ chứa trong chính nó dưới dạng đường dẫn tất cả các dịch chuyển vòng của chuỗi $S$.

Do đó, vấn đề giảm xuống thành việc tìm đường dẫn nhỏ nhất theo từ điển có độ dài $length(S)$, có thể được thực hiện theo cách tầm thường: chúng ta bắt đầu ở trạng thái ban đầu và tham lam đi qua các chuyển đổi với ký tự tối thiểu.

Tổng độ phức tạp thời gian là $O(length(S))$.

Số lần xuất hiện (Number of occurrences)

Cho một văn bản $T$. Chúng tôi phải trả lời nhiều câu hỏi. Đối với mỗi mẫu đã cho $P$ chúng ta phải tìm hiểu xem chuỗi $P$ xuất hiện bao nhiêu lần trong chuỗi $T$ dưới dạng một chuỗi con.

Chúng tôi xây dựng suffix automaton cho văn bản $T$.

Tiếp theo chúng tôi thực hiện tiền xử lý sau: đối với mỗi trạng thái $v$ trong automaton, chúng ta tính số $cnt[v]$ bằng với kích thước của tập hợp $endpos(v)$. Trong thực tế, tất cả các chuỗi tương ứng với cùng một trạng thái $v$ đều xuất hiện trong văn bản $T$ một lượng lần bằng nhau, bằng với số lượng vị trí trong tập hợp $endpos$.

Tuy nhiên, chúng ta không thể xây dựng các tập hợp $endpos$ một cách rõ ràng, vì vậy chúng ta chỉ xem xét kích thước của chúng $cnt$.

Để tính toán chúng, chúng ta tiến hành như sau. Đối với mỗi trạng thái, nếu nó không được tạo bằng cách nhân bản (và nếu nó không phải là trạng thái ban đầu $t_0$), chúng tôi khởi tạo nó với $cnt = 1$. Sau đó, chúng tôi sẽ đi qua tất cả các trạng thái theo thứ tự độ dài $len$ giảm dần và thêm giá trị hiện tại $cnt[v]$ vào các liên kết hậu tố:

$$cnt[link(v)] \text{ += } cnt[v]$$

Điều này cung cấp giá trị chính xác cho từng trạng thái.

Tại sao điều này đúng? Tổng số trạng thái thu được không qua nhân bản chính xác là $length(T)$, và $i$ trạng thái đầu tiên trong số đó xuất hiện khi chúng ta thêm $i$ ký tự đầu tiên. Do đó, đối với mỗi trạng thái này, chúng tôi đếm vị trí tương ứng mà nó được xử lý. Do đó, ban đầu chúng ta có $cnt = 1$ cho mỗi trạng thái như vậy và $cnt = 0$ cho tất cả các trạng thái khác.

Sau đó, chúng tôi áp dụng thao tác sau cho mỗi $v$: $cnt[link(v)] \text{ += } cnt[v]$. Ý nghĩa đằng sau điều này là, nếu một chuỗi $v$ xuất hiện $cnt[v]$ lần, thì tất cả các hậu tố của nó cũng xuất hiện tại các vị trí kết thúc chính xác giống nhau, do đó cũng $cnt[v]$ lần.

Tại sao chúng ta không đếm quá nhiều trong thủ tục này (tức là không đếm một số vị trí hai lần)? Bởi vì chúng ta chỉ thêm các vị trí của một trạng thái vào một trạng thái khác, vì vậy không thể xảy ra trường hợp một trạng thái hướng các vị trí của nó sang trạng thái khác hai lần theo hai cách khác nhau.

Do đó, chúng ta có thể tính toán số lượng $cnt$ cho tất cả các trạng thái trong automaton trong thời gian $O(length(T))$.

Sau đó trả lời một truy vấn bằng cách chỉ tìm kiếm giá trị $cnt[t]$, trong đó $t$ là trạng thái tương ứng với mẫu, nếu trạng thái đó tồn tại. Nếu không thì trả lời bằng $0$. Trả lời một truy vấn mất thời gian $O(length(P))$.

Vị trí xuất hiện đầu tiên (First occurrence position)

Cho một văn bản $T$ và nhiều truy vấn. Đối với mỗi chuỗi truy vấn $P$, chúng tôi muốn tìm vị trí xuất hiện đầu tiên của $P$ trong chuỗi $T$ (vị trí bắt đầu của $P$).

Chúng ta lại xây dựng một suffix automaton. Ngoài ra, chúng tôi tính toán trước vị trí $firstpos$ cho tất cả các trạng thái trong automaton, tức là đối với mỗi trạng thái $v$, chúng ta muốn tìm vị trí $firstpos[v]$ của phần cuối của lần xuất hiện đầu tiên. Nói cách khác, chúng ta muốn tìm trước phần tử tối thiểu của mỗi tập hợp $endpos$ (vì rõ ràng không thể duy trì tất cả các tập hợp $endpos$ một cách rõ ràng).

Để duy trì các vị trí này $firstpos$, chúng tôi mở rộng chức năng sa_extend(). Khi chúng ta tạo một trạng thái mới $cur$, chúng ta đặt:

$$firstpos(cur) = len(cur) - 1$$

Và khi chúng ta sao chép một đỉnh $q$ dưới dạng $clone$, chúng ta đặt:

$$firstpos(clone) = firstpos(q)$$

(vì tùy chọn duy nhất khác cho một giá trị sẽ là $firstpos(cur)$ chắc chắn quá lớn)

Do đó câu trả lời cho truy vấn chỉ đơn giản là $firstpos(t) - length(P) + 1$, trong đó $t$ là trạng thái tương ứng với chuỗi $P$. Trả lời một truy vấn một lần nữa chỉ mất thời gian $O(length(P))$.

Tất cả vị trí xuất hiện (All occurrence positions)

Lần này chúng ta phải hiển thị tất cả các vị trí xuất hiện trong chuỗi $T$.

Một lần nữa chúng tôi xây dựng một suffix automaton cho văn bản $T$. Tương tự như trong nhiệm vụ trước, chúng ta tính toán vị trí $firstpos$ cho tất cả các trạng thái.

Rõ ràng $firstpos(t)$ là một phần của câu trả lời, nếu $t$ là trạng thái tương ứng với một chuỗi truy vấn $P$. Vì vậy, chúng tôi đã tính đến trạng thái của automaton chứa $P$. Chúng ta cần tính đến những trạng thái nào khác? Tất cả các trạng thái tương ứng với các chuỗi mà $P$ là hậu tố. Nói cách khác, chúng ta cần tìm tất cả các trạng thái có thể đến trạng thái $t$ thông qua các liên kết hậu tố.

Do đó để giải quyết vấn đề, chúng ta cần lưu danh sách các tham chiếu hậu tố dẫn đến từng trạng thái. Câu trả lời cho truy vấn sau đó sẽ chứa tất cả $firstpos$ cho mỗi trạng thái mà chúng ta có thể tìm thấy trên DFS / BFS bắt đầu từ trạng thái $t$ chỉ sử dụng các tham chiếu hậu tố.

Nhìn chung, điều này đòi hỏi $O(length (T))$ để tiền xử lý và $O(length(P) + answer(P))$ cho mỗi yêu cầu, ở đâu $answer(P)$ — đây là kích thước của câu trả lời.

Đầu tiên, chúng ta đi xuống automaton cho từng ký tự trong mẫu để tìm nút bắt đầu của chúng ta yêu cầu $O(length(P))$. Sau đó, chúng tôi sử dụng giải pháp thay thế của mình sẽ hoạt động kịp thời $O(answer(P))$, bởi vì chúng ta sẽ không ghé thăm một trạng thái hai lần (bởi vì chỉ có một liên kết hậu tố rời khỏi mỗi trạng thái, vì vậy không thể có hai con đường khác nhau dẫn đến cùng một trạng thái).

Chúng ta chỉ phải tính đến việc hai trạng thái khác nhau có thể có cùng giá trị $firstpos$. Điều này xảy ra nếu một trạng thái thu được bằng cách nhân bản trạng thái khác. Tuy nhiên, điều này không phá hỏng sự phức tạp, vì mỗi trạng thái chỉ có thể có tối đa một bản sao.

Hơn nữa, chúng ta cũng có thể loại bỏ các vị trí trùng lặp, nếu chúng ta không xuất các vị trí từ các trạng thái được sao chép. Trong thực tế, một trạng thái mà một trạng thái nhân bản có thể đạt được, cũng có thể truy cập được từ trạng thái ban đầu. Do đó, nếu chúng ta nhớ cờ is_cloned cho mỗi trạng thái, chúng ta chỉ cần bỏ qua các trạng thái được nhân bản và chỉ xuất $firstpos$ cho tất cả các trạng thái khác.

Dưới đây là một số bản phác thảo thực hiện:

struct state {
    ...
    bool is_clone;
    int first_pos;
    vector<int> inv_link;
};

// after constructing the automaton
for (int v = 1; v < sz; v++) {
    st[st[v].link].inv_link.push_back(v);
}

// output all positions of occurrences
void output_all_occurrences(int v, int P_length) {
    if (!st[v].is_clone)
        cout << st[v].first_pos - P_length + 1 << endl;
    for (int u : st[v].inv_link)
        output_all_occurrences(u, P_length);
}

Chuỗi không xuất hiện ngắn nhất (Shortest non-appearing string)

Cho một chuỗi $S$ và một bảng chữ cái nhất định. Chúng ta phải tìm một chuỗi có độ dài nhỏ nhất, không xuất hiện trong $S$.

Chúng tôi sẽ áp dụng quy hoạch động trên suffix automaton được xây dựng cho chuỗi $S$.

Gọi $d[v]$ là câu trả lời cho nút $v$, tức là chúng ta đã xử lý một phần của chuỗi con, hiện đang ở trạng thái $v$, và muốn tìm số lượng ký tự nhỏ nhất phải thêm vào để tìm một chuyển đổi không tồn tại. Tính toán $d[v]$ rất đơn giản. Nếu không có sự chuyển tiếp bằng cách sử dụng ít nhất một ký tự của bảng chữ cái, thì $d[v] = 1$. Nếu không, một ký tự là không đủ, và vì vậy chúng ta cần lấy tối thiểu tất cả các câu trả lời của tất cả các chuyển đổi:

$$d[v] = 1 + \min_{w:(v,w,c) \in SA} d[w].$$

Câu trả lời cho vấn đề sẽ là $d[t_0]$, và chuỗi thực tế có thể được khôi phục bằng cách sử dụng mảng được tính toán $d[]$.

Chuỗi con chung dài nhất của hai chuỗi (Longest common substring of two strings)

Cho hai chuỗi $S$ và $T$. Chúng ta phải tìm chuỗi con chung dài nhất, tức là một chuỗi $X$ xuất hiện dưới dạng chuỗi con trong $S$ và cả trong $T$.

Chúng tôi xây dựng một suffix automaton cho chuỗi $S$.

Bây giờ chúng ta sẽ lấy chuỗi $T$, và đối với mỗi tiền tố, hãy tìm hậu tố dài nhất của tiền tố này trong $S$. Nói cách khác, đối với mỗi vị trí trong chuỗi $T$, chúng tôi muốn tìm chuỗi con chung dài nhất của $S$ và $T$ kết thúc ở vị trí đó.

Đối với điều này, chúng tôi sẽ sử dụng hai biến, trạng thái hiện tại $v$, và độ dài hiện tại $l$. Hai biến này sẽ mô tả phần khớp hiện tại: độ dài của nó và trạng thái tương ứng với nó.

Ban đầu $v = t_0$ và $l = 0$, tức là trận đấu trống rỗng.

Bây giờ chúng ta hãy mô tả cách chúng ta có thể thêm một ký tự $T[i]$ và tính toán lại câu trả lời cho nó.

• Nếu có chuyển đổi từ $v$ với ký tự $T[i]$, thì chúng ta chỉ cần làm theo chuyển đổi và tăng $l$ thêm một.
• Nếu không có chuyển đổi như vậy, chúng ta phải rút ngắn phần khớp hiện tại, điều đó có nghĩa là chúng ta cần tuân theo liên kết hậu tố: $v = link(v)$. Đồng thời, độ dài hiện tại phải được rút ngắn. Rõ ràng chúng ta cần gán $l = len(v)$, vì sau khi đi qua liên kết hậu tố, chúng ta sẽ ở trạng thái có chuỗi dài nhất tương ứng là một chuỗi con.
• Nếu vẫn không có chuyển đổi bằng cách sử dụng ký tự bắt buộc, chúng tôi lặp lại và đi qua liên kết hậu tố và giảm $l$, cho đến khi chúng tôi tìm thấy một chuyển đổi hoặc chúng tôi đạt đến trạng thái hư cấu $-1$ (có nghĩa là biểu tượng $T[i]$ hoàn toàn không xuất hiện trong $S$, vì vậy chúng ta gán $v = l = 0$).

Câu trả lời cho nhiệm vụ sẽ là tối đa của tất cả các giá trị $l$.

Độ phức tạp của phần này là $O(length(T))$, vì trong một lần di chuyển, chúng ta có thể tăng $l$ lên một hoặc thực hiện một vài lần đi qua các liên kết hậu tố, mỗi lần đi qua sẽ giảm giá trị $l$.

Cài đặt:

string lcs (string S, string T) {
    sa_init();
    for (int i = 0; i < S.size(); i++)
        sa_extend(S[i]);

    int v = 0, l = 0, best = 0, bestpos = 0;
    for (int i = 0; i < T.size(); i++) {
        while (v && !st[v].next.count(T[i])) {
            v = st[v].link ;
            l = st[v].len;
        }
        if (st[v].next.count(T[i])) {
            v = st [v].next[T[i]];
            l++;
        }
        if (l > best) {
            best = l;
            bestpos = i;
        }
    }
    return T.substr(bestpos - best + 1, best);
} 

Chuỗi con chung lớn nhất của nhiều chuỗi (Largest common substring of multiple strings)

Có $k$ chuỗi $S_i$ được đưa ra. Chúng ta phải tìm chuỗi con chung dài nhất, tức là một chuỗi $X$ xuất hiện dưới dạng chuỗi con trong mỗi chuỗi $S_i$.

Chúng tôi nối tất cả các chuỗi thành một chuỗi lớn $T$, tách các chuỗi bằng một ký tự đặc biệt $D_i$ (mỗi chuỗi một ký tự):

$$T = S_1 + D_1 + S_2 + D_2 + \dots + S_k + D_k.$$

Sau đó, chúng tôi xây dựng suffix automaton cho chuỗi $T$.

Bây giờ chúng ta cần tìm một chuỗi trong máy, được chứa trong tất cả các chuỗi $S_i$, và điều này có thể được thực hiện bằng cách sử dụng các ký tự được thêm đặc biệt. Lưu ý rằng nếu một chuỗi con được bao gồm trong một số chuỗi $S_j$, thì trong suffix automaton tồn tại một đường dẫn bắt đầu từ chuỗi con này chứa ký tự $D_j$ và không chứa các ký tự khác $D_1, \dots, D_{j-1}, D_{j+1}, \dots, D_k$.

Do đó, chúng ta cần tính toán khả năng đạt được, cho chúng ta biết đối với từng trạng thái của máy và từng ký hiệu $D_i$ nếu tồn tại một đường dẫn như vậy. Điều này có thể dễ dàng được tính toán bởi DFS hoặc BFS và quy hoạch động. Sau đó, câu trả lời cho bài toán sẽ là chuỗi $longest(v)$ cho trạng thái $v$, từ đó các đường dẫn tồn tại cho tất cả các ký tự đặc biệt.

Bài tập (Practice Problems)

• CSES - Finding Patterns
• CSES - Counting Patterns
• CSES - String Matching
• CSES - Patterns Positions
• CSES - Distinct Substrings
• CSES - Word Combinations
• CSES - String Distribution
• AtCoder - K-th Substring
• SPOJ - SUBLEX
• Codeforces - Cyclical Quest
• Codeforces - String