Cây phân đoạn (Segment Tree)¶
Segment Tree (Cây phân đoạn) là một cấu trúc dữ liệu lưu trữ thông tin về các khoảng của mảng dưới dạng cây. Điều này cho phép trả lời các truy vấn đoạn trên một mảng một cách hiệu quả, trong khi vẫn đủ linh hoạt để cho phép sửa đổi nhanh mảng. Điều này bao gồm việc tìm tổng của các phần tử mảng liên tiếp $a[l \dots r]$, hoặc tìm phần tử nhỏ nhất trong một đoạn như vậy trong thời gian $O(\log n)$. Giữa việc trả lời các truy vấn như vậy, Segment Tree cho phép sửa đổi mảng bằng cách thay thế một phần tử, hoặc thậm chí thay đổi các phần tử của cả một đoạn con (ví dụ: gán tất cả các phần tử $a[l \dots r]$ cho bất kỳ giá trị nào, hoặc thêm một giá trị vào tất cả các phần tử trong đoạn con).
Nhìn chung, Segment Tree là một cấu trúc dữ liệu rất linh hoạt, và một số lượng lớn các bài toán có thể được giải quyết bằng nó. Ngoài ra, cũng có thể áp dụng các thao tác phức tạp hơn và trả lời các truy vấn phức tạp hơn (xem Các phiên bản nâng cao của Segment Trees). Đặc biệt, Segment Tree có thể dễ dàng được khái quát hóa cho các chiều lớn hơn. Ví dụ, với Segment Tree hai chiều, bạn có thể trả lời các truy vấn tổng hoặc giá trị nhỏ nhất trên một hình chữ nhật con của một ma trận đã cho chỉ trong thời gian $O(\log^2 n)$.
Một tính chất quan trọng của Segment Trees là chúng chỉ yêu cầu một lượng bộ nhớ tuyến tính. Segment Tree tiêu chuẩn cần $4n$ nút để làm việc trên một mảng có kích thước $n$.
Dạng đơn giản nhất của Segment Tree (Simplest form of a Segment Tree)¶
Để bắt đầu dễ dàng, chúng ta xem xét dạng đơn giản nhất của Segment Tree. Chúng ta muốn trả lời các truy vấn tổng một cách hiệu quả. Định nghĩa chính thức của nhiệm vụ của chúng ta là: Cho một mảng $a[0 \dots n-1]$, Segment Tree phải có khả năng tìm tổng của các phần tử giữa các chỉ số $l$ và $r$ (tức là tính tổng $\sum_{i=l}^r a[i]$), và cũng xử lý việc thay đổi giá trị của các phần tử trong mảng (tức là thực hiện các phép gán có dạng $a[i] = x$). Segment Tree phải có khả năng xử lý cả hai truy vấn trong thời gian $O(\log n)$.
Đây là một sự cải tiến so với các cách tiếp cận đơn giản hơn. Một cách cài đặt mảng đơn giản - chỉ sử dụng một mảng đơn giản - có thể cập nhật các phần tử trong $O(1)$, nhưng yêu cầu $O(n)$ để tính toán từng truy vấn tổng. Và tổng tiền tố được tính toán trước có thể tính toán các truy vấn tổng trong $O(1)$, nhưng việc cập nhật một phần tử mảng yêu cầu $O(n)$ thay đổi đối với tổng tiền tố.
Cấu trúc của Segment Tree (Structure of the Segment Tree)¶
Chúng ta có thể thực hiện cách tiếp cận chia để trị khi nói đến các đoạn mảng. Chúng ta tính toán và lưu trữ tổng của các phần tử của toàn bộ mảng, tức là tổng của đoạn $a[0 \dots n-1]$. Sau đó, chúng ta chia mảng thành hai nửa $a[0 \dots (n-1)/2]$ và $a[(n+1)/2 \dots n-1]$ và tính tổng của mỗi nửa và lưu trữ chúng. Mỗi nửa trong hai nửa này lần lượt được chia đôi, và cứ thế cho đến khi tất cả các đoạn đạt kích thước $1$.
Chúng ta có thể xem các đoạn này tạo thành một cây nhị phân: gốc của cây này là đoạn $a[0 \dots n-1]$, và mỗi nút (trừ các nút lá) có chính xác hai nút con. Đây là lý do tại sao cấu trúc dữ liệu được gọi là "Segment Tree", mặc dù trong hầu hết các triển khai, cây không được xây dựng một cách rõ ràng (xem Cài đặt).
Dưới đây là một biểu diễn trực quan của một Segment Tree như vậy trên mảng $a = [1, 3, -2, 8, -7]$:
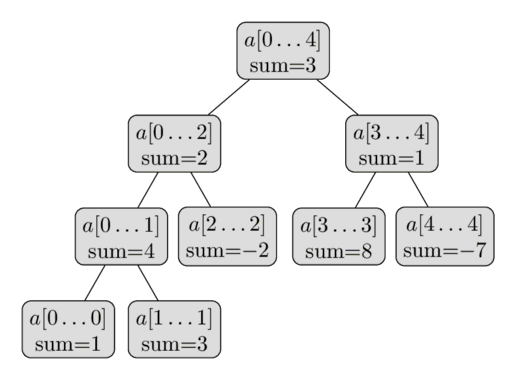
Từ mô tả ngắn gọn này về cấu trúc dữ liệu, chúng ta đã có thể kết luận rằng một Segment Tree chỉ yêu cầu một số lượng nút tuyến tính. Cấp đầu tiên của cây chứa một nút duy nhất (gốc), cấp thứ hai sẽ chứa hai nút, trong cấp thứ ba nó sẽ chứa bốn nút, cho đến khi số lượng nút đạt $n$. Do đó, số lượng nút trong trường hợp xấu nhất có thể được ước tính bằng tổng $1 + 2 + 4 + \dots + 2^{\lceil\log_2 n\rceil} \lt 2^{\lceil\log_2 n\rceil + 1} \lt 4n$.
Điều đáng chú ý là bất cứ khi nào $n$ không phải là lũy thừa của hai, không phải tất cả các cấp của Segment Tree sẽ được lấp đầy hoàn toàn. Chúng ta có thể thấy hành vi đó trong hình ảnh. Bây giờ chúng ta có thể quên đi thực tế này, nhưng nó sẽ trở nên quan trọng sau này trong quá trình cài đặt.
Chiều cao của Segment Tree là $O(\log n)$, bởi vì khi đi xuống từ gốc đến các lá, kích thước của các đoạn giảm khoảng một nửa.
Xây dựng (Construction)¶
Trước khi xây dựng segment tree, chúng ta cần quyết định:
- giá trị được lưu trữ tại mỗi nút của segment tree. Ví dụ, trong một segment tree tổng, một nút sẽ lưu trữ tổng của các phần tử trong phạm vi $[l, r]$ của nó.
- thao tác hợp nhất (merge) kết hợp hai anh em trong một segment tree. Ví dụ, trong một segment tree tổng, hai nút tương ứng với các phạm vi $a[l_1 \dots r_1]$ và $a[l_2 \dots r_2]$ sẽ được hợp nhất thành một nút tương ứng với phạm vi $a[l_1 \dots r_2]$ bằng cách cộng các giá trị của hai nút.
Lưu ý rằng một nút là một "nút lá", nếu đoạn tương ứng của nó chỉ bao gồm một giá trị trong mảng ban đầu. Nó có mặt ở cấp thấp nhất của một segment tree. Giá trị của nó sẽ bằng phần tử (tương ứng) $a[i]$.
Bây giờ, để xây dựng segment tree, chúng ta bắt đầu ở cấp dưới cùng (các nút lá) và gán cho chúng các giá trị tương ứng. Trên cơ sở các giá trị này, chúng ta có thể tính toán các giá trị của cấp trước đó, bằng cách sử dụng hàm merge.
Và trên cơ sở đó, chúng ta có thể tính toán các giá trị của cấp trước nữa, và lặp lại quy trình cho đến khi chúng ta đến nút gốc.
Thuận tiện để mô tả thao tác này một cách đệ quy theo hướng khác, tức là, từ nút gốc đến các nút lá. Thủ tục xây dựng, nếu được gọi trên một nút không phải lá, thực hiện như sau:
- xây dựng đệ quy các giá trị của hai nút con
- hợp nhất các giá trị đã tính toán của các con này.
Chúng ta bắt đầu xây dựng tại nút gốc, và do đó, chúng ta có thể tính toán toàn bộ segment tree.
Độ phức tạp thời gian của việc xây dựng này là $O(n)$, giả sử rằng thao tác hợp nhất là thời gian hằng số (thao tác hợp nhất được gọi $n$ lần, bằng số lượng các nút bên trong segment tree).
Truy vấn tổng (Sum queries)¶
Bây giờ chúng ta sẽ trả lời các truy vấn tổng. Là đầu vào, chúng ta nhận được hai số nguyên $l$ và $r$, và chúng ta phải tính tổng của đoạn $a[l \dots r]$ trong thời gian $O(\log n)$.
Để làm điều này, chúng ta sẽ duyệt qua Segment Tree và sử dụng các tổng đã tính toán trước của các đoạn. Giả sử rằng chúng ta hiện đang ở nút bao gồm đoạn $a[tl \dots tr]$. Có ba trường hợp có thể xảy ra.
Trường hợp dễ nhất là khi đoạn $a[l \dots r]$ bằng với đoạn tương ứng của nút hiện tại (tức là $a[l \dots r] = a[tl \dots tr]$), thì chúng ta đã hoàn thành và có thể trả về tổng đã tính toán trước được lưu trữ trong nút.
Ngoài ra, đoạn của truy vấn có thể rơi hoàn toàn vào miền của con trái hoặc con phải. Hãy nhớ lại rằng con trái bao gồm đoạn $a[tl \dots tm]$ và nút phải bao gồm đoạn $a[tm + 1 \dots tr]$ với $tm = (tl + tr) / 2$. Trong trường hợp này, chúng ta chỉ cần đi đến nút con, mà đoạn tương ứng bao gồm đoạn truy vấn, và thực thi thuật toán được mô tả ở đây với nút đó.
Và sau đó là trường hợp cuối cùng, đoạn truy vấn giao với cả hai con. Trong trường hợp này, chúng ta không có lựa chọn nào khác ngoài việc thực hiện hai cuộc gọi đệ quy, một cho mỗi con. Đầu tiên chúng ta đi đến con trái, tính toán câu trả lời một phần cho nút này (tức là tổng các giá trị của phần giao nhau giữa đoạn của truy vấn và đoạn của con trái), sau đó đi đến con phải, tính toán câu trả lời một phần bằng nút đó, và sau đó kết hợp các câu trả lời bằng cách cộng chúng lại. Nói cách khác, vì con trái đại diện cho đoạn $a[tl \dots tm]$ và con phải đại diện cho đoạn $a[tm+1 \dots tr]$, chúng ta tính toán truy vấn tổng $a[l \dots tm]$ bằng cách sử dụng con trái, và truy vấn tổng $a[tm+1 \dots r]$ bằng cách sử dụng con phải.
Vì vậy, xử lý truy vấn tổng là một hàm đệ quy tự gọi chính nó một lần với con trái hoặc con phải (không thay đổi ranh giới truy vấn), hoặc hai lần, một lần cho con trái và một lần cho con phải (bằng cách chia truy vấn thành hai truy vấn con). Và đệ quy kết thúc, bất cứ khi nào ranh giới của đoạn truy vấn hiện tại trùng với ranh giới của đoạn của nút hiện tại. Trong trường hợp đó, câu trả lời sẽ là giá trị đã tính toán trước của tổng của đoạn này, được lưu trữ trong cây.
Nói cách khác, việc tính toán truy vấn là một quá trình duyệt cây, lan truyền qua tất cả các nhánh cần thiết của cây, và sử dụng các giá trị tổng đã tính toán trước của các đoạn trong cây.
Rõ ràng chúng ta sẽ bắt đầu duyệt từ nút gốc của Segment Tree.
Thủ tục được minh họa trong hình ảnh sau. Một lần nữa mảng $a = [1, 3, -2, 8, -7]$ được sử dụng, và ở đây chúng ta muốn tính tổng $\sum_{i=2}^4 a[i]$. Các nút có màu sẽ được truy cập, và chúng ta sẽ sử dụng các giá trị đã tính toán trước của các nút màu xanh lá cây. Điều này cho chúng ta kết quả $-2 + 1 = -1$.
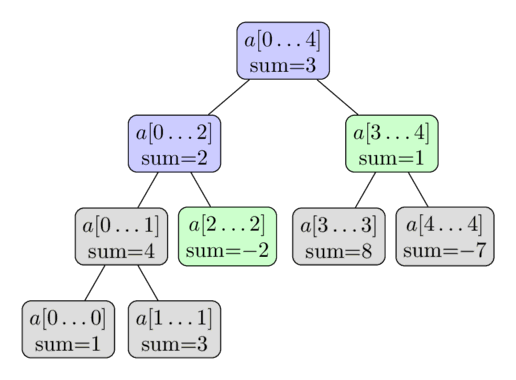
Tại sao độ phức tạp của thuật toán này là $O(\log n)$? Để hiển thị độ phức tạp này, chúng ta xem xét từng cấp của cây. Hóa ra, đối với mỗi cấp, chúng ta chỉ truy cập không quá bốn nút. Và vì chiều cao của cây là $O(\log n)$, chúng ta nhận được thời gian chạy mong muốn.
Chúng ta có thể chứng minh rằng mệnh đề này (tối đa bốn nút mỗi cấp) là đúng bằng quy nạp. Ở cấp độ đầu tiên, chúng ta chỉ truy cập một nút, nút gốc, vì vậy ở đây chúng ta truy cập ít hơn bốn nút. Bây giờ hãy nhìn vào một cấp độ tùy ý. Theo giả thuyết quy nạp, chúng ta truy cập tối đa bốn nút. Nếu chúng ta chỉ truy cập tối đa hai nút, cấp độ tiếp theo có tối đa bốn nút. Điều đó là tầm thường, bởi vì mỗi nút chỉ có thể gây ra tối đa hai cuộc gọi đệ quy. Vì vậy, hãy giả sử rằng chúng ta truy cập ba hoặc bốn nút trong cấp độ hiện tại. Từ những nút đó, chúng ta sẽ phân tích các nút ở giữa cẩn thận hơn. Vì truy vấn tổng yêu cầu tổng của một mảng con liên tục, chúng ta biết rằng các đoạn tương ứng với các nút được truy cập ở giữa sẽ được bao phủ hoàn toàn bởi đoạn của truy vấn tổng. Do đó, các nút này sẽ không thực hiện bất kỳ cuộc gọi đệ quy nào. Vì vậy, chỉ có nút ngoài cùng bên trái và nút ngoài cùng bên phải mới có tiềm năng thực hiện các cuộc gọi đệ quy. Và những nút đó sẽ chỉ tạo ra tối đa bốn cuộc gọi đệ quy, vì vậy cấp độ tiếp theo cũng sẽ thỏa mãn khẳng định. Chúng ta có thể nói rằng một nhánh tiếp cận ranh giới bên trái của truy vấn, và nhánh thứ hai tiếp cận ranh giới bên phải.
Do đó, chúng ta truy cập tối đa $4 \log n$ nút trong tổng số, và điều đó bằng với thời gian chạy là $O(\log n)$.
Tóm lại, truy vấn hoạt động bằng cách chia đoạn đầu vào thành nhiều đoạn con mà tất cả các tổng đã được tính toán trước và lưu trữ trong cây. Và nếu chúng ta ngừng phân chia bất cứ khi nào đoạn truy vấn trùng với đoạn nút, thì chúng ta chỉ cần $O(\log n)$ đoạn như vậy, điều này mang lại hiệu quả của Segment Tree.
Truy vấn cập nhật (Update queries)¶
Bây giờ chúng ta muốn sửa đổi một phần tử cụ thể trong mảng, giả sử chúng ta muốn thực hiện phép gán $a[i] = x$. Và chúng ta phải xây dựng lại Segment Tree, sao cho nó tương ứng với mảng mới, đã sửa đổi.
Truy vấn này dễ hơn truy vấn tổng. Mỗi cấp của một Segment Tree tạo thành một phân vùng của mảng. Do đó, một phần tử $a[i]$ chỉ đóng góp vào một đoạn từ mỗi cấp. Do đó chỉ có $O(\log n)$ nút cần được cập nhật.
Dễ thấy rằng, yêu cầu cập nhật có thể được thực hiện bằng cách sử dụng một hàm đệ quy. Hàm được chuyển qua nút cây hiện tại, và nó gọi đệ quy chính nó với một trong hai nút con (nút chứa $a[i]$ trong đoạn của nó), và sau đó tính toán lại giá trị tổng của nó, tương tự như cách nó được thực hiện trong phương thức build (đó là tổng của hai con của nó).
Một lần nữa đây là một hình ảnh trực quan sử dụng cùng một mảng. Ở đây chúng ta thực hiện cập nhật $a[2] = 3$. Các nút màu xanh lá cây là các nút mà chúng ta truy cập và cập nhật.
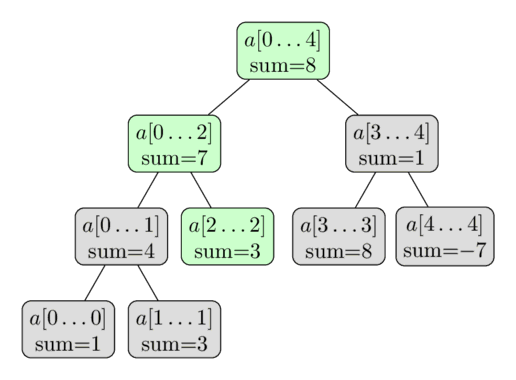
Cài đặt (Implementation)¶
Cân nhắc chính là cách lưu trữ Segment Tree. Tất nhiên chúng ta có thể định nghĩa một struct $\text{Vertex}$ và tạo các đối tượng, lưu trữ các ranh giới của đoạn, tổng của nó và thêm vào đó là các con trỏ đến các nút con của nó. Tuy nhiên, điều này đòi hỏi phải lưu trữ rất nhiều thông tin dư thừa dưới dạng các con trỏ. Chúng ta sẽ sử dụng một thủ thuật đơn giản để làm cho việc này hiệu quả hơn nhiều bằng cách sử dụng một cấu trúc dữ liệu ẩn (implicit data structure): Chỉ lưu trữ các tổng trong một mảng. (Một phương pháp tương tự được sử dụng cho binary heaps). Tổng của nút gốc tại chỉ số 1, tổng của hai nút con của nó tại các chỉ số 2 và 3, tổng của các con của hai nút đó tại các chỉ số 4 đến 7, v.v. Với chỉ số bắt đầu từ 1, thuận tiện là con trái của một nút tại chỉ số $i$ được lưu trữ tại chỉ số $2i$, và con phải tại chỉ số $2i + 1$. Tương đương, cha của một nút tại chỉ số $i$ được lưu trữ tại $i/2$ (phép chia số nguyên).
Điều này đơn giản hóa việc cài đặt rất nhiều. Chúng ta không cần lưu trữ cấu trúc của cây trong bộ nhớ. Nó được định nghĩa ngầm. Chúng ta chỉ cần một mảng chứa tổng của tất cả các đoạn.
Như đã lưu ý trước đây, chúng ta cần lưu trữ tối đa $4n$ nút. Nó có thể ít hơn, nhưng để thuận tiện chúng ta luôn cấp phát một mảng có kích thước $4n$. Sẽ có một số phần tử trong mảng tổng, sẽ không tương ứng với bất kỳ nút nào trong cây thực tế, nhưng điều này không làm phức tạp việc cài đặt.
Vì vậy, chúng ta lưu trữ Segment Tree đơn giản dưới dạng một mảng $t[]$ với kích thước gấp bốn lần kích thước đầu vào $n$:
int n, t[4*MAXN];
Thủ tục xây dựng Segment Tree từ một mảng $a[]$ đã cho trông như thế này: nó là một hàm đệ quy với các tham số $a[]$ (mảng đầu vào), $v$ (chỉ số của nút hiện tại), và các ranh giới $tl$ và $tr$ của đoạn hiện tại. Trong chương trình chính, hàm này sẽ được gọi với các tham số của nút gốc: $v = 1$, $tl = 0$, và $tr = n - 1$.
void build(int a[], int v, int tl, int tr) {
if (tl == tr) {
t[v] = a[tl];
} else {
int tm = (tl + tr) / 2;
build(a, v*2, tl, tm);
build(a, v*2+1, tm+1, tr);
t[v] = t[v*2] + t[v*2+1];
}
}
Hơn nữa, hàm để trả lời các truy vấn tổng cũng là một hàm đệ quy, nhận các tham số thông tin về nút/đoạn hiện tại (tức là chỉ số $v$ và các ranh giới $tl$ và $tr$) và cả thông tin về các ranh giới của truy vấn, $l$ và $r$. Để đơn giản hóa mã, hàm này luôn thực hiện hai cuộc gọi đệ quy, ngay cả khi chỉ cần một - trong trường hợp đó, cuộc gọi đệ quy thừa sẽ có $l > r$, và điều này có thể dễ dàng bị bắt bằng cách sử dụng một kiểm tra bổ sung ở đầu hàm.
int sum(int v, int tl, int tr, int l, int r) {
if (l > r)
return 0;
if (l == tl && r == tr) {
return t[v];
}
int tm = (tl + tr) / 2;
return sum(v*2, tl, tm, l, min(r, tm))
+ sum(v*2+1, tm+1, tr, max(l, tm+1), r);
}
Cuối cùng là truy vấn cập nhật. Hàm cũng sẽ nhận thông tin về nút/đoạn hiện tại, và thêm vào đó là tham số của truy vấn cập nhật (tức là vị trí của phần tử và giá trị mới của nó).
void update(int v, int tl, int tr, int pos, int new_val) {
if (tl == tr) {
t[v] = new_val;
} else {
int tm = (tl + tr) / 2;
if (pos <= tm)
update(v*2, tl, tm, pos, new_val);
else
update(v*2+1, tm+1, tr, pos, new_val);
t[v] = t[v*2] + t[v*2+1];
}
}
Cài đặt hiệu quả bộ nhớ (Memory efficient implementation)¶
Hầu hết mọi người sử dụng cài đặt từ phần trước. Nếu bạn nhìn vào mảng t bạn có thể thấy rằng nó tuân theo việc đánh số các nút cây theo thứ tự duyệt BFS (duyệt theo cấp - level-order traversal).
Sử dụng cách duyệt này, các con của nút $v$ lần lượt là $2v$ và $2v + 1$.
Tuy nhiên, nếu $n$ không phải là lũy thừa của hai, phương pháp này sẽ bỏ qua một số chỉ số và để lại một số phần của mảng t không được sử dụng.
Mức tiêu thụ bộ nhớ bị giới hạn bởi $4n$, mặc dù một Segment Tree của một mảng $n$ phần tử chỉ yêu cầu $2n - 1$ nút.
Tuy nhiên nó có thể giảm được. Chúng ta đánh số lại các nút của cây theo thứ tự duyệt Euler tour (duyệt tiền thứ tự - pre-order traversal), và chúng ta viết tất cả các nút này cạnh nhau.
Hãy xem xét một nút tại chỉ số $v$, và để nó quản lý đoạn $[l, r]$, và đặt $mid = \dfrac{l + r}{2}$. Rõ ràng là con trái sẽ có chỉ số $v + 1$. Con trái quản lý đoạn $[l, mid]$, tức là tổng cộng sẽ có $2 * (mid - l + 1) - 1$ nút trong cây con của con trái. Do đó, chúng ta có thể tính toán chỉ số của con phải của $v$. Chỉ số sẽ là $v + 2 * (mid - l + 1)$. Bằng cách đánh số này, chúng ta đạt được sự sụt giảm bộ nhớ cần thiết xuống $2n$.
Các phiên bản nâng cao của Segment Trees (Advanced versions of Segment Trees)¶
Một Segment Tree là một cấu trúc dữ liệu rất linh hoạt, và cho phép các biến thể và mở rộng theo nhiều hướng khác nhau. Hãy thử phân loại chúng dưới đây.
Các truy vấn phức tạp hơn (More complex queries)¶
Có thể khá dễ dàng để thay đổi Segment Tree theo một hướng, sao cho nó tính toán các truy vấn khác nhau (ví dụ: tính toán giá trị nhỏ nhất / lớn nhất thay vì tổng), nhưng nó cũng có thể rất không đơn giản.
Tìm giá trị lớn nhất (Finding the maximum)¶
Chúng ta hãy thay đổi nhẹ điều kiện của bài toán được mô tả ở trên: thay vì truy vấn tổng, bây giờ chúng ta sẽ thực hiện các truy vấn giá trị lớn nhất.
Cây sẽ có cấu trúc chính xác giống như cây được mô tả ở trên. Chúng ta chỉ cần thay đổi cách tính $t[v]$ trong các hàm $\text{build}$ và $\text{update}$. $t[v]$ bây giờ sẽ lưu trữ giá trị lớn nhất của đoạn tương ứng. Và chúng ta cũng cần thay đổi việc tính toán giá trị trả về của hàm $\text{sum}$ (thay thế phép cộng bằng giá trị lớn nhất).
Tất nhiên bài toán này có thể dễ dàng thay đổi thành việc tính toán giá trị nhỏ nhất thay vì giá trị lớn nhất.
Thay vì hiển thị một cài đặt cho bài toán này, cài đặt sẽ được đưa ra cho một phiên bản phức tạp hơn của bài toán này trong phần tiếp theo.
Tìm giá trị lớn nhất và số lần xuất hiện của nó (Finding the maximum and the number of times it appears)¶
Nhiệm vụ này rất giống với nhiệm vụ trước. Ngoài việc tìm giá trị lớn nhất, chúng ta cũng phải tìm số lần xuất hiện của nó.
Để giải quyết bài toán này, chúng ta lưu trữ một cặp số tại mỗi nút trong cây: Ngoài giá trị lớn nhất, chúng ta cũng lưu trữ số lần xuất hiện của nó trong đoạn tương ứng. Việc xác định cặp chính xác để lưu trữ tại $t[v]$ vẫn có thể được thực hiện trong thời gian hằng số bằng cách sử dụng thông tin của các cặp được lưu trữ tại các nút con. Việc kết hợp hai cặp như vậy nên được thực hiện trong một hàm riêng biệt, vì đây sẽ là một thao tác mà chúng ta sẽ làm trong khi xây dựng cây, trong khi trả lời các truy vấn giá trị lớn nhất và trong khi thực hiện các sửa đổi.
pair<int, int> t[4*MAXN];
pair<int, int> combine(pair<int, int> a, pair<int, int> b) {
if (a.first > b.first)
return a;
if (b.first > a.first)
return b;
return make_pair(a.first, a.second + b.second);
}
void build(int a[], int v, int tl, int tr) {
if (tl == tr) {
t[v] = make_pair(a[tl], 1);
} else {
int tm = (tl + tr) / 2;
build(a, v*2, tl, tm);
build(a, v*2+1, tm+1, tr);
t[v] = combine(t[v*2], t[v*2+1]);
}
}
pair<int, int> get_max(int v, int tl, int tr, int l, int r) {
if (l > r)
return make_pair(-INF, 0);
if (l == tl && r == tr)
return t[v];
int tm = (tl + tr) / 2;
return combine(get_max(v*2, tl, tm, l, min(r, tm)),
get_max(v*2+1, tm+1, tr, max(l, tm+1), r));
}
void update(int v, int tl, int tr, int pos, int new_val) {
if (tl == tr) {
t[v] = make_pair(new_val, 1);
} else {
int tm = (tl + tr) / 2;
if (pos <= tm)
update(v*2, tl, tm, pos, new_val);
else
update(v*2+1, tm+1, tr, pos, new_val);
t[v] = combine(t[v*2], t[v*2+1]);
}
}
Tính ước chung lớn nhất / bội chung nhỏ nhất (Compute the greatest common divisor / least common multiple)¶
Trong bài toán này, chúng ta muốn tính GCD / LCM của tất cả các số trong các phạm vi đã cho của mảng.
Biến thể thú vị này của Segment Tree có thể được giải quyết theo cách chính xác giống như các Segment Trees mà chúng ta đã suy ra cho các truy vấn tổng / giá trị nhỏ nhất / giá trị lớn nhất: chỉ cần lưu trữ GCD / LCM của nút tương ứng trong mỗi nút của cây. Việc kết hợp hai nút có thể được thực hiện bằng cách tính GCD / LCM của cả hai nút.
Đếm số lượng số 0, tìm số 0 thứ $k$ (Counting the number of zeros, searching for the k-th zero)¶
Trong bài toán này, chúng ta muốn tìm số lượng số 0 trong một đoạn đã cho, và tìm thêm chỉ số của số 0 thứ $k$ bằng cách sử dụng một hàm thứ hai.
Một lần nữa, chúng ta phải thay đổi các giá trị lưu trữ của cây một chút: Lần này chúng ta sẽ lưu trữ số lượng số 0 trong mỗi đoạn trong $t[]$. Khá rõ ràng về cách cài đặt các hàm $\text{build}$, $\text{update}$ và $\text{count_zero}$, chúng ta chỉ cần sử dụng các ý tưởng từ bài toán truy vấn tổng. Do đó, chúng ta đã giải quyết phần đầu tiên của bài toán.
Bây giờ chúng ta học cách giải quyết bài toán tìm số 0 thứ $k$ trong mảng $a[]$. Để thực hiện nhiệm vụ này, chúng ta sẽ đi xuống Segment Tree, bắt đầu từ nút gốc, và di chuyển mỗi lần sang con trái hoặc con phải, tùy thuộc vào việc đoạn nào chứa số 0 thứ $k$. Để quyết định chúng ta cần đi đến con nào, chỉ cần nhìn vào số lượng số 0 xuất hiện trong đoạn tương ứng với nút trái. Nếu số đếm đã tính toán trước này lớn hơn hoặc bằng $k$, cần phải đi xuống con trái, và ngược lại đi xuống con phải. Lưu ý, nếu chúng ta chọn con phải, chúng ta phải trừ số lượng số 0 của con trái khỏi $k$.
Trong việc cài đặt, chúng ta có thể xử lý trường hợp đặc biệt, $a[]$ chứa ít hơn $k$ số 0, bằng cách trả về -1.
int find_kth(int v, int tl, int tr, int k) {
if (k > t[v])
return -1;
if (tl == tr)
return tl;
int tm = (tl + tr) / 2;
if (t[v*2] >= k)
return find_kth(v*2, tl, tm, k);
else
return find_kth(v*2+1, tm+1, tr, k - t[v*2]);
}
Tìm kiếm tiền tố mảng với một lượng nhất định (Searching for an array prefix with a given amount)¶
Nhiệm vụ như sau: đối với một giá trị $x$ đã cho, chúng ta phải nhanh chóng tìm chỉ số nhỏ nhất $i$ sao cho tổng của $i$ phần tử đầu tiên của mảng $a[]$ lớn hơn hoặc bằng $x$ (giả sử rằng mảng $a[]$ chỉ chứa các giá trị không âm).
Nhiệm vụ này có thể được giải quyết bằng cách sử dụng tìm kiếm nhị phân, tính tổng của các tiền tố bằng Segment Tree. Tuy nhiên điều này sẽ dẫn đến một giải pháp $O(\log^2 n)$.
Thay vào đó, chúng ta có thể sử dụng cùng một ý tưởng như trong phần trước, và tìm vị trí bằng cách đi xuống cây: bằng cách di chuyển mỗi lần sang trái hoặc phải, tùy thuộc vào tổng của con trái. Do đó tìm thấy câu trả lời trong thời gian $O(\log n)$.
Tìm kiếm phần tử đầu tiên lớn hơn một lượng nhất định (Searching for the first element greater than a given amount)¶
Nhiệm vụ như sau: đối với một giá trị $x$ đã cho và một đoạn $a[l \dots r]$, tìm $i$ nhỏ nhất trong đoạn $a[l \dots r]$, sao cho $a[i]$ lớn hơn $x$.
Nhiệm vụ này có thể được giải quyết bằng cách sử dụng tìm kiếm nhị phân trên các truy vấn tiền tố max với Segment Tree. Tuy nhiên, điều này sẽ dẫn đến một giải pháp $O(\log^2 n)$.
Thay vào đó, chúng ta có thể sử dụng cùng một ý tưởng như trong các phần trước, và tìm vị trí bằng cách đi xuống cây: bằng cách di chuyển mỗi lần sang trái hoặc phải, tùy thuộc vào giá trị lớn nhất của con trái. Do đó tìm thấy câu trả lời trong thời gian $O(\log n)$.
int get_first(int v, int tl, int tr, int l, int r, int x) {
if(tl > r || tr < l) return -1;
if(t[v] <= x) return -1;
if (tl== tr) return tl;
int tm = tl + (tr-tl)/2;
int left = get_first(2*v, tl, tm, l, r, x);
if(left != -1) return left;
return get_first(2*v+1, tm+1, tr, l ,r, x);
}
Tìm các đoạn con có tổng lớn nhất (Finding subsegments with the maximal sum)¶
Ở đây một lần nữa chúng ta nhận được một đoạn $a[l \dots r]$ cho mỗi truy vấn, lần này chúng ta phải tìm một đoạn con $a[l^\prime \dots r^\prime]$ sao cho $l \le l^\prime$ và $r^\prime \le r$ và tổng của các phần tử của đoạn này là lớn nhất. Như trước đây chúng ta cũng muốn có thể sửa đổi các phần tử riêng lẻ của mảng. Các phần tử của mảng có thể là số âm, và đoạn con tối ưu có thể rỗng (ví dụ: nếu tất cả các phần tử đều âm).
Bài toán này là một cách sử dụng không đơn giản của Segment Tree. Lần này chúng ta sẽ lưu trữ bốn giá trị cho mỗi nút: tổng của đoạn, tổng tiền tố lớn nhất, tổng hậu tố lớn nhất, và tổng của đoạn con lớn nhất trong nó. Nói cách khác, đối với mỗi đoạn của Segment Tree, câu trả lời đã được tính toán trước cũng như các câu trả lời cho các đoạn chạm vào ranh giới bên trái và bên phải của đoạn.
Làm thế nào để xây dựng một cái cây với dữ liệu như vậy? Một lần nữa chúng ta tính toán nó theo kiểu đệ quy: đầu tiên chúng ta tính toán tất cả bốn giá trị cho con trái và con phải, và sau đó kết hợp chúng để lưu trữ bốn giá trị cho nút hiện tại. Lưu ý câu trả lời cho nút hiện tại là một trong số:
- câu trả lời của con trái, có nghĩa là đoạn con tối ưu nằm hoàn toàn trong đoạn của con trái
- câu trả lời của con phải, có nghĩa là đoạn con tối ưu nằm hoàn toàn trong đoạn của con phải
- tổng của tổng hậu tố lớn nhất của con trái và tổng tiền tố lớn nhất của con phải, có nghĩa là đoạn con tối ưu giao với cả hai con.
Do đó câu trả lời cho nút hiện tại là giá trị lớn nhất của ba giá trị này. Việc tính toán tổng tiền tố / hậu tố lớn nhất thậm chí còn dễ dàng hơn. Dưới đây là cài đặt của hàm $\text{combine}$, chỉ nhận dữ liệu từ con trái và con phải, và trả về dữ liệu của nút hiện tại.
struct data {
int sum, pref, suff, ans;
};
data combine(data l, data r) {
data res;
res.sum = l.sum + r.sum;
res.pref = max(l.pref, l.sum + r.pref);
res.suff = max(r.suff, r.sum + l.suff);
res.ans = max(max(l.ans, r.ans), l.suff + r.pref);
return res;
}
Sử dụng hàm $\text{combine}$, thật dễ dàng để xây dựng Segment Tree. Chúng ta có thể cài đặt nó theo cách chính xác giống như trong các cài đặt trước. Để khởi tạo các nút lá, chúng ta tạo thêm hàm phụ trợ $\text{make_data}$, sẽ trả về một đối tượng $\text{data}$ chứa thông tin của một giá trị duy nhất.
data make_data(int val) {
data res;
res.sum = val;
res.pref = res.suff = res.ans = max(0, val);
return res;
}
void build(int a[], int v, int tl, int tr) {
if (tl == tr) {
t[v] = make_data(a[tl]);
} else {
int tm = (tl + tr) / 2;
build(a, v*2, tl, tm);
build(a, v*2+1, tm+1, tr);
t[v] = combine(t[v*2], t[v*2+1]);
}
}
void update(int v, int tl, int tr, int pos, int new_val) {
if (tl == tr) {
t[v] = make_data(new_val);
} else {
int tm = (tl + tr) / 2;
if (pos <= tm)
update(v*2, tl, tm, pos, new_val);
else
update(v*2+1, tm+1, tr, pos, new_val);
t[v] = combine(t[v*2], t[v*2+1]);
}
}
Chỉ còn lại, làm thế nào để tính toán câu trả lời cho một truy vấn. Để trả lời nó, chúng ta đi xuống cây như trước, chia truy vấn thành nhiều đoạn con trùng với các đoạn của Segment Tree, và kết hợp các câu trả lời trong chúng thành một câu trả lời duy nhất cho truy vấn. Khi đó, rõ ràng là công việc hoàn toàn giống như trong Segment Tree đơn giản, nhưng thay vì tính tổng / tối thiểu / tối đa các giá trị, chúng ta sử dụng hàm $\text{combine}$.
data query(int v, int tl, int tr, int l, int r) {
if (l > r)
return make_data(0);
if (l == tl && r == tr)
return t[v];
int tm = (tl + tr) / 2;
return combine(query(v*2, tl, tm, l, min(r, tm)),
query(v*2+1, tm+1, tr, max(l, tm+1), r));
}
Lưu trữ toàn bộ mảng con trong mỗi nút (Saving the entire subarrays in each vertex)¶
Đây là một tiểu mục riêng biệt đứng tách biệt với những cái khác, bởi vì tại mỗi nút của Segment Tree, chúng ta không lưu trữ thông tin về đoạn tương ứng ở dạng nén (tổng, tối thiểu, tối đa, ...), mà lưu trữ tất cả các phần tử của đoạn. Do đó, gốc của Segment Tree sẽ lưu trữ tất cả các phần tử của mảng, nút con bên trái sẽ lưu trữ nửa đầu của mảng, nút bên phải nửa sau, v.v.
Trong ứng dụng đơn giản nhất của kỹ thuật này, chúng ta lưu trữ các phần tử theo thứ tự đã sắp xếp. Trong các phiên bản phức tạp hơn, các phần tử không được lưu trữ trong danh sách, mà là các cấu trúc dữ liệu nâng cao hơn (sets, maps, ...). Nhưng tất cả các phương pháp này đều có yếu tố chung, đó là mỗi nút yêu cầu bộ nhớ tuyến tính (tức là tỷ lệ thuận với độ dài của đoạn tương ứng).
Câu hỏi tự nhiên đầu tiên, khi xem xét các Segment Trees này, là về mức tiêu thụ bộ nhớ. Theo trực giác, điều này có thể trông giống như bộ nhớ $O(n^2)$, nhưng hóa ra toàn bộ cây sẽ chỉ cần bộ nhớ $O(n \log n)$. Tại sao lại như vậy? Khá đơn giản, bởi vì mỗi phần tử của mảng rơi vào $O(\log n)$ đoạn (hãy nhớ chiều cao của cây là $O(\log n)$).
Vì vậy, mặc dù có vẻ phung phí của một Segment Tree như vậy, nó chỉ tiêu thụ nhiều bộ nhớ hơn một chút so với Segment Tree thông thường.
Một số ứng dụng điển hình của cấu trúc dữ liệu này được mô tả dưới đây. Điều đáng chú ý là sự tương đồng của các Segment Trees này với cấu trúc dữ liệu 2D (trên thực tế đây là cấu trúc dữ liệu 2D, nhưng với khả năng hạn chế).
Tìm số nhỏ nhất lớn hơn hoặc bằng một số đã chỉ định. Không có truy vấn sửa đổi.¶
Chúng ta muốn trả lời các truy vấn có dạng sau: đối với ba số đã cho $(l, r, x)$, chúng ta phải tìm số nhỏ nhất trong đoạn $a[l \dots r]$ lớn hơn hoặc bằng $x$.
Chúng ta xây dựng một Segment Tree. Trong mỗi nút, chúng ta lưu trữ một danh sách đã sắp xếp của tất cả các số xuất hiện trong đoạn tương ứng, như được mô tả ở trên. Làm thế nào để xây dựng một Segment Tree như vậy hiệu quả nhất có thể? Như mọi khi, chúng ta tiếp cận vấn đề này một cách đệ quy: giả sử danh sách của các con bên trái và bên phải đã được xây dựng, và chúng ta muốn xây dựng danh sách cho nút hiện tại. Từ góc nhìn này, thao tác bây giờ là tầm thường và có thể được thực hiện trong thời gian tuyến tính: Chúng ta chỉ cần kết hợp hai danh sách đã sắp xếp thành một, có thể được thực hiện bằng cách lặp qua chúng bằng hai con trỏ. C++ STL đã có một triển khai của thuật toán này.
Bởi vì cấu trúc này của Segment Tree và những điểm tương đồng với thuật toán sắp xếp trộn (merge sort), cấu trúc dữ liệu này cũng thường được gọi là "Merge Sort Tree".
vector<int> t[4*MAXN];
void build(int a[], int v, int tl, int tr) {
if (tl == tr) {
t[v] = vector<int>(1, a[tl]);
} else {
int tm = (tl + tr) / 2;
build(a, v*2, tl, tm);
build(a, v*2+1, tm+1, tr);
merge(t[v*2].begin(), t[v*2].end(), t[v*2+1].begin(), t[v*2+1].end(),
back_inserter(t[v]));
}
}
Chúng ta đã biết rằng Segment Tree được xây dựng theo cách này sẽ yêu cầu bộ nhớ $O(n \log n)$. Và nhờ triển khai này, việc xây dựng của nó cũng mất thời gian $O(n \log n)$, suy cho cùng, mỗi danh sách được xây dựng trong thời gian tuyến tính đối với kích thước của nó.
Bây giờ hãy xem xét câu trả lời cho truy vấn. Chúng ta sẽ đi xuống cây, giống như trong Segment Tree thông thường, chia đoạn $a[l \dots r]$ của chúng ta thành nhiều đoạn con (thành tối đa $O(\log n)$ phần). Rõ ràng là câu trả lời của toàn bộ câu trả lời là giá trị nhỏ nhất của mỗi truy vấn con. Vì vậy, bây giờ chúng ta chỉ cần hiểu, làm thế nào để phản hồi một truy vấn trên một đoạn con như vậy tương ứng với một số nút của cây.
Chúng ta đang ở một nút nào đó của Segment Tree và chúng ta muốn tính toán câu trả lời cho truy vấn, tức là tìm số nhỏ nhất lớn hơn hoặc bằng một số $x$ đã cho. Vì nút chứa danh sách các phần tử theo thứ tự đã sắp xếp, chúng ta có thể chỉ cần thực hiện tìm kiếm nhị phân trên danh sách này và trả về số đầu tiên, lớn hơn hoặc bằng $x$.
Do đó, câu trả lời cho truy vấn trong một đoạn của cây mất thời gian $O(\log n)$, và toàn bộ truy vấn được xử lý trong $O(\log^2 n)$.
int query(int v, int tl, int tr, int l, int r, int x) {
if (l > r)
return INF;
if (l == tl && r == tr) {
vector<int>::iterator pos = lower_bound(t[v].begin(), t[v].end(), x);
if (pos != t[v].end())
return *pos;
return INF;
}
int tm = (tl + tr) / 2;
return min(query(v*2, tl, tm, l, min(r, tm), x),
query(v*2+1, tm+1, tr, max(l, tm+1), r, x));
}
Hằng số $\text{INF}$ bằng một số lớn nào đó lớn hơn tất cả các số trong mảng. Việc sử dụng nó có nghĩa là, không có số nào lớn hơn hoặc bằng $x$ trong đoạn. Nó có ý nghĩa là "không có câu trả lời trong khoảng đã cho".
Tìm số nhỏ nhất lớn hơn hoặc bằng một số đã chỉ định. Với các truy vấn sửa đổi.¶
Nhiệm vụ này tương tự như trước. Cách tiếp cận cuối cùng có một nhược điểm, đó là không thể sửa đổi mảng giữa các lần trả lời truy vấn. Bây giờ chúng ta muốn làm chính xác điều này: một truy vấn sửa đổi sẽ thực hiện phép gán $a[i] = y$.
Giải pháp tương tự như giải pháp của vấn đề trước, nhưng thay vì danh sách tại mỗi nút của Segment Tree, chúng ta sẽ lưu trữ một danh sách cân bằng cho phép bạn tìm kiếm nhanh các số, xóa số và chèn số mới. Vì mảng có thể chứa một số lặp lại, lựa chọn tối ưu là cấu trúc dữ liệu $\text{multiset}$.
Việc xây dựng một Segment Tree như vậy được thực hiện theo cách khá giống như trong vấn đề trước, chỉ có điều bây giờ chúng ta cần kết hợp các $\text{multiset}$ chứ không phải danh sách đã sắp xếp. Điều này dẫn đến thời gian xây dựng là $O(n \log^2 n)$ (nói chung việc hợp nhất hai cây đỏ-đen có thể được thực hiện trong thời gian tuyến tính, nhưng C++ STL không đảm bảo độ phức tạp thời gian này).
Hàm $\text{query}$ cũng gần như tương đương, chỉ khác là hàm $\text{lower_bound}$ của hàm $\text{multiset}$ nên được gọi thay thế ($\text{std::lower_bound}$ chỉ hoạt động trong thời gian $O(\log n)$ nếu được sử dụng với các trình lặp truy cập ngẫu nhiên).
Cuối cùng là yêu cầu sửa đổi. Để xử lý nó, chúng ta phải đi xuống cây, và sửa đổi tất cả $\text{multiset}$ từ các đoạn tương ứng có chứa phần tử bị ảnh hưởng. Chúng ta chỉ cần xóa giá trị cũ của phần tử này (nhưng chỉ một lần xuất hiện), và chèn giá trị mới.
void update(int v, int tl, int tr, int pos, int new_val) {
t[v].erase(t[v].find(a[pos]));
t[v].insert(new_val);
if (tl != tr) {
int tm = (tl + tr) / 2;
if (pos <= tm)
update(v*2, tl, tm, pos, new_val);
else
update(v*2+1, tm+1, tr, pos, new_val);
} else {
a[pos] = new_val;
}
}
Việc xử lý truy vấn sửa đổi này cũng mất thời gian $O(\log^2 n)$.
Tìm số nhỏ nhất lớn hơn hoặc bằng một số đã chỉ định. Tăng tốc với "fractional cascading".¶
Chúng ta có cùng một phát biểu bài toán, chúng ta muốn tìm số nhỏ nhất lớn hơn hoặc bằng $x$ trong một đoạn, nhưng lần này trong thời gian $O(\log n)$. Chúng ta sẽ cải thiện độ phức tạp thời gian bằng cách sử dụng kỹ thuật "fractional cascading".
Fractional cascading là một kỹ thuật đơn giản cho phép bạn cải thiện thời gian chạy của nhiều tìm kiếm nhị phân, được thực hiện cùng một lúc. Cách tiếp cận trước đây của chúng ta đối với truy vấn tìm kiếm là, chúng ta chia nhiệm vụ thành nhiều nhiệm vụ con, mỗi nhiệm vụ được giải quyết bằng một tìm kiếm nhị phân. Fractional cascading cho phép bạn thay thế tất cả các tìm kiếm nhị phân này bằng một tìm kiếm duy nhất.
Ví dụ đơn giản nhất và rõ ràng nhất về fractional cascading là bài toán sau: có $k$ danh sách số đã sắp xếp, và chúng ta phải tìm trong mỗi danh sách số đầu tiên lớn hơn hoặc bằng số đã cho.
Thay vì thực hiện tìm kiếm nhị phân cho mỗi danh sách, chúng ta có thể hợp nhất tất cả các danh sách thành một danh sách lớn đã sắp xếp. Ngoài ra, đối với mỗi phần tử $y$, chúng ta lưu trữ một danh sách kết quả tìm kiếm $y$ trong mỗi danh sách trong số $k$ danh sách. Do đó nếu chúng ta muốn tìm số nhỏ nhất lớn hơn hoặc bằng $x$, chúng ta chỉ cần thực hiện một tìm kiếm nhị phân duy nhất, và từ danh sách các chỉ số, chúng ta có thể xác định số nhỏ nhất trong mỗi danh sách. Tuy nhiên, cách tiếp cận này yêu cầu $O(n \cdot k)$ ($n$ là độ dài của các danh sách kết hợp), có thể khá kém hiệu quả.
Fractional cascading làm giảm độ phức tạp bộ nhớ này xuống $O(n)$ bộ nhớ, bằng cách tạo từ $k$ danh sách đầu vào $k$ danh sách mới, trong đó mỗi danh sách chứa danh sách tương ứng và thêm vào đó là mỗi phần tử thứ hai của danh sách mới tiếp theo. Sử dụng cấu trúc này, chỉ cần lưu trữ hai chỉ số, chỉ số của phần tử trong danh sách gốc, và chỉ số của phần tử trong danh sách mới tiếp theo. Vì vậy, cách tiếp cận này chỉ sử dụng $O(n)$ bộ nhớ, và vẫn có thể trả lời các truy vấn bằng cách sử dụng một tìm kiếm nhị phân duy nhất.
Nhưng đối với ứng dụng của chúng ta, chúng ta không cần toàn bộ sức mạnh của fractional cascading. Trong Segment Tree của chúng ta, một nút sẽ chứa danh sách đã sắp xếp của tất cả các phần tử xuất hiện trong các cây con bên trái hoặc bên phải (giống như trong Merge Sort Tree). Ngoài danh sách đã sắp xếp này, chúng ta lưu trữ hai vị trí cho mỗi phần tử. Đối với một phần tử $y$, chúng ta lưu trữ chỉ số nhỏ nhất $i$, sao cho phần tử thứ $i$ trong danh sách đã sắp xếp của con trái lớn hơn hoặc bằng $y$. Và chúng ta lưu trữ chỉ số nhỏ nhất $j$, sao cho phần tử thứ $j$ trong danh sách đã sắp xếp của con phải lớn hơn hoặc bằng $y$. Các giá trị này có thể được tính toán song song với bước hợp nhất khi chúng ta xây dựng cây.
Điều này tăng tốc các truy vấn như thế nào?
Hãy nhớ rằng, trong giải pháp thông thường, chúng ta đã thực hiện tìm kiếm nhị phân trong mọi nút. Nhưng với sửa đổi này, chúng ta có thể tránh tất cả ngoại trừ một cái.
Để trả lời một truy vấn, chúng ta chỉ cần thực hiện tìm kiếm nhị phân trong nút gốc. Điều này cho chúng ta phần tử nhỏ nhất $y \ge x$ trong mảng hoàn chỉnh, nhưng nó cũng cho chúng ta hai vị trí. Chỉ số của phần tử nhỏ nhất lớn hơn hoặc bằng $x$ trong cây con trái, và chỉ số của phần tử nhỏ nhất $y$ trong cây con phải. Lưu ý rằng $\ge y$ giống như $\ge x$, vì mảng của chúng ta không chứa bất kỳ phần tử nào giữa $x$ và $y$. Trong giải pháp Merge Sort Tree thông thường, chúng ta sẽ tính toán các chỉ số này thông qua tìm kiếm nhị phân, nhưng với sự trợ giúp của các giá trị đã tính toán trước, chúng ta chỉ có thể tra cứu chúng trong $O(1)$. Và chúng ta có thể lặp lại điều đó cho đến khi chúng ta truy cập tất cả các nút bao gồm khoảng truy vấn của chúng ta.
Tóm lại, như thường lệ, chúng ta chạm vào $O(\log n)$ nút trong một truy vấn. Trong nút gốc, chúng ta thực hiện tìm kiếm nhị phân, và trong tất cả các nút khác, chúng ta chỉ thực hiện công việc hằng số. Điều này có nghĩa là độ phức tạp để trả lời một truy vấn là $O(\log n)$.
Nhưng hãy chú ý rằng, điều này sử dụng bộ nhớ gấp ba lần so với Merge Sort Tree thông thường, vốn đã sử dụng rất nhiều bộ nhớ ($O(n \log n)$).
Rất đơn giản để áp dụng kỹ thuật này cho một vấn đề, không yêu cầu bất kỳ truy vấn sửa đổi nào. Hai vị trí chỉ là các số nguyên và có thể dễ dàng được tính toán bằng cách đếm khi hợp nhất hai chuỗi đã sắp xếp.
Vẫn có thể cho phép các truy vấn sửa đổi, nhưng điều đó làm phức tạp toàn bộ mã.
Thay vì số nguyên, bạn cần lưu trữ mảng đã sắp xếp dưới dạng multiset, và thay vì chỉ số, bạn cần lưu trữ trình lặp (iterators).
Và bạn cần làm việc rất cẩn thận, để bạn tăng hoặc giảm đúng các trình lặp trong một truy vấn sửa đổi.
Các biến thể có thể khác (Other possible variations)¶
kỹ thuật này ngụ ý một lớp hoàn toàn mới các ứng dụng có thể. Thay vì lưu trữ một $\text{vector}$ hoặc một $\text{multiset}$ trong mỗi nút, các cấu trúc dữ liệu khác có thể được sử dụng: các Segment Trees khác (phần nào được thảo luận trong Khái quát hóa sang các chiều cao hơn), Fenwick Trees, Cartesian trees, v.v.
Cập nhật đoạn (Lazy Propagation)¶
Tất cả các bài toán trong các phần trên đã thảo luận về các truy vấn sửa đổi chỉ ảnh hưởng đến một phần tử duy nhất của mảng mỗi lần. Tuy nhiên, Segment Tree cho phép áp dụng các truy vấn sửa đổi cho toàn bộ một đoạn các phần tử liền kề, và thực hiện truy vấn trong cùng thời gian $O(\log n)$.
Cộng trên các đoạn (Addition on segments)¶
Chúng ta bắt đầu bằng cách xem xét các bài toán có dạng đơn giản nhất: truy vấn sửa đổi nên cộng một số $x$ vào tất cả các số trong đoạn $a[l \dots r]$. Truy vấn thứ hai, mà chúng ta phải trả lời, chỉ đơn giản là yêu cầu giá trị của $a[i]$.
Để làm cho truy vấn cộng hiệu quả, chúng ta lưu trữ tại mỗi nút trong Segment Tree số lượng chúng ta nên cộng vào tất cả các số trong đoạn tương ứng. Ví dụ, nếu truy vấn "cộng 3 vào toàn bộ mảng $a[0 \dots n-1]$" đến, thì chúng ta đặt số 3 vào gốc của cây. Nói chung, chúng ta phải đặt số này vào nhiều đoạn, tạo thành một phân vùng của đoạn truy vấn. Do đó, chúng ta không phải thay đổi tất cả $O(n)$ giá trị, mà chỉ $O(\log n)$.
Thế nên bây giờ nếu có một truy vấn hỏi giá trị hiện tại của một mục mảng cụ thể, chỉ cần đi xuống cây và cộng tất cả các giá trị tìm thấy trên đường đi.
void build(int a[], int v, int tl, int tr) {
if (tl == tr) {
t[v] = a[tl];
} else {
int tm = (tl + tr) / 2;
build(a, v*2, tl, tm);
build(a, v*2+1, tm+1, tr);
t[v] = 0;
}
}
void update(int v, int tl, int tr, int l, int r, int add) {
if (l > r)
return;
if (l == tl && r == tr) {
t[v] += add;
} else {
int tm = (tl + tr) / 2;
update(v*2, tl, tm, l, min(r, tm), add);
update(v*2+1, tm+1, tr, max(l, tm+1), r, add);
}
}
int get(int v, int tl, int tr, int pos) {
if (tl == tr)
return t[v];
int tm = (tl + tr) / 2;
if (pos <= tm)
return t[v] + get(v*2, tl, tm, pos);
else
return t[v] + get(v*2+1, tm+1, tr, pos);
}
Gán trên các đoạn (Assignment on segments)¶
Bây giờ giả sử rằng truy vấn sửa đổi yêu cầu gán mỗi phần tử của một đoạn nhất định $a[l \dots r]$ cho một giá trị $p$ nào đó. Là một truy vấn thứ hai, chúng ta sẽ xem xét lại việc đọc giá trị của mảng $a[i]$.
Để thực hiện truy vấn sửa đổi này trên toàn bộ đoạn, bạn phải lưu trữ tại mỗi nút của Segment Tree xem đoạn tương ứng có được bao phủ hoàn toàn bởi cùng một giá trị hay không. Điều này cho phép chúng ta thực hiện cập nhật "lười biếng" (lazy): thay vì thay đổi tất cả các đoạn trong cây bao phủ đoạn truy vấn, chúng ta chỉ thay đổi một số, và để những cái khác không thay đổi. Một nút được đánh dấu sẽ có nghĩa là, mọi phần tử của đoạn tương ứng được gán cho giá trị đó, và thực tế là toàn bộ cây con cũng chỉ nên chứa giá trị này. Theo một nghĩa nào đó, chúng ta lười biếng và trì hoãn việc viết giá trị mới cho tất cả các nút đó. Chúng ta có thể làm công việc tẻ nhạt này sau, nếu điều này là cần thiết.
Vì vậy, sau khi truy vấn sửa đổi được thực thi, một số phần của cây trở nên không liên quan - một số sửa đổi vẫn chưa được thực hiện trong đó.
Ví dụ nếu một truy vấn sửa đổi "gán một số cho toàn bộ mảng $a[0 \dots n-1]$" được thực thi, trong Segment Tree chỉ có một thay đổi duy nhất được thực hiện - số được đặt vào gốc của cây và nút này được đánh dấu. Các đoạn còn lại không thay đổi, mặc dù trên thực tế số này nên được đặt trong toàn bộ cây.
Bây giờ giả sử rằng truy vấn sửa đổi thứ hai nói rằng, nửa đầu của mảng $a[0 \dots n/2]$ nên được gán bằng một số khác. Để xử lý truy vấn này, chúng ta phải gán mỗi phần tử trong toàn bộ con trái của nút gốc bằng số đó. Nhưng trước khi chúng ta làm điều này, trước tiên chúng ta phải giải quyết nút gốc. Sự tinh tế ở đây là nửa bên phải của mảng vẫn nên được gán cho giá trị của truy vấn đầu tiên, và tại thời điểm hiện tại không có thông tin nào cho nửa bên phải được lưu trữ.
Cách để giải quyết vấn đề này là đẩy (push) thông tin của gốc xuống các con của nó, tức là nếu gốc của cây được gán bằng bất kỳ số nào, thì chúng ta gán các nút con trái và phải bằng số này và loại bỏ đánh dấu của gốc. Sau đó, chúng ta có thể gán con trái với giá trị mới mà không làm mất bất kỳ thông tin cần thiết nào.
Tóm lại chúng ta nhận được: đối với bất kỳ truy vấn nào (một sửa đổi hoặc truy vấn đọc) trong quá trình đi xuống dọc theo cây, chúng ta phải luôn đẩy thông tin từ nút hiện tại vào cả hai con của nó. Chúng ta có thể hiểu điều này theo cách như vậy, rằng khi chúng ta đi xuống cây, chúng ta áp dụng các sửa đổi bị trì hoãn, nhưng chính xác nhiều nhất mức cần thiết (để không làm giảm độ phức tạp của $O(\log n)$).
Đối với việc cài đặt, chúng ta cần tạo một hàm $\text{push}$, sẽ nhận nút hiện tại, và nó sẽ đẩy thông tin cho nút của nó đến cả hai con của nó. Chúng ta sẽ gọi hàm này ở đầu các hàm truy vấn (nhưng chúng ta sẽ không gọi nó từ các lá, vì không cần đẩy thông tin từ chúng đi xa hơn).
void push(int v) {
if (marked[v]) {
t[v*2] = t[v*2+1] = t[v];
marked[v*2] = marked[v*2+1] = true;
marked[v] = false;
}
}
void update(int v, int tl, int tr, int l, int r, int new_val) {
if (l > r)
return;
if (l == tl && tr == r) {
t[v] = new_val;
marked[v] = true;
} else {
push(v);
int tm = (tl + tr) / 2;
update(v*2, tl, tm, l, min(r, tm), new_val);
update(v*2+1, tm+1, tr, max(l, tm+1), r, new_val);
}
}
int get(int v, int tl, int tr, int pos) {
if (tl == tr) {
return t[v];
}
push(v);
int tm = (tl + tr) / 2;
if (pos <= tm)
return get(v*2, tl, tm, pos);
else
return get(v*2+1, tm+1, tr, pos);
}
Lưu ý: hàm $\text{get}$ cũng có thể được cài đặt theo một cách khác: không thực hiện các cập nhật bị trì hoãn, mà trả về ngay giá trị $t[v]$ nếu $marked[v]$ là đúng.
Cộng trên các đoạn, truy vấn giá trị lớn nhất (Adding on segments, querying for maximum)¶
Bây giờ truy vấn sửa đổi là cộng một số vào tất cả các phần tử trong một đoạn, và truy vấn đọc là tìm giá trị lớn nhất trong một đoạn.
Vì vậy, đối với mỗi nút của Segment Tree, chúng ta phải lưu trữ giá trị lớn nhất của đoạn con tương ứng. Phần thú vị là làm thế nào để tính toán lại các giá trị này trong một yêu cầu sửa đổi.
Vì mục đích này, chúng ta lưu trữ thêm một giá trị bổ sung cho mỗi nút. Trong giá trị này, chúng ta lưu trữ các số hạng mà chúng ta chưa lan truyền đến các nút con. Trước khi di chuyển đến một nút con, chúng ta gọi $\text{push}$ và lan truyền giá trị cho cả hai con. Chúng ta phải làm điều này trong cả hàm $\text{update}$ và hàm $\text{query}$.
void build(int a[], int v, int tl, int tr) {
if (tl == tr) {
t[v] = a[tl];
} else {
int tm = (tl + tr) / 2;
build(a, v*2, tl, tm);
build(a, v*2+1, tm+1, tr);
t[v] = max(t[v*2], t[v*2 + 1]);
}
}
void push(int v) {
t[v*2] += lazy[v];
lazy[v*2] += lazy[v];
t[v*2+1] += lazy[v];
lazy[v*2+1] += lazy[v];
lazy[v] = 0;
}
void update(int v, int tl, int tr, int l, int r, int addend) {
if (l > r)
return;
if (l == tl && tr == r) {
t[v] += addend;
lazy[v] += addend;
} else {
push(v);
int tm = (tl + tr) / 2;
update(v*2, tl, tm, l, min(r, tm), addend);
update(v*2+1, tm+1, tr, max(l, tm+1), r, addend);
t[v] = max(t[v*2], t[v*2+1]);
}
}
int query(int v, int tl, int tr, int l, int r) {
if (l > r)
return -INF;
if (l == tl && tr == r)
return t[v];
push(v);
int tm = (tl + tr) / 2;
return max(query(v*2, tl, tm, l, min(r, tm)),
query(v*2+1, tm+1, tr, max(l, tm+1), r));
}
Khái quát hóa sang các chiều cao hơn (Generalization to higher dimensions)¶
Một Segment Tree có thể được khái quát hóa khá tự nhiên sang các chiều cao hơn. Nếu trong trường hợp một chiều, chúng ta chia các chỉ số của mảng thành các đoạn, thì trong trường hợp hai chiều, chúng ta thực hiện một Segment Tree bình thường đối với các chỉ số đầu tiên, và đối với mỗi đoạn, chúng ta xây dựng một Segment Tree bình thường đối với các chỉ số thứ hai.
Segment Tree 2D đơn giản (Simple 2D Segment Tree)¶
Một ma trận $a[0 \dots n-1, 0 \dots m-1]$ được cho, và chúng ta phải tìm tổng (hoặc tối thiểu/tối đa) trên một ma trận con $a[x_1 \dots x_2, y_1 \dots y_2]$, cũng như thực hiện sửa đổi các phần tử ma trận riêng lẻ (tức là các truy vấn có dạng $a[x][y] = p$).
Vì vậy, chúng ta xây dựng một Segment Tree 2D: đầu tiên là Segment Tree sử dụng tọa độ đầu tiên ($x$), sau đó là thứ hai ($y$).
Để làm cho quá trình xây dựng dễ hiểu hơn, bạn có thể quên đi một lúc rằng ma trận là hai chiều, và chỉ để lại tọa độ đầu tiên. Chúng ta sẽ xây dựng một Segment Tree một chiều thông thường chỉ sử dụng tọa độ đầu tiên. Nhưng thay vì lưu trữ một số trong một đoạn, chúng ta lưu trữ một Segment Tree hoàn chỉnh: tức là tại thời điểm này, chúng ta nhớ rằng chúng ta cũng có một tọa độ thứ hai; nhưng vì tại thời điểm này, tọa độ đầu tiên đã được cố định vào một khoảng nào đó $[l \dots r]$, chúng ta thực sự làm việc với một dải như vậy $a[l \dots r, 0 \dots m-1]$ và đối với nó, chúng ta xây dựng một Segment Tree.
Dưới đây là cài đặt của việc xây dựng một Segment Tree 2D. Nó thực sự đại diện cho hai khối riêng biệt: việc xây dựng một Segment Tree dọc theo tọa độ $x$ ($\text{build}_x$), và tọa độ $y$ ($\text{build}_y$). Đối với các nút lá trong $\text{build}_y$, chúng ta phải phân tách hai trường hợp: khi đoạn hiện tại của tọa độ đầu tiên $[tlx \dots trx]$ có độ dài 1, và khi nó có độ dài lớn hơn một. Trong trường hợp đầu tiên, chúng ta chỉ lấy giá trị tương ứng từ ma trận, và trong trường hợp thứ hai, chúng ta có thể kết hợp các giá trị của hai Segment Tree từ con bên trái và bên phải trong tọa độ $x$.
void build_y(int vx, int lx, int rx, int vy, int ly, int ry) {
if (ly == ry) {
if (lx == rx)
t[vx][vy] = a[lx][ly];
else
t[vx][vy] = t[vx*2][vy] + t[vx*2+1][vy];
} else {
int my = (ly + ry) / 2;
build_y(vx, lx, rx, vy*2, ly, my);
build_y(vx, lx, rx, vy*2+1, my+1, ry);
t[vx][vy] = t[vx][vy*2] + t[vx][vy*2+1];
}
}
void build_x(int vx, int lx, int rx) {
if (lx != rx) {
int mx = (lx + rx) / 2;
build_x(vx*2, lx, mx);
build_x(vx*2+1, mx+1, rx);
}
build_y(vx, lx, rx, 1, 0, m-1);
}
Một Segment Tree như vậy vẫn sử dụng một lượng bộ nhớ tuyến tính, nhưng với hằng số lớn hơn: $16 n m$. Rõ ràng là thủ tục được mô tả $\text{build}_x$ cũng hoạt động trong thời gian tuyến tính.
Bây giờ chúng ta chuyển sang xử lý các truy vấn. Chúng ta sẽ trả lời truy vấn hai chiều bằng cùng một nguyên tắc: đầu tiên phá vỡ truy vấn trên tọa độ đầu tiên, và sau đó đối với mỗi nút đạt được, chúng ta gọi Segment Tree tương ứng của tọa độ thứ hai.
int sum_y(int vx, int vy, int tly, int try_, int ly, int ry) {
if (ly > ry)
return 0;
if (ly == tly && try_ == ry)
return t[vx][vy];
int tmy = (tly + try_) / 2;
return sum_y(vx, vy*2, tly, tmy, ly, min(ry, tmy))
+ sum_y(vx, vy*2+1, tmy+1, try_, max(ly, tmy+1), ry);
}
int sum_x(int vx, int tlx, int trx, int lx, int rx, int ly, int ry) {
if (lx > rx)
return 0;
if (lx == tlx && trx == rx)
return sum_y(vx, 1, 0, m-1, ly, ry);
int tmx = (tlx + trx) / 2;
return sum_x(vx*2, tlx, tmx, lx, min(rx, tmx), ly, ry)
+ sum_x(vx*2+1, tmx+1, trx, max(lx, tmx+1), rx, ly, ry);
}
Hàm này hoạt động trong thời gian $O(\log n \log m)$, vì ban đầu nó đi xuống cây ở tọa độ đầu tiên, và đối với mỗi nút được duyệt trong cây, nó thực hiện một truy vấn trong Segment Tree tương ứng dọc theo tọa độ thứ hai.
Cuối cùng chúng ta xem xét truy vấn sửa đổi. Chúng ta muốn học cách sửa đổi Segment Tree theo sự thay đổi giá trị của một phần tử nào đó $a[x][y] = p$. Rõ ràng là, những thay đổi sẽ chỉ xảy ra trong những nút của Segment Tree đầu tiên bao gồm tọa độ $x$ (và số lượng đó sẽ là $O(\log n)$), và đối với các Segment Tree tương ứng với chúng, các thay đổi sẽ chỉ xảy ra tại những nút bao gồm tọa độ $y$ (và số lượng đó sẽ là $O(\log m)$). Do đó, việc cài đặt sẽ không khác nhiều so với trường hợp một chiều, chỉ có điều bây giờ chúng ta đi xuống tọa độ đầu tiên trước, và sau đó là tọa độ thứ hai.
void update_y(int vx, int lx, int rx, int vy, int ly, int ry, int x, int y, int new_val) {
if (ly == ry) {
if (lx == rx)
t[vx][vy] = new_val;
else
t[vx][vy] = t[vx*2][vy] + t[vx*2+1][vy];
} else {
int my = (ly + ry) / 2;
if (y <= my)
update_y(vx, lx, rx, vy*2, ly, my, x, y, new_val);
else
update_y(vx, lx, rx, vy*2+1, my+1, ry, x, y, new_val);
t[vx][vy] = t[vx][vy*2] + t[vx][vy*2+1];
}
}
void update_x(int vx, int lx, int rx, int x, int y, int new_val) {
if (lx != rx) {
int mx = (lx + rx) / 2;
if (x <= mx)
update_x(vx*2, lx, mx, x, y, new_val);
else
update_x(vx*2+1, mx+1, rx, x, y, new_val);
}
update_y(vx, lx, rx, 1, 0, m-1, x, y, new_val);
}
Nén Segment Tree 2D (Compression of 2D Segment Tree)¶
Giả sử bài toán là như sau: có $n$ điểm trên mặt phẳng được cho bởi tọa độ của chúng $(x_i, y_i)$ và các truy vấn có dạng "đếm số lượng điểm nằm trong hình chữ nhật $((x_1, y_1), (x_2, y_2))$". Rõ ràng là trong trường hợp của một bài toán như vậy, việc xây dựng một Segment Tree hai chiều với $O(n^2)$ phần tử trở nên lãng phí một cách vô lý. Hầu hết bộ nhớ này sẽ bị lãng phí, vì mỗi điểm đơn lẻ chỉ có thể đi vào $O(\log n)$ đoạn của cây dọc theo tọa độ đầu tiên, và do đó tổng kích thước "hữu ích" của tất cả các đoạn cây trên tọa độ thứ hai là $O(n \log n)$.
Vì vậy, chúng ta tiến hành như sau: tại mỗi nút của Segment Tree đối với tọa độ đầu tiên, chúng ta lưu trữ một Segment Tree được xây dựng chỉ bởi những tọa độ thứ hai xảy ra trong đoạn hiện tại của tọa độ đầu tiên. Nói cách khác, khi xây dựng một Segment Tree bên trong một nút có chỉ số $vx$ và các ranh giới $tlx$ và $trx$, chúng ta chỉ xem xét những điểm rơi vào khoảng này $x \in [tlx, trx]$, và xây dựng một Segment Tree chỉ sử dụng chúng.
Do đó, chúng ta sẽ đạt được rằng mỗi Segment Tree trên tọa độ thứ hai sẽ chiếm chính xác nhiều bộ nhớ như nó nên. Kết quả là, tổng lượng bộ nhớ sẽ giảm xuống $O(n \log n)$. Chúng ta vẫn có thể trả lời các truy vấn trong thời gian $O(\log^2 n)$, chúng ta chỉ cần thực hiện tìm kiếm nhị phân trên tọa độ thứ hai, nhưng điều này sẽ không làm xấu đi độ phức tạp.
Nhưng các truy vấn sửa đổi sẽ là không thể với cấu trúc này: trên thực tế nếu một điểm mới xuất hiện, chúng ta phải thêm một phần tử mới vào giữa một Segment Tree nào đó dọc theo tọa độ thứ hai, điều này không thể được thực hiện một cách hiệu quả.
Kết luận, chúng ta lưu ý rằng Segment Tree hai chiều được rút gọn theo cách được mô tả trở nên gần như tương đương với việc sửa đổi Segment Tree một chiều (xem Lưu trữ toàn bộ mảng con trong mỗi nút). Đặc biệt, Segment Tree hai chiều chỉ là một trường hợp đặc biệt của việc lưu trữ một mảng con trong mỗi nút của cây. Theo đó, nếu bạn phải từ bỏ Segment Tree hai chiều do không thể thực hiện truy vấn, thì việc thay thế Segment Tree lồng nhau bằng một cấu trúc dữ liệu mạnh hơn, ví dụ như Cartesian tree, là điều hợp lý.
Bảo tồn lịch sử các giá trị của nó (Persistent Segment Tree)¶
Một cấu trúc dữ liệu persistent là một cấu trúc dữ liệu ghi nhớ trạng thái trước đó của nó cho mỗi lần sửa đổi. Điều này cho phép truy cập bất kỳ phiên bản nào của cấu trúc dữ liệu này mà chúng ta quan tâm và thực hiện truy vấn trên đó.
Segment Tree là một cấu trúc dữ liệu có thể được biến thành một cấu trúc dữ liệu persistent một cách hiệu quả (cả về thời gian và mức tiêu thụ bộ nhớ). Chúng ta muốn tránh sao chép toàn bộ cây trước mỗi lần sửa đổi, và chúng ta không muốn mất hành vi thời gian $O(\log n)$ để trả lời các truy vấn đoạn.
Trên thực tế, bất kỳ yêu cầu thay đổi nào trong Segment Tree đều dẫn đến sự thay đổi dữ liệu của chỉ $O(\log n)$ nút dọc theo đường đi bắt đầu từ gốc. Vì vậy, nếu chúng ta lưu trữ Segment Tree bằng cách sử dụng các con trỏ (tức là một nút lưu trữ các con trỏ đến các nút con trái và phải), thì khi thực hiện truy vấn sửa đổi, chúng ta chỉ cần tạo các nút mới thay vì thay đổi các nút có sẵn. Các nút không bị ảnh hưởng bởi truy vấn sửa đổi vẫn có thể được sử dụng bằng cách trỏ các con trỏ đến các nút cũ. Do đó, đối với một truy vấn sửa đổi, $O(\log n)$ nút mới sẽ được tạo, bao gồm một nút gốc mới của Segment Tree, và toàn bộ phiên bản trước đó của cây bắt nguồn từ nút gốc cũ sẽ không thay đổi.
Hãy đưa ra một ví dụ cài đặt cho Segment Tree đơn giản nhất: khi chỉ có một truy vấn yêu cầu tổng, và các truy vấn sửa đổi của các phần tử đơn lẻ.
struct Vertex {
Vertex *l, *r;
int sum;
Vertex(int val) : l(nullptr), r(nullptr), sum(val) {}
Vertex(Vertex *l, Vertex *r) : l(l), r(r), sum(0) {
if (l) sum += l->sum;
if (r) sum += r->sum;
}
};
Vertex* build(int a[], int tl, int tr) {
if (tl == tr)
return new Vertex(a[tl]);
int tm = (tl + tr) / 2;
return new Vertex(build(a, tl, tm), build(a, tm+1, tr));
}
int get_sum(Vertex* v, int tl, int tr, int l, int r) {
if (l > r)
return 0;
if (l == tl && tr == r)
return v->sum;
int tm = (tl + tr) / 2;
return get_sum(v->l, tl, tm, l, min(r, tm))
+ get_sum(v->r, tm+1, tr, max(l, tm+1), r);
}
Vertex* update(Vertex* v, int tl, int tr, int pos, int new_val) {
if (tl == tr)
return new Vertex(new_val);
int tm = (tl + tr) / 2;
if (pos <= tm)
return new Vertex(update(v->l, tl, tm, pos, new_val), v->r);
else
return new Vertex(v->l, update(v->r, tm+1, tr, pos, new_val));
}
Với cách tiếp cận được mô tả ở trên, hầu hết mọi Segment Tree đều có thể được biến thành một cấu trúc dữ liệu persistent.
Tìm số nhỏ thứ $k$ trong một đoạn (Finding the $k$-th smallest number in a range)¶
Lần này chúng ta phải trả lời các truy vấn có dạng "Phần tử nhỏ thứ $k$ trong đoạn $a[l \dots r]$ là gì". Truy vấn này có thể được trả lời bằng cách sử dụng tìm kiếm nhị phân và Merge Sort Tree, nhưng độ phức tạp thời gian cho một truy vấn đơn lẻ sẽ là $O(\log^3 n)$. Chúng ta sẽ hoàn thành nhiệm vụ tương tự bằng cách sử dụng Segment Tree persistent trong $O(\log n)$.
Đầu tiên chúng ta sẽ thảo luận về một giải pháp cho một vấn đề đơn giản hơn: Chúng ta sẽ chỉ xem xét các mảng trong đó các phần tử bị giới hạn bởi $0 \le a[i] \lt n$. Và chúng ta chỉ muốn tìm phần tử nhỏ thứ $k$ trong một tiền tố nào đó của mảng $a$. Sẽ rất dễ dàng để mở rộng các ý tưởng đã phát triển sau này cho các mảng không bị hạn chế và các truy vấn đoạn không bị hạn chế. Lưu ý rằng chúng ta sẽ sử dụng chỉ mục dựa trên 1 cho $a$.
Chúng ta sẽ sử dụng một Segment Tree đếm tất cả các số xuất hiện, tức là trong Segment Tree chúng ta sẽ lưu trữ biểu đồ tần suất (histogram) của mảng. Vì vậy, các nút lá sẽ lưu trữ tần suất các giá trị $0$, $1$, $\dots$, $n-1$ sẽ xuất hiện trong mảng, và các nút khác lưu trữ có bao nhiêu số trong một phạm vi nào đó nằm trong mảng. Nói cách khác, chúng ta tạo một Segment Tree thông thường với các truy vấn tổng trên biểu đồ tần suất của mảng. Nhưng thay vì tạo tất cả $n$ Segment Trees cho mọi tiền tố có thể, chúng ta sẽ tạo một cái persistent, sẽ chứa cùng thông tin. Chúng ta sẽ bắt đầu với một Segment Tree rỗng (tất cả các số đếm sẽ là $0$) được trỏ bởi $root_0$, và thêm các phần tử $a[1]$, $a[2]$, $\dots$, $a[n]$ lần lượt. Đối với mỗi thay đổi, chúng ta sẽ nhận được một nút gốc mới, hãy gọi $root_i$ là gốc của Segment Tree sau khi chèn $i$ phần tử đầu tiên của mảng $a$. Segment Tree có gốc tại $root_i$ sẽ chứa biểu đồ tần suất của tiền tố $a[1 \dots i]$. Sử dụng Segment Tree này, chúng ta có thể tìm thấy trong thời gian $O(\log n)$ vị trí của phần tử thứ $k$ bằng cách sử dụng cùng kỹ thuật đã thảo luận trong Đếm số lượng số 0, tìm số 0 thứ $k$.
Bây giờ đến phiên bản không hạn chế của vấn đề.
Đầu tiên đối với hạn chế về các truy vấn: Thay vì chỉ thực hiện các truy vấn này trên một tiền tố của $a$, chúng ta muốn sử dụng bất kỳ đoạn tùy ý nào $a[l \dots r]$. Ở đây chúng ta cần một Segment Tree đại diện cho biểu đồ tần suất của các phần tử trong đoạn $a[l \dots r]$. Dễ thấy rằng một Segment Tree như vậy chỉ là sự khác biệt giữa Segment Tree có gốc tại $root_{r}$ và Segment Tree có gốc tại $root_{l-1}$, tức là mọi nút trong Segment Tree $[l \dots r]$ có thể được tính bằng nút của cây $root_{r}$ trừ đi nút của cây $root_{l-1}$.
Trong việc cài đặt hàm $\text{find_kth}$, điều này có thể được xử lý bằng cách truyền hai con trỏ nút và tính toán số đếm/tổng của đoạn hiện tại dưới dạng hiệu của hai số đếm/tổng của các nút.
Dưới đây là các hàm $\text{build}$, $\text{update}$ và $\text{find_kth}$ đã sửa đổi
Vertex* build(int tl, int tr) {
if (tl == tr)
return new Vertex(0);
int tm = (tl + tr) / 2;
return new Vertex(build(tl, tm), build(tm+1, tr));
}
Vertex* update(Vertex* v, int tl, int tr, int pos) {
if (tl == tr)
return new Vertex(v->sum+1);
int tm = (tl + tr) / 2;
if (pos <= tm)
return new Vertex(update(v->l, tl, tm, pos), v->r);
else
return new Vertex(v->l, update(v->r, tm+1, tr, pos));
}
int find_kth(Vertex* vl, Vertex *vr, int tl, int tr, int k) {
if (tl == tr)
return tl;
int tm = (tl + tr) / 2, left_count = vr->l->sum - vl->l->sum;
if (left_count >= k)
return find_kth(vl->l, vr->l, tl, tm, k);
return find_kth(vl->r, vr->r, tm+1, tr, k-left_count);
}
Như đã viết ở trên, chúng ta cần lưu trữ gốc của Segment Tree ban đầu, và cả tất cả các gốc sau mỗi lần cập nhật.
Dưới đây là mã để xây dựng một Segment Tree persistent trên một vector a với các phần tử trong phạm vi [0, MAX_VALUE].
int tl = 0, tr = MAX_VALUE + 1;
std::vector<Vertex*> roots;
roots.push_back(build(tl, tr));
for (int i = 0; i < a.size(); i++) {
roots.push_back(update(roots.back(), tl, tr, a[i]));
}
// find the 5th smallest number from the subarray [a[2], a[3], ..., a[19]]
int result = find_kth(roots[2], roots[20], tl, tr, 5);
Bây giờ đến các hạn chế về các phần tử mảng: Chúng ta thực sự có thể chuyển đổi bất kỳ mảng nào thành một mảng như vậy bằng cách nén chỉ mục. Phần tử nhỏ nhất trong mảng sẽ được gán giá trị 0, nhỏ thứ hai là giá trị 1, v.v. Thật dễ dàng để tạo các bảng tra cứu (ví dụ: sử dụng $\text{map}$), chuyển đổi một giá trị thành chỉ số của nó và ngược lại trong thời gian $O(\log n)$.
Segment tree động (Dynamic segment tree)¶
(Được gọi như vậy vì hình dạng của nó là động và các nút thường được phân bổ động. Còn được gọi là implicit segment tree (segment tree ngầm) hoặc sparse segment tree (segment tree thưa).)
Trước đây, chúng ta đã xem xét các trường hợp khi chúng ta có khả năng xây dựng segment tree ban đầu. Nhưng phải làm gì nếu kích thước ban đầu được lấp đầy bằng một số phần tử mặc định, nhưng kích thước của nó không cho phép bạn xây dựng hoàn toàn cho đến nó trước?
Chúng ta có thể giải quyết vấn đề này bằng cách tạo một segment tree một cách lười biếng (tăng dần). Ban đầu, chúng ta sẽ chỉ tạo gốc, và chúng ta sẽ chỉ tạo các nút khác khi chúng ta cần chúng. Trong trường hợp này, chúng ta sẽ sử dụng cài đặt trên con trỏ (trước khi đi đến con của nút, hãy kiểm tra xem chúng đã được tạo chưa, và nếu chưa, hãy tạo chúng). Mỗi truy vấn vẫn chỉ có độ phức tạp $O(\log n)$, đủ nhỏ cho hầu hết các trường hợp sử dụng (ví dụ: $\log_2 10^9 \approx 30$).
Trong cài đặt này, chúng ta có hai truy vấn, thêm một giá trị vào một vị trí (ban đầu tất cả các giá trị là $0$), và tính tổng của tất cả các giá trị trong một đoạn.
Vertex(0, n) sẽ là nút gốc của cây ngầm.
struct Vertex {
int left, right;
int sum = 0;
Vertex *left_child = nullptr, *right_child = nullptr;
Vertex(int lb, int rb) {
left = lb;
right = rb;
}
void extend() {
if (!left_child && left + 1 < right) {
int t = (left + right) / 2;
left_child = new Vertex(left, t);
right_child = new Vertex(t, right);
}
}
void add(int k, int x) {
extend();
sum += x;
if (left_child) {
if (k < left_child->right)
left_child->add(k, x);
else
right_child->add(k, x);
}
}
int get_sum(int lq, int rq) {
if (lq <= left && right <= rq)
return sum;
if (max(left, lq) >= min(right, rq))
return 0;
extend();
return left_child->get_sum(lq, rq) + right_child->get_sum(lq, rq);
}
};
Rõ ràng ý tưởng này có thể được mở rộng theo nhiều cách khác nhau. Ví dụ: bằng cách thêm hỗ trợ cho cập nhật đoạn thông qua lazy propagation.
Bài tập (Practice Problems)¶
- SPOJ - KQUERY [Persistent segment tree / Merge sort tree]
- Codeforces - Xenia and Bit Operations
- UVA 11402 - Ahoy, Pirates!
- SPOJ - GSS3
- Codeforces - Distinct Characters Queries
- Codeforces - Knight Tournament [For beginners]
- Codeforces - Ant colony
- Codeforces - Drazil and Park
- Codeforces - Circular RMQ
- Codeforces - Lucky Array
- Codeforces - The Child and Sequence
- Codeforces - DZY Loves Fibonacci Numbers [Lazy propagation]
- Codeforces - Alphabet Permutations
- Codeforces - Eyes Closed
- Codeforces - Kefa and Watch
- Codeforces - A Simple Task
- Codeforces - SUM and REPLACE
- Codeforces - XOR on Segment [Lazy propagation]
- Codeforces - Please, another Queries on Array? [Lazy propagation]
- COCI - Deda [Last element smaller or equal to x / Binary search]
- Codeforces - The Untended Antiquity [2D]
- CSES - Hotel Queries
- CSES - Polynomial Queries
- CSES - Range Updates and Sums