Skip to content

Tìm cặp điểm gần nhất (Finding the nearest pair of points)

Phát biểu bài toán (Problem statement)

Cho $n$ điểm trên mặt phẳng. Mỗi điểm $p_i$ được xác định bởi tọa độ $(x_i,y_i)$ của nó. Yêu cầu tìm trong số chúng hai điểm sao cho khoảng cách giữa chúng là nhỏ nhất:

$$ \min_{\scriptstyle i, j=0 \ldots n-1,\atop \scriptstyle i \neq j } \rho (p_i, p_j). $$

Chúng ta lấy khoảng cách Euclide thông thường:

$$ \rho (p_i,p_j) = \sqrt{(x_i-x_j)^2 + (y_i-y_j)^2} .$$

Thuật toán tầm thường - lặp qua tất cả các cặp và tính toán khoảng cách cho mỗi cặp — hoạt động trong $O(n^2)$.

Thuật toán chạy trong thời gian $O(n \log n)$ được mô tả dưới đây. Thuật toán này được đề xuất bởi Shamos và Hoey vào năm 1975. (Nguồn: Chương 5 Ghi chú của Algorithm Design bởi Kleinberg & Tardos, xem thêm tại đây) Preparata và Shamos cũng đã chỉ ra rằng thuật toán này là tối ưu trong mô hình cây quyết định (decision tree model).

Thuật toán (Algorithm)

Chúng ta xây dựng một thuật toán theo lược đồ chung của các thuật toán chia để trị (divide-and-conquer): thuật toán được thiết kế như một hàm đệ quy, mà chúng ta truyền vào một tập hợp các điểm; hàm đệ quy này chia tập hợp này làm đôi, gọi chính nó một cách đệ quy trên mỗi nửa, và sau đó thực hiện một số thao tác để kết hợp các câu trả lời. Thao tác kết hợp bao gồm việc phát hiện các trường hợp khi một điểm của giải pháp tối ưu rơi vào một nửa, và điểm kia vào nửa kia (trong trường hợp này, các lệnh gọi đệ quy từ mỗi nửa không thể phát hiện cặp này một cách riêng biệt). Khó khăn chính, như mọi khi trong trường hợp các thuật toán chia để trị, nằm ở việc cài đặt hiệu quả giai đoạn hợp nhất (merging stage). Nếu một tập hợp $n$ điểm được truyền cho hàm đệ quy, thì giai đoạn hợp nhất sẽ hoạt động không quá $O(n)$, thì tiệm cận của toàn bộ thuật toán $T(n)$ sẽ được tìm thấy từ phương trình:

$$T(n) = 2T(n/2) + O(n).$$

Nghiệm của phương trình này, như đã biết, là $T(n) = O(n \log n).$

Vì vậy, chúng ta tiến hành xây dựng thuật toán. Để đi đến việc cài đặt hiệu quả giai đoạn hợp nhất trong tương lai, chúng ta sẽ chia tập hợp các điểm thành hai tập hợp con, theo tọa độ $x$ của chúng: Trên thực tế, chúng ta vẽ một đường thẳng đứng chia tập hợp các điểm thành hai tập hợp con có kích thước xấp xỉ nhau. Thuận tiện để thực hiện phân vùng như vậy như sau: Chúng ta sắp xếp các điểm theo cách tiêu chuẩn như các cặp số, tức là:

$$p_i < p_j \Longleftrightarrow (x_i < x_j) \lor \Big(\left(x_i = x_j\right) \wedge \left(y_i < y_j \right) \Big) $$

Sau đó lấy điểm giữa sau khi sắp xếp $p_m (m = \lfloor n/2 \rfloor)$, và tất cả các điểm trước nó và chính $p_m$ được gán cho nửa đầu tiên, và tất cả các điểm sau nó - cho nửa thứ hai:

$$A_1 = \{p_i \ | \ i = 0 \ldots m \}$$
$$A_2 = \{p_i \ | \ i = m + 1 \ldots n-1 \}.$$

Bây giờ, gọi đệ quy trên mỗi tập hợp $A_1$ và $A_2$, chúng ta sẽ tìm thấy các câu trả lời $h_1$ và $h_2$ cho mỗi nửa. Và lấy cái tốt nhất trong số chúng: $h = \min(h_1, h_2)$.

Bây giờ chúng ta cần thực hiện một giai đoạn hợp nhất, tức là chúng ta cố gắng tìm các cặp điểm như vậy, mà khoảng cách giữa chúng nhỏ hơn $h$ và một điểm nằm trong $A_1$ và điểm kia nằm trong $A_2$. Rõ ràng là chỉ cần xem xét những điểm tách biệt khỏi đường thẳng đứng một khoảng cách nhỏ hơn $h$, tức là tập hợp $B$ của các điểm được xem xét ở giai đoạn này bằng:

$$B = \{ p_i\ | \ | x_i - x_m\ | < h \}.$$

Đối với mỗi điểm trong tập hợp $B$, chúng ta cố gắng tìm các điểm gần nó hơn $h$. Ví dụ, chỉ cần xem xét những điểm có tọa độ $y$ khác biệt không quá $h$. Hơn nữa, không có ý nghĩa gì khi xem xét những điểm có tọa độ $y$ lớn hơn tọa độ $y$ của điểm hiện tại. Do đó, đối với mỗi điểm $p_i$, chúng ta định nghĩa tập hợp các điểm được xem xét $C(p_i)$ như sau:

$$C(p_i) = \{ p_j\ |\ p_j \in B,\ \ y_i - h < y_j \le y_i \}.$$

Nếu chúng ta sắp xếp các điểm của tập hợp $B$ theo tọa độ $y$, sẽ rất dễ dàng để tìm $C(p_i)$: đây là một vài điểm liên tiếp phía trước điểm $p_i$.

Vì vậy, trong ký hiệu mới, giai đoạn hợp nhất trông giống như sau: xây dựng một tập hợp $B$, sắp xếp các điểm trong đó theo tọa độ $y$, sau đó đối với mỗi điểm $p_i \in B$ xem xét tất cả các điểm $p_j \in C(p_i)$, và đối với mỗi cặp $(p_i,p_j)$ tính toán khoảng cách và so sánh với khoảng cách tốt nhất hiện tại.

Thoạt nhìn, đây vẫn là một thuật toán không tối ưu: có vẻ như kích thước của các tập hợp $C(p_i)$ sẽ có bậc $n$, và tiệm cận cần thiết sẽ không hoạt động. Tuy nhiên, đáng ngạc nhiên, có thể chứng minh rằng kích thước của mỗi tập hợp $C(p_i)$ là một lượng $O(1)$, tức là nó không vượt quá một hằng số nhỏ bất kể chính các điểm đó. Bằng chứng về thực tế này được đưa ra trong phần tiếp theo.

Cuối cùng, chúng ta chú ý đến việc sắp xếp, mà thuật toán trên chứa: đầu tiên, sắp xếp theo các cặp $(x, y)$, và sau đó thứ hai, sắp xếp các phần tử của tập hợp $B$ theo $y$. Trên thực tế, cả hai loại sắp xếp này bên trong hàm đệ quy có thể được loại bỏ (nếu không chúng ta sẽ không đạt được ước tính $O(n)$ cho giai đoạn hợp nhất, và tiệm cận chung của thuật toán sẽ là $O(n \log^2 n)$). Dễ dàng loại bỏ việc sắp xếp đầu tiên — chỉ cần thực hiện việc sắp xếp này trước khi bắt đầu đệ quy: rốt cuộc, các phần tử không thay đổi bên trong đệ quy, vì vậy không cần phải sắp xếp lại. Với việc sắp xếp thứ hai khó thực hiện hơn một chút, thực hiện nó trước đó sẽ không hoạt động. Nhưng, nhớ lại sắp xếp hợp nhất (merge sort), cũng hoạt động dựa trên nguyên tắc chia để trị, chúng ta có thể đơn giản nhúng việc sắp xếp này vào đệ quy của mình. Hãy để đệ quy, lấy một tập hợp các điểm (như chúng ta nhớ, được sắp xếp theo các cặp $(x, y)$), trả về cùng một tập hợp, nhưng được sắp xếp theo tọa độ $y$. Để làm điều này, chỉ cần hợp nhất (trong $O(n)$) hai kết quả được trả về bởi các lệnh gọi đệ quy. Điều này sẽ dẫn đến một tập hợp được sắp xếp theo tọa độ $y$.

Đánh giá tiệm cận (Evaluation of the asymptotics)

Để chỉ ra rằng thuật toán trên thực sự được thực thi trong $O(n \log n)$, chúng ta cần chứng minh thực tế sau: $|C(p_i)| = O(1)$.

Vì vậy, hãy xem xét một điểm $p_i$ nào đó; nhớ lại rằng tập hợp $C(p_i)$ là một tập hợp các điểm có tọa độ $y$ nằm trong đoạn $[y_i-h; y_i]$, và, hơn nữa, dọc theo tọa độ $x$, chính điểm $p_i$ và tất cả các điểm của tập hợp $C(p_i)$ nằm trong dải rộng $2h$. Nói cách khác, các điểm chúng ta đang xem xét $p_i$ và $C(p_i)$ nằm trong một hình chữ nhật kích thước $2h \times h$.

Nhiệm vụ của chúng ta là ước tính số lượng điểm tối đa có thể nằm trong hình chữ nhật này $2h \times h$; do đó, chúng ta ước tính kích thước tối đa của tập hợp $C(p_i)$. Đồng thời, khi đánh giá, chúng ta không được quên rằng có thể có các điểm lặp lại.

Hãy nhớ rằng $h$ thu được từ kết quả của hai lệnh gọi đệ quy — trên các tập hợp $A_1$ và $A_2$, và $A_1$ chứa các điểm bên trái đường phân chia và một phần trên đó, $A_2$ chứa các điểm còn lại của đường phân chia và các điểm bên phải nó. Đối với bất kỳ cặp điểm nào từ $A_1$, cũng như từ $A_2$, khoảng cách không thể nhỏ hơn $h$ — nếu không nó sẽ có nghĩa là hoạt động không chính xác của hàm đệ quy.

Để ước tính số lượng điểm tối đa trong hình chữ nhật $2h \times h$, chúng ta chia nó thành hai hình vuông $h \times h$, hình vuông thứ nhất bao gồm tất cả các điểm $C(p_i) \cap A_1$, và hình vuông thứ hai chứa tất cả các điểm khác, tức là $C(p_i) \cap A_2$. Từ các cân nhắc trên, suy ra rằng trong mỗi hình vuông này, khoảng cách giữa bất kỳ hai điểm nào ít nhất là $h$.

Chúng ta chỉ ra rằng có tối đa bốn điểm trong mỗi hình vuông. Ví dụ, điều này có thể được thực hiện như sau: chia hình vuông thành $4$ hình vuông con với các cạnh $h/2$. Khi đó không thể có nhiều hơn một điểm trong mỗi hình vuông con này (vì ngay cả đường chéo cũng bằng $h / \sqrt{2}$, nhỏ hơn $h$). Do đó, không thể có nhiều hơn $4$ điểm trong toàn bộ hình vuông.

Vì vậy, chúng ta đã chứng minh rằng trong một hình chữ nhật $2h \times h$ không thể có nhiều hơn $4 \cdot 2 = 8$ điểm, và do đó, kích thước của tập hợp $C(p_i)$ không thể vượt quá $7$, như yêu cầu.

Cài đặt (Implementation)

Chúng ta giới thiệu một cấu trúc dữ liệu để lưu trữ một điểm (tọa độ và một số của nó) và các toán tử so sánh cần thiết cho hai loại sắp xếp:

nearest_pair_def
struct pt {
    int x, y, id;
};

struct cmp_x {
    bool operator()(const pt & a, const pt & b) const {
        return a.x < b.x || (a.x == b.x && a.y < b.y);
    }
};

struct cmp_y {
    bool operator()(const pt & a, const pt & b) const {
        return a.y < b.y;
    }
};

int n;
vector<pt> a;

Để cài đặt thuận tiện đệ quy, chúng ta giới thiệu một hàm phụ trợ upd_ans(), sẽ tính toán khoảng cách giữa hai điểm và kiểm tra xem nó có tốt hơn câu trả lời hiện tại hay không:

nearest_pair_update
double mindist;
pair<int, int> best_pair;

void upd_ans(const pt & a, const pt & b) {
    double dist = sqrt((a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y - b.y));
    if (dist < mindist) {
        mindist = dist;
        best_pair = {a.id, b.id};
    }
}

Cuối cùng, việc cài đặt đệ quy chính nó. Giả sử rằng trước khi gọi nó, mảng $a[]$ đã được sắp xếp theo tọa độ $x$. Trong đệ quy, chúng ta chỉ truyền hai con trỏ $l, r$, cho biết rằng nó nên tìm câu trả lời cho $a[l \ldots r)$. Nếu khoảng cách giữa $r$ và $l$ quá nhỏ, đệ quy phải dừng lại, và thực hiện một thuật toán tầm thường để tìm cặp gần nhất và sau đó sắp xếp mảng con theo tọa độ $y$.

Để hợp nhất hai tập hợp điểm nhận được từ các lệnh gọi đệ quy thành một (được sắp xếp theo tọa độ $y$), chúng ta sử dụng hàm merge() tiêu chuẩn của STL, và tạo một bộ đệm phụ trợ $t[]$ (một cho tất cả các lệnh gọi đệ quy). (Sử dụng inplace_merge() là không thực tế vì nó thường không hoạt động trong thời gian tuyến tính.)

Cuối cùng, tập hợp $B$ được lưu trữ trong cùng mảng $t$.

nearest_pair_rec
vector<pt> t;

void rec(int l, int r) {
    if (r - l <= 3) {
        for (int i = l; i < r; ++i) {
            for (int j = i + 1; j < r; ++j) {
                upd_ans(a[i], a[j]);
            }
        }
        sort(a.begin() + l, a.begin() + r, cmp_y());
        return;
    }

    int m = (l + r) >> 1;
    int midx = a[m].x;
    rec(l, m);
    rec(m, r);

    merge(a.begin() + l, a.begin() + m, a.begin() + m, a.begin() + r, t.begin(), cmp_y());
    copy(t.begin(), t.begin() + r - l, a.begin() + l);

    int tsz = 0;
    for (int i = l; i < r; ++i) {
        if (abs(a[i].x - midx) < mindist) {
            for (int j = tsz - 1; j >= 0 && a[i].y - t[j].y < mindist; --j)
                upd_ans(a[i], t[j]);
            t[tsz++] = a[i];
        }
    }
}

Nhân tiện, nếu tất cả các tọa độ là số nguyên, thì tại thời điểm đệ quy bạn không thể chuyển sang các giá trị phân số, và lưu trữ trong $mindist$ bình phương của khoảng cách tối thiểu.

Trong chương trình chính, đệ quy nên được gọi như sau:

nearest_pair_main
t.resize(n);
sort(a.begin(), a.end(), cmp_x());
mindist = 1E20;
rec(0, n);

Các thuật toán ngẫu nhiên thời gian tuyến tính (Linear time randomized algorithms)

Một thuật toán ngẫu nhiên với thời gian kỳ vọng tuyến tính (A randomized algorithm with linear expected time)

Một phương pháp thay thế, ban đầu được đề xuất bởi Rabin vào năm 1976, nảy sinh từ một ý tưởng rất đơn giản để cải thiện thời gian chạy theo kinh nghiệm: Chúng ta có thể chia mặt phẳng thành một lưới các hình vuông $d \times d$, sau đó chỉ cần kiểm tra khoảng cách giữa các điểm cùng khối hoặc khối liền kề (trừ khi tất cả các hình vuông đều bị ngắt kết nối với nhau, nhưng chúng ta sẽ tránh điều này bằng thiết kế), vì bất kỳ cặp nào khác đều có khoảng cách lớn hơn hai điểm trong cùng một hình vuông.

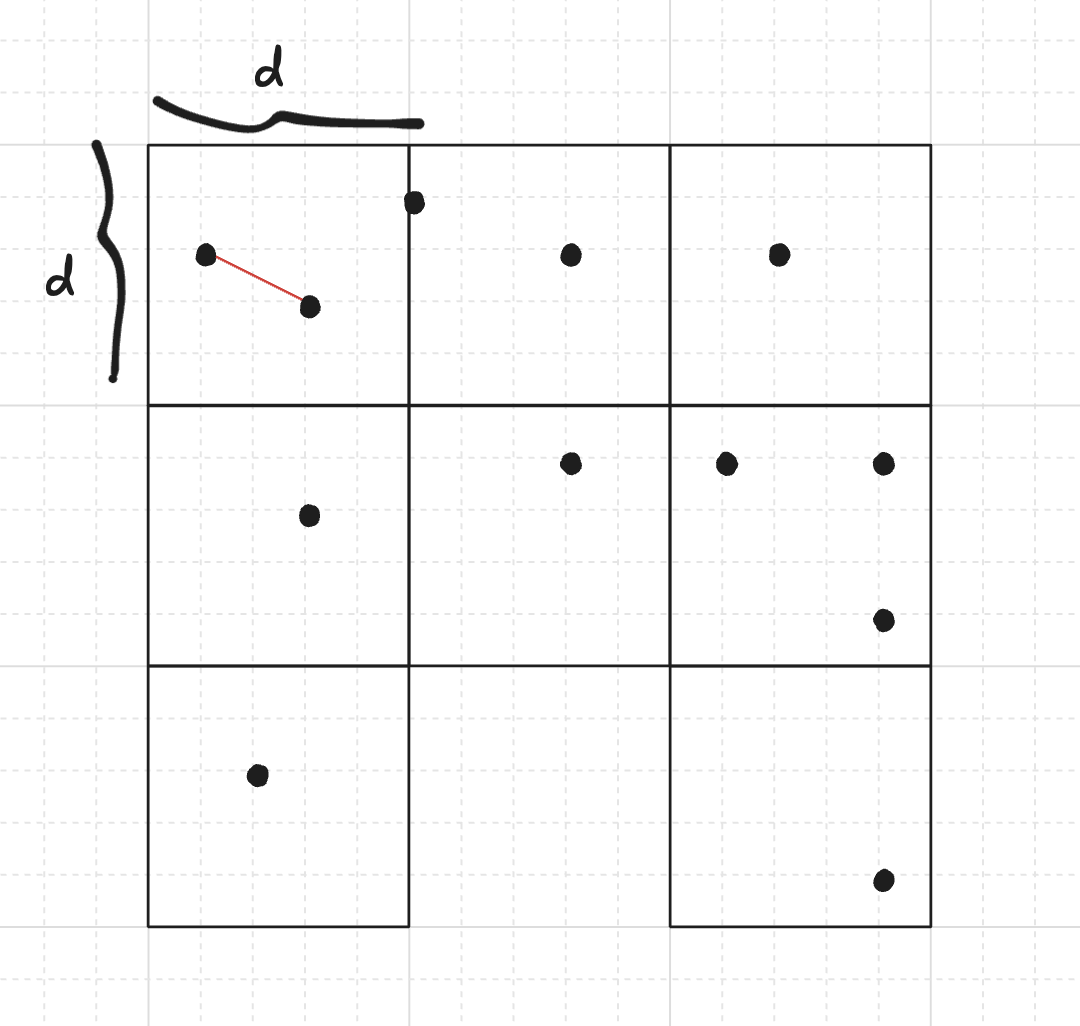
Example of the squares strategy

Chúng ta sẽ chỉ xem xét các hình vuông chứa ít nhất một điểm. Ký hiệu $n_1, n_2, \dots, n_k$ là số lượng điểm trong mỗi hình vuông trong số $k$ hình vuông còn lại. Giả sử có ít nhất hai điểm nằm trong cùng một hình vuông hoặc trong các hình vuông liền kề, và không có điểm trùng lặp, độ phức tạp thời gian là $\Theta\!\left(\sum\limits_{i=1}^k n_i^2\right)$. Chúng ta có thể tìm các điểm trùng lặp trong thời gian kỳ vọng tuyến tính bằng cách sử dụng bảng băm, và trong trường hợp khẳng định, câu trả lời là cặp này.

Minh chứng (Proof)

Đối với hình vuông thứ $i$ chứa $n_i$ điểm, số lượng cặp bên trong là $\Theta(n_i^2)$. Nếu hình vuông thứ $i$ liền kề với hình vuông thứ $j$, thì chúng ta cũng thực hiện $n_i n_j \le \max(n_i, n_j)^2 \le n_i^2 + n_j^2$ phép so sánh khoảng cách. Lưu ý rằng mỗi hình vuông có tối đa $8$ hình vuông liền kề, vì vậy chúng ta có thể giới hạn tổng của tất cả các phép so sánh bằng $\Theta(\sum_{i=1}^{k} n_i^2)$. $\quad \blacksquare$

Bây giờ chúng ta cần quyết định cách đặt $d$ sao cho nó giảm thiểu $\Theta\!\left(\sum\limits_{i=1}^k n_i^2\right)$.

Chọn d (Choosing d)

Chúng ta cần $d$ là một xấp xỉ của khoảng cách tối thiểu $d$. Richard Lipton đã đề xuất lấy mẫu $n$ khoảng cách ngẫu nhiên và chọn $d$ là khoảng cách nhỏ nhất trong số các khoảng cách này làm xấp xỉ cho $d$. Bây giờ chúng ta chứng minh rằng thời gian chạy kỳ vọng của thuật toán là tuyến tính.

Minh chứng (Proof)

Hãy tưởng tượng sự sắp xếp của các điểm trong các hình vuông với một lựa chọn cụ thể của $d$, giả sử $x$. Coi $d$ là một biến ngẫu nhiên, kết quả từ việc lấy mẫu khoảng cách của chúng ta. Hãy định nghĩa $C(x) := \sum_{i=1}^{k(x)} n_i(x)^2$ là ước tính chi phí cho một sự sắp xếp cụ thể khi chúng ta chọn $d=x$. Bây giờ, hãy định nghĩa $\lambda(x)$ sao cho $C(x) = \lambda(x) \, n$. Xác suất để một lựa chọn $x$ như vậy tồn tại sau khi lấy mẫu $n$ khoảng cách độc lập là bao nhiêu? Nếu một cặp duy nhất trong số các cặp được lấy mẫu có khoảng cách nhỏ hơn $x$, sự sắp xếp này sẽ được thay thế bằng $d$ nhỏ hơn. Bên trong một hình vuông, khoảng $1/16$ các cặp sẽ tạo ra một khoảng cách nhỏ hơn (hãy tưởng tượng bốn hình vuông con trong mỗi hình vuông; sử dụng nguyên lý chuồng bồ câu, ít nhất một hình vuông con có $n_i/4$ điểm), vì vậy chúng ta có khoảng $\sum_{i=1}^{k} {n_i/4 \choose 2} \approx \sum_{i=1}^{k} \frac{1}{16} {n_i \choose 2}$ cặp tạo ra $d$ cuối cùng nhỏ hơn. Điều này là, xấp xỉ, $\frac{1}{32} \sum_{i=1}^{k} n_i^2 = \frac{1}{32} \lambda(x) n$. Mặt khác, có khoảng $\frac{1}{2} n^2$ cặp có thể được lấy mẫu. Chúng ta có xác suất lấy mẫu một cặp có khoảng cách nhỏ hơn $x$ ít nhất là (xấp xỉ)

$$\frac{\lambda(x) \, n / 32}{n^2 / 2} = \frac{\lambda(x)/16}{n}$$

vì vậy xác suất có ít nhất một cặp như vậy được chọn trong $n$ vòng (và do đó tìm thấy $d$ nhỏ hơn) là

$$1 - \left(1 - \frac{\lambda(x)/16}{n}\right)^n \ge 1 - e^{-\lambda(x)/16}$$

(chúng ta đã sử dụng $(1 + x)^n \le e^{xn}$ cho bất kỳ số thực $x$ nào, hãy kiểm tra bất đẳng thức Bernoulli).
Lưu ý điều này tiến tới $1$ theo cấp số nhân khi $\lambda(x)$ tăng. Điều này gợi ý rằng $\lambda$ sẽ nhỏ đối với $d$ được chọn kém.

Chúng ta đã chỉ ra rằng $\Pr(d \le x) \ge 1 - e^{-\lambda(x)/16}$, hoặc tương đương, $\Pr(d \ge x) \le e^{-\lambda(x)/16}$. Chúng ta cần biết $\Pr(\lambda(d) \ge \text{something})$ để có thể ước tính giá trị kỳ vọng của nó. Chúng ta nhận thấy rằng $\lambda(d) \ge \lambda(x) \iff d \ge x$. Điều này là do việc làm cho các hình vuông nhỏ hơn chỉ làm giảm số lượng điểm trong mỗi hình vuông (chia các điểm vào các hình vuông khác), và điều này tiếp tục làm giảm tổng bình phương. Do đó,

$$\Pr(\lambda(d) \ge \lambda(x)) = \Pr(d \ge x) \le e^{-\lambda(x)/16} \implies \Pr(\lambda(d) \ge t) \le e^{-t/16} \implies \mathbb{E}[\lambda(d)] \le \int_{0}^{+\infty} e^{-t/16} \, \mathrm{d}t = 16$$

(chúng ta đã sử dụng $E[X] = \int_0^{+\infty} \Pr(X \ge x) \, \mathrm{d}x$, hãy kiểm tra Stackexchange proof).

Cuối cùng, $\mathbb{E}[C(d)] = \mathbb{E}[\lambda(d) \, n] \le 16n$, và thời gian chạy kỳ vọng là $O(n)$, với một hệ số hằng số hợp lý. $\quad \blacksquare$

Cài đặt thuật toán (Implementation of the algorithm)

Ưu điểm của thuật toán này là nó đơn giản để thực hiện, nhưng vẫn có hiệu suất tốt trong thực tế. Đầu tiên chúng ta lấy mẫu $n$ khoảng cách và đặt $d$ là giá trị tối thiểu của các khoảng cách. Sau đó chúng ta chèn các điểm vào các "khối" bằng cách sử dụng bảng băm từ tọa độ 2D đến một vector các điểm. Cuối cùng, chỉ cần tính khoảng cách giữa các cặp cùng khối và các cặp khối liền kề. Các thao tác bảng băm có chi phí thời gian kỳ vọng $O(1)$, và do đó thuật toán của chúng ta giữ chi phí thời gian kỳ vọng $O(n)$ với một hằng số tăng lên.

Kiểm tra bài nộp này lên Library Checker.

nearest_pair_randomized
#include <bits/stdc++.h>
using namespace std;


using ll = long long;
using ld = long double;


struct pt {
    ll x, y;
    pt() {}
    pt(ll x_, ll y_) : x(x_), y(y_) {}
    void read() {
        cin >> x >> y;
    }
};

bool operator==(const pt& a, const pt& b) {
    return a.x == b.x and a.y == b.y;
}


struct CustomHashPoint {
    size_t operator()(const pt& p) const {
        static const uint64_t C = chrono::steady_clock::now().time_since_epoch().count();
        return C ^ ((p.x << 32) ^ p.y);
    }
};


ll dist2(pt a, pt b) {
    ll dx = a.x - b.x;
    ll dy = a.y - b.y;
    return dx*dx + dy*dy;
}


pair<int,int> closest_pair_of_points(vector<pt> P) {
    int n = int(P.size());
    assert(n >= 2);

    // if there is a duplicated point, we have the solution
    unordered_map<pt,int,CustomHashPoint> previous;
    for (int i = 0; i < int(P.size()); ++i) {
        auto it = previous.find(P[i]);
        if (it != previous.end()) {
            return {it->second, i};
        }
        previous[P[i]] = i;
    }

    unordered_map<pt,vector<int>,CustomHashPoint> grid;
    grid.reserve(n);

    mt19937 rd(chrono::system_clock::now().time_since_epoch().count());
    uniform_int_distribution<int> dis(0, n-1);

    ll d2 = dist2(P[0], P[1]);
    pair<int,int> closest = {0, 1};

    auto candidate_closest = [&](int i, int j) -> void {
        ll ab2 = dist2(P[i], P[j]);
        if (ab2 < d2) {
            d2 = ab2;
            closest = {i, j};
        }
    };

    for (int i = 0; i < n; ++i) {
        int j = dis(rd);
        int k = dis(rd);
        while (j == k) k = dis(rd);
        candidate_closest(j, k);
    }

    ll d = ll( sqrt(ld(d2)) + 1 );

    for (int i = 0; i < n; ++i) {
        grid[{P[i].x/d, P[i].y/d}].push_back(i);
    }

    // same block
    for (const auto& it : grid) {
        int k = int(it.second.size());
        for (int i = 0; i < k; ++i) {
            for (int j = i+1; j < k; ++j) {
                candidate_closest(it.second[i], it.second[j]);
            }
        }
    }

    // adjacent blocks
    for (const auto& it : grid) {
        auto coord = it.first;
        for (int dx = 0; dx <= 1; ++dx) {
            for (int dy = -1; dy <= 1; ++dy) {
                if (dx == 0 and dy == 0) continue;
                pt neighbour = pt(
                    coord.x  + dx, 
                    coord.y + dy
                );
                for (int i : it.second) {
                    if (not grid.count(neighbour)) continue;
                    for (int j : grid.at(neighbour)) {
                        candidate_closest(i, j);
                    }
                }
            }
        }
    }

    return closest;
}

Một thuật toán thời gian kỳ vọng tuyến tính ngẫu nhiên thay thế (An alternative randomized linear expected time algorithm)

Bây giờ chúng tôi giới thiệu một thuật toán ngẫu nhiên khác ít thực tế hơn nhưng rất dễ chứng minh rằng nó chạy trong thời gian kỳ vọng tuyến tính.

  • Hoán vị $n$ điểm một cách ngẫu nhiên
  • Lấy $\delta := \operatorname{dist}(p_1, p_2)$
  • Phân chia mặt phẳng thành các hình vuông có cạnh $\delta/2$
  • Vỡi $i = 1,2,\dots,n$:
    • Lấy hình vuông tương ứng với $p_i$
    • Lặp qua $25$ hình vuông trong vòng hai bước đến hình vuông của chúng ta trong lưới các hình vuông phân chia mặt phẳng
    • Nếu một số $p_j$ trong các hình vuông đó có $\operatorname{dist}(p_j, p_i) < \delta$, thì
      • Tính toán lại phân vùng và các hình vuông với $\delta := \operatorname{dist}(p_j, p_i)$
      • Lưu trữ các điểm $p_1, \dots, p_i$ trong các hình vuông tương ứng
    • ngược lại, lưu trữ $p_i$ trong hình vuông tương ứng
  • đầu ra $\delta$

Tính đúng đắn tuân theo thực tế là tại bất kỳ thời điểm nào chúng ta đã có một cặp nào đó với khoảng cách $\delta$, vì vậy chúng ta cố gắng tìm chỉ các cặp mới với khoảng cách nhỏ hơn $\delta$. Vì mỗi hình vuông có cạnh $\delta/2$, một cặp ứng viên có thể ở tối đa một khoảng cách của $2$ hình vuông, vì vậy đối với một điểm nhất định, chúng ta kiểm tra các ứng viên trong $25$ hình vuông xung quanh. Bất kỳ điểm nào trong một hình vuông xa hơn sẽ luôn cho khoảng cách lớn hơn $\delta$.

Mặc dù thuật toán này có thể trông chậm, vì phải tính toán lại mọi thứ nhiều lần, chúng ta có thể chỉ ra rằng tổng chi phí kỳ vọng là tuyến tính.

Minh chứng (Proof)

Gọi $X_i$ là biến ngẫu nhiên bằng $1$ khi điểm $p_i$ gây ra sự thay đổi của $\delta$ và tính toán lại các cấu trúc dữ liệu, và $0$ nếu không. Dễ dàng chỉ ra rằng chi phí là $O(n + \sum_{i=1}^{n} i X_i)$, vì ở bước thứ $i$ chúng ta chỉ xem xét $i$ điểm đầu tiên. Tuy nhiên, hóa ra $\Pr(X_i = 1) \le \frac{2}{i}$. Điều này là do ở bước thứ $i$, $\delta$ là khoảng cách của cặp gần nhất trong $\{p_1,\dots,p_i\}$, và $\Pr(X_i = 1)$ là xác suất của $p_i$ thuộc về cặp gần nhất, điều này chỉ xảy ra trong $2(i-1)$ cặp trong số $i(i-1)$ cặp có thể (giả sử tất cả các khoảng cách là khác nhau), vì vậy xác suất tối đa là $\frac{2(i-1)}{i(i-1)} = \frac{2}{i}$, vì chúng ta đã xáo trộn các điểm một cách đồng đều trước đó.

Do đó, chúng ta có thể thấy rằng chi phí kỳ vọng là

$$O\!\left(n + \sum_{i=1}^{n} i \Pr(X_i = 1)\right) \le O\!\left(n + \sum_{i=1}^{n} i \frac{2}{i}\right) = O(3n) = O(n) \quad \quad \blacksquare$$

Tổng quát hóa: tìm một tam giác có chu vi tối thiểu (Generalization: finding a triangle with minimal perimeter)

Thuật toán được mô tả ở trên được tổng quát hóa một cách thú vị cho bài toán này: trong số một tập hợp các điểm đã cho, chọn ba điểm khác nhau sao cho tổng khoảng cách từng đôi giữa chúng là nhỏ nhất.

Trên thực tế, để giải quyết bài toán này, thuật toán vẫn giữ nguyên: chúng ta chia trường thành hai nửa của đường thẳng đứng, gọi giải pháp một cách đệ quy trên cả hai nửa, chọn $minper$ tối thiểu từ các chu vi được tìm thấy, xây dựng một dải có độ dày $minper / 2$, và lặp qua tất cả các tam giác có thể cải thiện câu trả lời. (Lưu ý rằng tam giác có chu vi $\le minper$ có cạnh dài nhất $\le minper / 2$.)

Bài tập (Practice problems)