Tổng Minkowski của các đa giác lồi (Minkowski sum of convex polygons)¶
Định nghĩa (Definition)¶
Xem xét hai tập hợp điểm $A$ và $B$ trên một mặt phẳng. Tổng Minkowski $A + B$ được định nghĩa là $\{a + b| a \in A, b \in B\}$. Ở đây chúng ta sẽ xem xét trường hợp khi $A$ và $B$ bao gồm các đa giác lồi $P$ và $Q$ với phần bên trong của chúng. Trong suốt bài viết này, chúng ta sẽ xác định các đa giác với các chuỗi đỉnh có thứ tự của chúng, để các ký hiệu như $|P|$ hoặc $P_i$ có ý nghĩa. Hóa ra tổng của các đa giác lồi $P$ và $Q$ là một đa giác lồi với tối đa $|P| + |Q|$ đỉnh.
Thuật toán (Algorithm)¶
Ở đây chúng ta coi các đa giác được đánh số theo vòng tròn, tức là $P_{|P|} = P_0,\ Q_{|Q|} = Q_0$ và vân vân.
Vì kích thước của tổng là tuyến tính theo kích thước của các đa giác ban đầu, chúng ta nên nhắm đến việc tìm ra một thuật toán thời gian tuyến tính. Giả sử rằng cả hai đa giác đều được sắp xếp ngược chiều kim đồng hồ. Xem xét các chuỗi cạnh $\{\overrightarrow{P_iP_{i+1}}\}$ và $\{\overrightarrow{Q_jQ_{j+1}}\}$ được sắp xếp theo góc cực. Chúng tôi tuyên bố rằng chuỗi các cạnh của $P + Q$ có thể thu được bằng cách hợp nhất hai chuỗi này bảo tồn thứ tự góc cực và thay thế các vector cùng hướng liên tiếp bằng tổng của chúng. Việc sử dụng đơn giản ý tưởng này dẫn đến một thuật toán thời gian tuyến tính, tuy nhiên, việc khôi phục các đỉnh của $P + Q$ từ chuỗi các cạnh đòi hỏi phải cộng vector lặp đi lặp lại, điều này có thể gây ra các vấn đề về độ chính xác không mong muốn nếu chúng ta đang làm việc với tọa độ dấu chấm động, vì vậy chúng tôi sẽ mô tả một sửa đổi nhỏ của ý tưởng này.
Đầu tiên, chúng ta nên sắp xếp lại các đỉnh theo cách mà đỉnh đầu tiên của mỗi đa giác có tọa độ y thấp nhất (trong trường hợp có một vài đỉnh như vậy, hãy chọn đỉnh có tọa độ x nhỏ nhất). Sau đó, các cạnh của cả hai đa giác sẽ được sắp xếp theo góc cực, vì vậy không cần phải sắp xếp chúng thủ công. Bây giờ chúng ta tạo hai con trỏ $i$ (trỏ đến một đỉnh của $P$) và $j$ (trỏ đến một đỉnh của $Q$), cả hai ban đầu được đặt thành 0. Chúng ta lặp lại các bước sau trong khi $i < |P|$ hoặc $j < |Q|$.
-
Thêm $P_i + Q_j$ vào $P + Q$.
-
So sánh góc cực của $\overrightarrow{P_iP_{i + 1}}$ và $\overrightarrow{Q_jQ_{j+1}}$.
-
Tăng con trỏ tương ứng với góc nhỏ nhất (nếu các góc bằng nhau, tăng cả hai).
Trực quan hóa (Visualization)¶
Dưới đây là một hình ảnh trực quan đẹp, có thể giúp bạn hiểu những gì đang diễn ra.
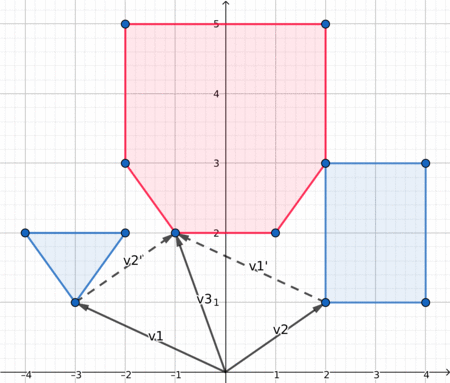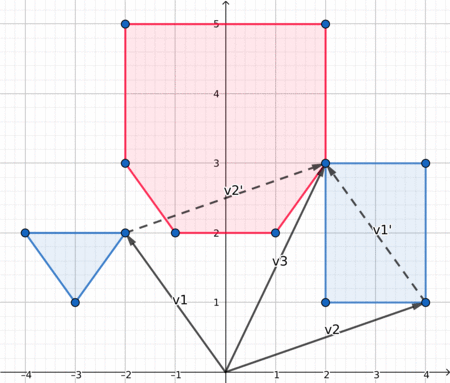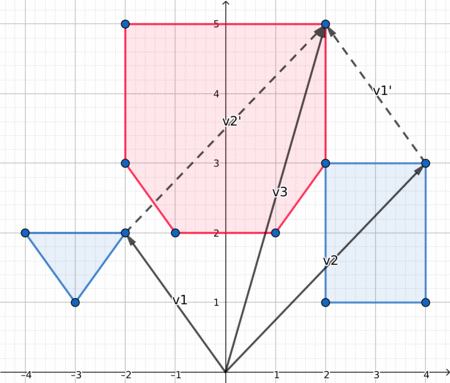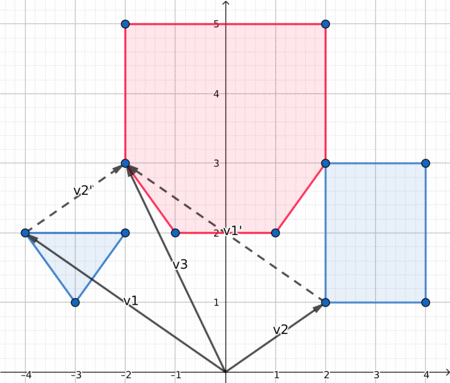
Khoảng cách giữa hai đa giác (Distance between two polygons)¶
Một trong những ứng dụng phổ biến nhất của tổng Minkowski là tính khoảng cách giữa hai đa giác lồi (hoặc đơn giản là kiểm tra xem chúng có giao nhau hay không). Khoảng cách giữa hai đa giác lồi $P$ và $Q$ được định nghĩa là $\min\limits_{a \in P, b \in Q} ||a - b||$. Người ta có thể nhận thấy rằng khoảng cách luôn đạt được giữa hai đỉnh hoặc một đỉnh và một cạnh, vì vậy chúng ta có thể dễ dàng tìm thấy khoảng cách trong $O(|P||Q|)$. Tuy nhiên, với việc sử dụng thông minh tổng Minkowski, chúng ta có thể giảm độ phức tạp xuống $O(|P| + |Q|)$.
Nếu chúng ta phản chiếu $Q$ qua điểm $(0, 0)$ thu được đa giác $-Q$, bài toán quy về việc tìm khoảng cách nhỏ nhất giữa một điểm trong $P + (-Q)$ và $(0, 0)$. Chúng ta có thể tìm thấy khoảng cách đó trong thời gian tuyến tính bằng cách sử dụng ý tưởng sau. Nếu $(0, 0)$ ở bên trong hoặc trên biên của đa giác, khoảng cách là $0$, ngược lại khoảng cách đạt được giữa $(0, 0)$ và một đỉnh hoặc cạnh nào đó của đa giác. Vì tổng Minkowski có thể được tính toán trong thời gian tuyến tính, chúng ta thu được một thuật toán thời gian tuyến tính để tìm khoảng cách giữa hai đa giác lồi.
Cài đặt (Implementation)¶
Dưới đây là việc cài đặt tổng Minkowski cho các đa giác có điểm nguyên. Lưu ý rằng trong trường hợp này, tất cả các tính toán có thể được thực hiện bằng số nguyên vì thay vì tính toán các góc cực và so sánh trực tiếp chúng, chúng ta có thể nhìn vào dấu của tích có hướng của hai vector.
struct pt{
long long x, y;
pt operator + (const pt & p) const {
return pt{x + p.x, y + p.y};
}
pt operator - (const pt & p) const {
return pt{x - p.x, y - p.y};
}
long long cross(const pt & p) const {
return x * p.y - y * p.x;
}
};
void reorder_polygon(vector<pt> & P){
size_t pos = 0;
for(size_t i = 1; i < P.size(); i++){
if(P[i].y < P[pos].y || (P[i].y == P[pos].y && P[i].x < P[pos].x))
pos = i;
}
rotate(P.begin(), P.begin() + pos, P.end());
}
vector<pt> minkowski(vector<pt> P, vector<pt> Q){
// the first vertex must be the lowest
reorder_polygon(P);
reorder_polygon(Q);
// we must ensure cyclic indexing
P.push_back(P[0]);
P.push_back(P[1]);
Q.push_back(Q[0]);
Q.push_back(Q[1]);
// main part
vector<pt> result;
size_t i = 0, j = 0;
while(i < P.size() - 2 || j < Q.size() - 2){
result.push_back(P[i] + Q[j]);
auto cross = (P[i + 1] - P[i]).cross(Q[j + 1] - Q[j]);
if(cross >= 0 && i < P.size() - 2)
++i;
if(cross <= 0 && j < Q.size() - 2)
++j;
}
return result;
}