Nguyên lý bao hàm-loại trừ (The Inclusion-Exclusion Principle)¶

Nguyên lý bao hàm-loại trừ là một cách tổ hợp quan trọng để tính kích thước của một tập hợp hoặc xác suất của các sự kiện phức tạp. Nó liên hệ kích thước của các tập hợp riêng lẻ với hợp của chúng.

Phát biểu (Statement)¶

Công thức bằng lời (The verbal formula)¶

Nguyên lý bao hàm-loại trừ có thể được diễn đạt như sau:

Để tính kích thước của một hợp của nhiều tập hợp, cần thiết phải cộng kích thước của các tập hợp này một cách riêng biệt, và sau đó trừ đi kích thước của tất cả các giao điểm từng đôi một của các tập hợp, sau đó cộng lại kích thước của các giao điểm của bộ ba các tập hợp, trừ đi kích thước của bộ bốn các tập hợp, và cứ tiếp tục như vậy, cho đến giao điểm của tất cả các tập hợp.

Công thức theo tập hợp (The formulation in terms of sets)¶

Định nghĩa trên có thể được diễn đạt bằng toán học như sau:

$$\left| \bigcup_{i=1}^n A_i \right| = \sum_{i=1}^n|A_i| - \sum_{1\leq i<j\leq n} |A_i \cap A_j| + \sum _{1\leq i<j<k\leq n}|A_i \cap A_j \cap A_k| - \cdots + (-1)^{n-1} | A_1 \cap \cdots \cap A_n |$$

Và theo một cách gọn gàng hơn:

$$\left|\bigcup_{i=1}^n A_i \right| = \sum_{\emptyset \neq J\subseteq \{1,2,\ldots ,n\}} (-1)^{|J|-1}{\Biggl |}\bigcap_{j\in J}A_{j}{\Biggr |}$$

Công thức sử dụng biểu đồ Venn (The formulation using Venn diagrams)¶

Giả sử biểu đồ hiển thị ba tập hợp $A$, $B$ và $C$:

Venn diagram

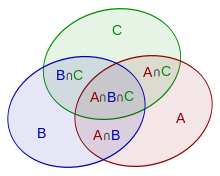
Khi đó diện tích hợp của chúng $A \cup B \cup C$ bằng tổng diện tích các phần $A$, $B$ và $C$ trừ đi các diện tích được phủ hai lần $A \cap B$, $A \cap C$, $B \cap C$, nhưng cộng thêm diện tích được bao phủ bởi ba tập hợp $A \cap B \cap C$:

$$S(A \cup B \cup C) = S(A) + S(B) + S(C) - S(A \cap B) - S(A \cap C) - S(B \cap C) + S(A \cap B \cap C)$$

Nó cũng có thể được tổng quát hóa cho một sự kết hợp của $n$ tập hợp.

Công thức theo lý thuyết xác suất (The formulation in terms of probability theory)¶

Nếu $A_i$ $(i = 1,2...n)$ là các sự kiện và ${\cal P}(A_i)$ là xác suất để một sự kiện từ $A_i$ xảy ra, thì xác suất hợp của chúng (tức là xác suất để ít nhất một trong các sự kiện xảy ra) bằng:

$$\begin{eqnarray} {\cal P} \left( \bigcup_{i=1}^n A_i \right) &=& \sum_{i=1}^n{\cal P}(A_i)\ - \sum_{1\leq i<j\leq n} {\cal P}(A_i \cap A_j)\ + \\ &+& \sum _{1\leq i<j<k\leq n}{\cal P}(A_i \cap A_j \cap A_k) - \cdots + (-1)^{n-1} {\cal P}( A_1 \cap \cdots \cap A_n ) \end{eqnarray}$$

Và theo một cách gọn gàng hơn:

$${\cal P} \left(\bigcup_{i=1}^n A_i \right) = \sum_{\emptyset \neq J\subseteq \{1,2,\ldots ,n\}} (-1)^{|J|-1}\ {\cal P}{\Biggl (}\bigcap_{j\in J}A_{j}{\Biggr )}$$

Chứng minh (Proof)¶

Để chứng minh, thuận tiện sử dụng công thức toán học theo lý thuyết tập hợp:

$$\left|\bigcup_{i=1}^n A_i \right| = \sum_{\emptyset \neq J\subseteq \{1,2,\ldots ,n\}} (-1)^{|J|-1}{\Biggl |}\bigcap_{j\in J}A_{j}{\Biggr |}$$

Chúng tôi muốn chứng minh rằng bất kỳ phần tử nào chứa trong ít nhất một trong các tập hợp $A_i$ sẽ xuất hiện trong công thức chỉ một lần (lưu ý rằng các phần tử không hiện diện trong bất kỳ tập hợp $A_i$ nào sẽ không bao giờ được xem xét ở phần bên phải của công thức).

Xem xét một phần tử $x$ xuất hiện trong $k \geq 1$ tập hợp $A_i$. Chúng tôi sẽ chỉ ra rằng nó chỉ được đếm một lần trong công thức. Lưu ý rằng:

trong các số hạng mà $|J| = 1$, mục $x$ sẽ được đếm $+\ k$ lần;
trong các số hạng mà $|J| = 2$, mục $x$ sẽ được đếm $-\ \binom{k}{2}$ lần - bởi vì nó sẽ được đếm trong các số hạng bao gồm hai trong số $k$ tập hợp chứa $x$;
trong các số hạng mà $|J| = 3$, mục $x$ sẽ được đếm $+\ \binom{k}{3}$ lần;
$\cdots$
trong các số hạng mà $|J| = k$, mục $x$ sẽ được đếm $(-1)^{k-1}\cdot \binom{k}{k}$ lần;
trong các số hạng mà $|J| \gt k$, mục $x$ sẽ được đếm không lần;

Điều này dẫn chúng ta đến tổng sau của hệ số nhị thức:

$$ T = \binom{k}{1} - \binom{k}{2} + \binom{k}{3} - \cdots + (-1)^{i-1}\cdot \binom{k}{i} + \cdots + (-1)^{k-1}\cdot \binom{k}{k}$$

Biểu thức này rất giống với khai triển nhị thức của $(1 - x)^k$:

$$ (1 - x)^k = \binom{k}{0} - \binom{k}{1} \cdot x + \binom{k}{2} \cdot x^2 - \binom{k}{3} \cdot x^3 + \cdots + (-1)^k\cdot \binom{k}{k} \cdot x^k $$

Khi $x = 1$, $(1 - x)^k$ trông rất giống $T$. Tuy nhiên, biểu thức có thêm $\binom{k}{0} = 1$, và nó được nhân với $-1$. Điều đó dẫn chúng ta đến $(1 - 1)^k = 1 - T$. Do đó $T = 1 - (1 - 1)^k = 1$, điều cần phải chứng minh. Phần tử chỉ được đếm một lần.

Tổng quát hóa để tính số lượng phần tử trong chính xác $r$ tập hợp (Generalization for calculating number of elements in exactly $r$ sets)¶

Nguyên lý bao hàm-loại trừ có thể được viết lại để tính số lượng phần tử hiện diện trong không tập hợp:

$$\left|\bigcap_{i=1}^n \overline{A_i}\right|=\sum_{m=0}^n (-1)^m \sum_{|X|=m} \left|\bigcap_{i\in X} A_{i}\right|$$

Xem xét tổng quát hóa của nó để tính số lượng phần tử hiện diện trong chính xác $r$ tập hợp:

$$\left|\bigcup_{|B|=r}\left[\bigcap_{i \in B} A_i \cap \bigcap_{j \not\in B} \overline{A_j}\right]\right|=\sum_{m=r}^n (-1)^{m-r}\dbinom{m}{r} \sum_{|X|=m} \left|\bigcap_{i \in X} A_{i}\right|$$

Để chứng minh công thức này, hãy xem xét một $B$ cụ thể nào đó. Do nguyên lý bao hàm-loại trừ cơ bản, chúng ta có thể nói về nó rằng:

$$\left|\bigcap_{i \in B} A_i \cap \bigcap_{j \not \in B} \overline{A_j}\right|=\sum_{m=r}^{n} (-1)^{m-r} \sum_{\substack{|X|=m \newline B \subset X}}\left|\bigcap_{i\in X} A_{i}\right|$$

Các tập hợp ở phía bên tráu không giao nhau đối với các $B$ khác nhau, do đó chúng ta có thể tính tổng trực tiếp. Ngoài ra, cần lưu ý rằng bất kỳ tập hợp $X$ nào cũng sẽ luôn có hệ số $(-1)^{m-r}$ nếu nó xuất hiện và nó sẽ xuất hiện cho chính xác $\dbinom{m}{r}$ tập hợp $B$.

Sử dụng khi giải các bài toán (Usage when solving problems)¶

Nguyên lý bao hàm-loại trừ rất khó hiểu nếu không nghiên cứu các ứng dụng của nó.

Trước tiên, chúng ta sẽ xem xét ba nhiệm vụ đơn giản nhất "trên giấy", minh họa các ứng dụng của nguyên lý, và sau đó xem xét các bài toán thực tế hơn khó giải quyết nếu không có nguyên lý bao hàm-loại trừ.

Các nhiệm vụ yêu cầu "tìm số cách" đáng chú ý, vì chúng đôi khi dẫn đến các giải pháp đa thức, không nhất thiết là hàm mũ.

Một nhiệm vụ đơn giản về các hoán vị (A simple task on permutations)¶

Nhiệm vụ: đếm xem có bao nhiêu hoán vị của các số từ $0$ đến $9$ tồn tại sao cho phần tử đầu tiên lớn hơn $1$ và phần tử cuối cùng nhỏ hơn $8$.

Hãy đếm số lượng hoán vị "xấu", tức là các hoán vị trong đó phần tử đầu tiên là $\leq 1$ và/hoặc phần tử cuối cùng là $\geq 8$.

Chúng ta sẽ ký hiệu $X$ là tập hợp các hoán vị trong đó phần tử đầu tiên là $\leq 1$ và $Y$ là tập hợp các hoán vị trong đó phần tử cuối cùng là $\geq 8$. Khi đó số lượng hoán vị "xấu", như trên công thức bao hàm-loại trừ, sẽ là:

$$ |X \cup Y| = |X| + |Y| - |X \cap Y| $$

Sau một tính toán tổ hợp đơn giản, chúng ta sẽ đi đến:

$$ 2 \cdot 9! + 2 \cdot 9! - 2 \cdot 2 \cdot 8! $$

Điều duy nhất còn lại là trừ số này khỏi tổng số $10!$ để có được số lượng hoán vị "tốt".

Một nhiệm vụ đơn giản về các chuỗi (0, 1, 2) (A simple task on (0, 1, 2) sequences)¶

Nhiệm vụ: đếm xem có bao nhiêu chuỗi có độ dài $n$ tồn tại chỉ bao gồm các số $0,1,2$ sao cho mỗi số xuất hiện ít nhất một lần.

Một lần nữa, chúng ta hãy chuyển sang bài toán nghịch đảo, tức là chúng ta tính số lượng chuỗi không chứa ít nhất một trong các số.

Hãy ký hiệu $A_i (i = 0,1,2)$ là tập hợp các chuỗi trong đó chữ số $i$ không xảy ra. Công thức bao hàm-loại trừ trên số lượng chuỗi "xấu" sẽ là:

$$ |A_0 \cup A_1 \cup A_2| = |A_0| + |A_1| + |A_2| - |A_0 \cap A_1| - |A_0 \cap A_2| - |A_1 \cap A_2| + |A_0 \cap A_1 \cap A_2| $$

Kích thước của mỗi $A_i$ là $2^n$, vì mỗi chuỗi chỉ có thể chứa hai trong các chữ số.
Kích thước của mỗi giao điểm từng đôi một $A_i \cap A_j$ bằng $1$, vì sẽ chỉ có một chữ số để xây dựng chuỗi.
Kích thước của giao điểm của tất cả ba tập hợp bằng $0$, vì sẽ không có chữ số nào để xây dựng chuỗi.

Vì chúng ta đã giải quyết bài toán nghịch đảo, chúng ta trừ nó khỏi tổng số $3^n$ chuỗi:

$$3^n - (3 \cdot 2^n - 3 \cdot 1 + 0)$$

Số lượng nghiệm nguyên có cận trên (Number of upper-bound integer sums)¶

Xem xét phương trình sau:

$$x_1 + x_2 + x_3 + x_4 + x_5 + x_6 = 20$$

trong đó $0 \le x_i \le 8 ~ (i = 1,2,\ldots 6)$.

Nhiệm vụ: đếm số lượng nghiệm của phương trình.

Quên hạn chế về $x_i$ trong giây lát và chỉ đếm số lượng nghiệm không âm cho phương trình này. Điều này dễ dàng được thực hiện bằng cách sử dụng Phương pháp Ngôi sao và Vách ngăn: chúng ta muốn chia một chuỗi $20$ đơn vị thành $6$ nhóm, điều này giống như sắp xếp $5$ vách ngăn và $20$ ngôi sao:

$$N_0 = \binom{25}{5}$$

Bây giờ chúng ta sẽ tính toán số lượng nghiệm "xấu" với nguyên lý bao hàm-loại trừ. Các nghiệm "xấu" sẽ là những nghiệm trong đó một hoặc nhiều $x_i$ lớn hơn hoặc bằng $9$.

Ký hiệu $A_k ~ (k = 1,2\ldots 6)$ là tập hợp các nghiệm trong đó $x_k \ge 9$, và tất cả các $x_i \ge 0 ~ (i \ne k)$ khác (chúng có thể $\ge 9$ hoặc không). Để tính kích thước của $A_k$, lưu ý rằng về cơ bản chúng ta có cùng một bài toán tổ hợp đã được giải quyết trong hai đoạn trên, nhưng bây giờ $9$ đơn vị bị loại khỏi các khe và chắc chắn thuộc về nhóm đầu tiên. Vì vậy:

$$ | A_k | = \binom{16}{5} $$

Tương tự, kích thước của giao điểm giữa hai tập hợp $A_k$ và $A_p$ (cho $k \ne p$) bằng:

$$ \left| A_k \cap A_p \right| = \binom{7}{5}$$

Kích thước của mỗi giao điểm của ba tập hợp là không, vì $20$ đơn vị sẽ không đủ cho ba hoặc nhiều biến lớn hơn hoặc bằng $9$.

Kết hợp tất cả những điều này vào công thức bao hàm-loại trừ và cho biết chúng ta đã giải quyết bài toán nghịch đảo, cuối cùng chúng ta nhận được câu trả lời:

$$\binom{25}{5} - \left(\binom{6}{1} \cdot \binom{16}{5} - \binom{6}{2} \cdot \binom{7}{5}\right) $$

Điều này dễ dàng tổng quát cho $d$ số có tổng bằng $s$ với giới hạn $0 \le x_i \le b$:

$$\sum_{i=0}^d (-1)^i \binom{d}{i} \binom{s+d-1-(b+1)i}{d-1}$$

Như trên, chúng ta coi các hệ số nhị thức có chỉ số trên âm là không.

Lưu ý bài toán này cũng có thể được giải quyết bằng quy hoạch động hoặc hàm sinh. Câu trả lời bao hàm-loại trừ được tính trong thời gian $O(d)$ (giả sử các phép toán như hệ số nhị thức là thời gian hằng số), trong khi phương pháp DP đơn giản sẽ mất thời gian $O(ds)$.

Số lượng số nguyên tố cùng nhau trong một khoảng nhất định (The number of relative primes in a given interval)¶

Nhiệm vụ: cho hai số $n$ và $r$, đếm số lượng số nguyên trong khoảng $[1;r]$ nguyên tố cùng nhau với n (ước chung lớn nhất của chúng là $1$).

Hãy giải bài toán nghịch đảo - đếm số lượng số không nguyên tố cùng nhau với $n$.

Chúng ta sẽ ký hiệu các thừa số nguyên tố của $n$ là $p_i (i = 1\cdots k)$.

Có bao nhiêu số trong khoảng $[1;r]$ chia hết cho $p_i$? Câu trả lời cho câu hỏi này là:

$$ \left\lfloor \frac{ r }{ p_i } \right\rfloor $$

Tuy nhiên, nếu chúng ta chỉ đơn giản cộng các số này, một số số sẽ được tổng hợp nhiều lần (những số chia sẻ nhiều $p_i$ làm thừa số của chúng). Do đó, cần thiết phải sử dụng nguyên lý bao hàm-loại trừ.

Chúng ta sẽ lặp qua tất cả $2^k$ tập con của $p_i$, tính tích của chúng và cộng hoặc trừ số lượng bội số của tích của chúng.

Đây là một cài đặt C++:

int solve (int n, int r) {
    vector<int> p;
    for (int i=2; i*i<=n; ++i)
        if (n % i == 0) {
            p.push_back (i);
            while (n % i == 0)
                n /= i;
        }
    if (n > 1)
        p.push_back (n);

    int sum = 0;
    for (int msk=1; msk<(1<<p.size()); ++msk) {
        int mult = 1,
            bits = 0;
        for (int i=0; i<(int)p.size(); ++i)
            if (msk & (1<<i)) {
                ++bits;
                mult *= p[i];
            }

        int cur = r / mult;
        if (bits % 2 == 1)
            sum += cur;
        else
            sum -= cur;
    }

    return r - sum;
}

Độ phức tạp tiệm cận của giải pháp là $O (\sqrt{n})$.

Số lượng số nguyên trong một khoảng nhất định là bội số của ít nhất một trong các số đã cho (The number of integers in a given interval which are multiple of at least one of the given numbers)¶

Cho $n$ số $a_i$ và số $r$. Bạn muốn đếm số lượng số nguyên trong khoảng $[1; r]$ là bội số của ít nhất một trong các $a_i$.

Thuật toán giải quyết gần như giống hệt với thuật toán cho nhiệm vụ trước — xây dựng công thức bao hàm-loại trừ trên các số $a_i$, tức là mỗi số hạng trong công thức này là số lượng các số chia hết cho một tập hợp con nhất định của các số $a_i$ (nói cách khác, chia hết cho bội chung nhỏ nhất của chúng).

Vì vậy bây giờ chúng ta sẽ lặp qua tất cả $2^n$ tập con của các số nguyên $a_i$ với $O(n \log r)$ phép toán để tìm bội chung nhỏ nhất của chúng, cộng hoặc trừ số lượng bội số của nó trong khoảng. Độ phức tạp tiệm cận là $O (2^n\cdot n\cdot \log r)$.

Số lượng chuỗi thỏa mãn một mẫu đã cho (The number of strings that satisfy a given pattern)¶

Xem xét $n$ mẫu chuỗi có cùng độ dài, chỉ bao gồm các chữ cái ($a...z$) hoặc dấu hỏi. Bạn cũng được cho một số $k$. Một chuỗi khớp với một mẫu nếu nó có cùng độ dài với mẫu, và tại mỗi vị trí, hoặc các ký tự tương ứng bằng nhau hoặc ký tự trong mẫu là một dấu hỏi. Nhiệm vụ là đếm số lượng chuỗi khớp chính xác $k$ mẫu (bài toán đầu tiên) và ít nhất $k$ mẫu (bài toán thứ hai).

Lưu ý trước tiên rằng chúng ta có thể dễ dàng đếm số lượng chuỗi thỏa mãn cùng một lúc tất cả các mẫu đã chỉ định. Để làm điều này, chỉ cần "chéo" các mẫu: lặp qua các vị trí ("khe") và nhìn vào một vị trí trên tất cả các mẫu. Nếu tất cả các mẫu đều có dấu hỏi ở vị trí này, ký tự có thể là bất kỳ chữ cái nào từ $a$ đến $z$. Ngược lại, ký tự của vị trí này được xác định duy nhất bởi các mẫu không chứa dấu hỏi.

Bây giờ hãy tìm hiểu để giải quyết phiên bản đầu tiên của bài toán: khi chuỗi phải thỏa mãn chính xác $k$ mẫu.

Để giải quyết nó, lặp lại và cố định một tập hợp con cụ thể $X$ từ tập hợp các mẫu bao gồm $k$ mẫu. Sau đó chúng ta phải đếm số lượng chuỗi thỏa mãn tập hợp mẫu này, và chỉ khớp với nó, nghĩa là, chúng không khớp với bất kỳ mẫu nào khác. Chúng ta sẽ sử dụng nguyên lý bao hàm-loại trừ theo một cách hơi khác: chúng ta tính tổng trên tất cả các tập cha $Y$ (tập hợp con từ tập hợp chuỗi ban đầu chứa $X$), và hoặc cộng vào câu trả lời hiện tại hoặc trừ nó khỏi số lượng chuỗi:

$$ ans(X) = \sum_{Y \supseteq X} (-1)^{|Y|-k} \cdot f(Y) $$

Trong đó $f(Y)$ là số lượng chuỗi khớp $Y$ (ít nhất $Y$).

(Nếu bạn gặp khó khăn trong việc tìm ra điều này, bạn có thể thử vẽ Biểu đồ Venn.)

Nếu chúng ta tính tổng trên tất cả $ans(X)$, chúng ta sẽ nhận được câu trả lời cuối cùng:

$$ ans = \sum_{X ~ : ~ |X| = k} ans(X) $$

Tuy nhiên, độ phức tạp tiệm cận của giải pháp này là $O(3^k \cdot k)$. Để cải thiện nó, hãy lưu ý rằng các tính toán $ans(X)$ khác nhau thường chia sẻ các tập hợp $Y$.

Chúng ta sẽ đảo ngược công thức bao hàm-loại trừ và tính tổng theo các tập hợp $Y$. Bây giờ trở nên rõ ràng rằng cùng một tập hợp $Y$ sẽ được tính đến trong tính toán $ans(X)$ của $\binom{|Y|}{k}$ tập hợp có cùng dấu $(-1)^{|Y| - k}$.

$$ ans = \sum_{Y ~ : ~ |Y| \ge k} (-1)^{|Y|-k} \cdot \binom{|Y|}{k} \cdot f(Y) $$

Bây giờ giải pháp của chúng ta có độ phức tạp tiệm cận $O(2^k \cdot k)$.

Bây giờ chúng ta sẽ giải quyết phiên bản thứ hai của bài toán: tìm số lượng chuỗi khớp ít nhất $k$ mẫu.

Tất nhiên, chúng ta chỉ có thể sử dụng giải pháp cho phiên bản đầu tiên của bài toán và cộng các câu trả lời cho các tập hợp có kích thước lớn hơn $k$. Tuy nhiên, bạn có thể nhận thấy rằng trong bài toán này, một tập hợp |Y| được xem xét trong công thức cho tất cả các tập hợp có kích thước $\ge k$ chứa trong $Y$. Điều đó cho biết, chúng ta có thể viết phần của biểu thức đang được nhân với $f(Y)$ là:

$$ (-1)^{|Y|-k} \cdot \binom{|Y|}{k} + (-1)^{|Y|-k-1} \cdot \binom{|Y|}{k+1} + (-1)^{|Y|-k-2} \cdot \binom{|Y|}{k+2} + \cdots + (-1)^{|Y|-|Y|} \cdot \binom{|Y|}{|Y|} $$

Nhìn vào Graham's (Graham, Knuth, Patashnik. "Concrete mathematics" [1998] ), chúng ta thấy một công thức nổi tiếng cho hệ số nhị thức:

$$ \sum_{k=0}^m (-1)^k \cdot \binom{n}{k} = (-1)^m \cdot \binom{n-1}{m} $$

Áp dụng nó ở đây, chúng ta thấy rằng toàn bộ tổng của các hệ số nhị thức được giảm thiểu:

$$ (-1)^{|Y|-k} \cdot \binom{|Y|-1}{|Y|-k} $$

Do đó, đối với nhiệm vụ này, chúng tôi cũng đã thu được một giải pháp với độ phức tạp tiệm cận $O(2^k \cdot k)$:

$$ ans = \sum_{Y ~ : ~ |Y| \ge k} (-1)^{|Y|-k} \cdot \binom{|Y|-1}{|Y|-k} \cdot f(Y) $$

Số cách đi từ một ô đến ô khác (The number of ways of going from a cell to another)¶

Có một trường $n \times m$, và $k$ ô của nó là những bức tường không thể vượt qua. Một robot ban đầu ở ô $(1,1)$ (dưới cùng bên trái). Robot chỉ có thể di chuyển sang phải hoặc lên trên, và cuối cùng nó cần phải vào ô $(n,m)$, tránh tất cả các chướng ngại vật. Bạn cần đếm số cách anh ta có thể làm điều đó.

Giả sử rằng kích thước $n$ và $m$ rất lớn (giả sử, $10^9$), và số lượng $k$ nhỏ (khoảng $100$).

Bây giờ, hãy sắp xếp các chướng ngại vật theo tọa độ $x$ của chúng, và trong trường hợp bằng nhau — tọa độ $y$.

Cũng chỉ cần học cách giải quyết một bài toán không có chướng ngại vật: tức là học cách đếm số cách để đi từ ô này sang ô khác. Trong một trục, chúng ta cần đi qua $x$ ô, và trên trục kia, $y$ ô. Từ tổ hợp đơn giản, chúng ta nhận được một công thức sử dụng hệ số nhị thức:

$$\binom{x+y}{x}$$

Bây giờ để đếm số cách để đi từ ô này sang ô khác, tránh tất cả các chướng ngại vật, bạn có thể sử dụng bao hàm-loại trừ để giải bài toán nghịch đảo: đếm số cách đi qua bảng bước vào một tập hợp con các chướng ngại vật (và trừ nó khỏi tổng số cách).

Khi lặp qua một tập hợp con các chướng ngại vật mà chúng ta sẽ bước vào, để đếm số cách làm điều này chỉ cần nhân số lượng tất cả các đường đi từ ô bắt đầu đến chướng ngại vật đầu tiên trong số các chướng ngại vật đã chọn, chướng ngại vật đầu tiên đến thứ hai, v.v., và sau đó cộng hoặc trừ số này khỏi câu trả lời, theo công thức chuẩn của bao hàm-loại trừ.

Tuy nhiên, điều này một lần nữa sẽ không phải là đa thức về độ phức tạp $O(2^k \cdot k)$.

Đây là một giải pháp đa thức:

Chúng ta sẽ sử dụng quy hoạch động. Để thuận tiện, đẩy (1,1) vào đầu và (n,m) vào cuối mảng chướng ngại vật. Hãy tính các số $d[i]$ — số cách để đi từ điểm bắt đầu ($thứ 0$) đến $thứ i$, mà không bước lên bất kỳ chướng ngại vật nào khác (ngoại trừ $i$, tất nhiên). Chúng tôi sẽ tính số này cho tất cả các ô chướng ngại vật, và cả ô kết thúc nữa.

Hãy quên đi các chướng ngại vật trong một giây và chỉ đếm số lượng đường đi từ ô $0$ đến $i$. Chúng ta cần xem xét một số đường đi "xấu", những đường đi qua các chướng ngại vật, và trừ chúng khỏi tổng số cách đi từ $0$ đến $i$.

Khi xem xét một chướng ngại vật $t$ giữa $0$ và $i$ ($0 < t < i$), mà chúng ta có thể bước lên, chúng ta thấy rằng số lượng đường đi từ $0$ đến $i$ đi qua $t$ có $t$ là chướng ngại vật đầu tiên giữa bắt đầu và $i$. Chúng ta có thể tính điều đó là: $d[t]$ nhân với số lượng đường đi tùy ý từ $t$ đến $i$. Chúng ta có thể đếm số lượng cách "xấu" cộng tổng số này cho tất cả $t$ giữa $0$ và $i$.

Chúng ta có thể tính $d[i]$ trong $O(k)$ cho $O(k)$ chướng ngại vật, vì vậy giải pháp này có độ phức tạp $O(k^2)$.

Số lượng bộ bốn nguyên tố cùng nhau (The number of coprime quadruples)¶

Bạn được cho $n$ số: $a_1, a_2, \ldots, a_n$. Bạn được yêu cầu đếm số cách chọn bốn số sao cho ước chung lớn nhất kết hợp của chúng bằng một.

Chúng ta sẽ giải bài toán nghịch đảo — tính số lượng bộ bốn "xấu", tức là các bộ bốn trong đó tất cả các số đều chia hết cho một số $d > 1$.

Chúng ta sẽ sử dụng nguyên lý bao hàm-loại trừ trong khi tính tổng trên tất cả các nhóm bốn số có thể chia hết cho một ước số $d$.

$$ans = \sum_{d \ge 2} (-1)^{deg(d)-1} \cdot f(d)$$

trong đó $deg(d)$ là số lượng số nguyên tố trong phân tích thừa số của số $d$ và $f(d)$ số lượng bộ bốn chia hết cho $d$.

Để tính hàm $f(d)$, bạn chỉ cần đếm số lượng bội số của $d$ (như đã đề cập trong một nhiệm vụ trước) và sử dụng hệ số nhị thức để đếm số cách chọn bốn trong số chúng.

Do đó, sử dụng công thức bao hàm-loại trừ, chúng ta cộng số lượng các nhóm bốn chia hết cho một số nguyên tố, sau đó trừ đi số lượng bộ bốn chia hết cho tích của hai số nguyên tố, cộng các bộ bốn chia hết cho ba số nguyên tố, v.v.

Số lượng bộ ba hài hòa (The number of harmonic triplets)¶

Bạn được cho một số $n \le 10^6$. Bạn được yêu cầu đếm số lượng bộ ba $2 \le a < b < c \le n$ thỏa mãn một trong các điều kiện sau:

hoặc ${\rm gcd}(a,b) = {\rm gcd}(a,c) = {\rm gcd}(b,c) = 1$,
hoặc ${\rm gcd}(a,b) > 1, {\rm gcd}(a,c) > 1, {\rm gcd}(b,c) > 1$.

Đầu tiên, đi thẳng vào bài toán nghịch đảo — tức là đếm số lượng bộ ba không hài hòa.

Thứ hai, lưu ý rằng bất kỳ bộ ba không hài hòa nà được tạo thành từ một cặp số nguyên tố cùng nhau và một số thứ ba không nguyên tố cùng nhau với ít nhất một trong cặp đó.

Do đó, số lượng bộ ba không hài hòa chứa $i$ bằng số lượng số nguyên từ $2$ đến $n$ nguyên tố cùng nhau với $i$ nhân với số lượng số nguyên không nguyên tố cùng nhau với $i$.

Hoặc $gcd(a,b) = 1 \wedge gcd(a,c) > 1 \wedge gcd(b,c) > 1$

Hoặc $gcd(a,b) = 1 \wedge gcd(a,c) = 1 \wedge gcd(b,c) > 1$

Trong cả hai trường hợp này, nó sẽ được đếm hai lần. Trường hợp đầu tiên sẽ được đếm khi $i = a$ và khi $i = b$. Trường hợp thứ hai sẽ được đếm khi $i = b$ và khi $i = c$. Do đó, để tính số lượng bộ ba không hài hòa, chúng ta tổng hợp tính toán này thông qua tất cả $i$ từ $2$ đến $n$ và chia nó cho $2$.

Bây giờ tất cả những gì chúng ta còn lại để giải quyết là học cách đếm số lượng số nguyên tố cùng nhau với $i$ trong khoảng $[2;n]$. Mặc dù bài toán này đã được đề cập, giải pháp trên không phù hợp ở đây — nó sẽ yêu cầu phân tích thừa số của từng số nguyên từ $2$ đến $n$, và sau đó lặp qua tất cả các tập con của các số nguyên tố này.

Một giải pháp nhanh hơn là có thể với sửa đổi như vậy của sàng Eratosthenes:

Đầu tiên, chúng ta tìm tất cả các số trong khoảng $[2;n]$ sao cho phân tích thừa số đơn giản của nó không bao gồm một thừa số nguyên tố hai lần. Chúng ta cũng sẽ cần biết, đối với các số này, nó bao gồm bao nhiêu thừa số.
- Để làm điều này, chúng ta sẽ duy trì một mảng $deg[i]$ để lưu trữ số lượng số nguyên tố trong phân tích thừa số của $i$, và một mảng $good[i]$, để đánh dấu hoặc nếu $i$ chứa mỗi thừa số tối đa một lần ($good[i] = 1$) hoặc không ($good[i] = 0$). Khi lặp từ $2$ đến $n$, nếu chúng ta đạt đến một số có $deg$ bằng $0$, thì nó là một số nguyên tố và $deg$ của nó là $1$.
- Trong quá trình sàng Eratosthenes, chúng ta sẽ lặp $i$ từ $2$ đến $n$. Khi xử lý một số nguyên tố, chúng ta đi qua tất cả các bội số của nó và tăng $deg[]$ của chúng. Nếu một trong những bội số này là bội số của bình phương của $i$, thì chúng ta có thể đặt $good$ là false.
Thứ hai, chúng ta cần tính câu trả lời cho tất cả $i$ từ $2$ đến $n$, tức là, mảng $cnt[]$ — số lượng số nguyên không nguyên tố cùng nhau với $i$.
- Để làm điều này, hãy nhớ cách công thức bao hàm-loại trừ hoạt động — thực ra ở đây chúng ta thực hiện cùng một khái niệm, nhưng với logic đảo ngược: chúng ta lặp qua một thành phần (tích của các số nguyên tố từ phân tích thừa số) và cộng hoặc trừ số hạng của nó trên công thức bao hàm-loại trừ của mỗi bội số của nó.
- Vì vậy, giả sử chúng ta đang xử lý một số $i$ sao cho $good[i] = true$, tức là, nó tham gia vào công thức bao hàm-loại trừ. Lặp qua tất cả các số là bội số của $i$, và hoặc cộng hoặc trừ $\lfloor N/i \rfloor$ từ $cnt[]$ của chúng (dấu phụ thuộc vào $deg[i]$: nếu $deg[i]$ là lẻ, thì chúng ta phải cộng, nếu không thì trừ).

Dưới đây là một cài đặt C++:

int n;
bool good[MAXN];
int deg[MAXN], cnt[MAXN];

long long solve() {
    memset (good, 1, sizeof good);
    memset (deg, 0, sizeof deg);
    memset (cnt, 0, sizeof cnt);

    long long ans_bad = 0;
    for (int i=2; i<=n; ++i) {
        if (good[i]) {
            if (deg[i] == 0)  deg[i] = 1;
            for (int j=1; i*j<=n; ++j) {
                if (j > 1 && deg[i] == 1)
                    if (j % i == 0)
                        good[i*j] = false;
                    else
                        ++deg[i*j];
                cnt[i*j] += (n / i) * (deg[i]%2==1 ? +1 : -1);
            }
        }
        ans_bad += (cnt[i] - 1) * 1ll * (n-1 - cnt[i]);
    }

    return (n-1) * 1ll * (n-2) * (n-3) / 6 - ans_bad / 2;
}

Độ phức tạp tiệm cận của giải pháp của chúng ta là $O(n \log n)$, vì đối với hầu hết mọi số lên đến $n$, chúng ta thực hiện $n/i$ lần lặp trên vòng lặp lồng nhau.

Số lượng hoán vị không có điểm bất động (derangements) (The number of permutations without fixed points (derangements))¶

Chứng minh rằng số lượng hoán vị có độ dài $n$ không có điểm bất động (tức là không có số $i$ nào ở vị trí $i$ - còn được gọi là derangement) bằng số sau:

$$n! - \binom{n}{1} \cdot (n-1)! + \binom{n}{2} \cdot (n-2)! - \binom{n}{3} \cdot (n-3)! + \cdots \pm \binom{n}{n} \cdot (n-n)! $$

và xấp xỉ bằng:

$$ \frac{ n! }{ e } $$

(nếu bạn làm tròn biểu thức này đến số nguyên gần nhất — bạn nhận được chính xác số lượng hoán vị không có điểm bất động)

Ký hiệu $A_k$ là tập hợp các hoán vị có độ dài $n$ với một điểm bất động tại vị trí $k$ ($1 \le k \le n$) (tức là phần tử $k$ ở vị trí $k$).

Bây giờ chúng ta sử dụng công thức bao hàm-loại trừ để đếm số lượng hoán vị với ít nhất một điểm bất động. Đối với điều này, chúng ta cần học cách đếm kích thước của giao điểm của các tập hợp $A_i$, như sau:

$$\begin{eqnarray} \left| A_p \right| &=& (n-1)!\ , \\ \left| A_p \cap A_q \right| &=& (n-2)!\ , \\ \left| A_p \cap A_q \cap A_r \right| &=& (n-3)!\ , \\ \cdots , \end{eqnarray}$$

bởi vì nếu chúng ta biết rằng số lượng điểm bất động bằng $x$, thì chúng ta biết vị trí của $x$ phần tử của hoán vị, và tất cả $(n-x)$ phần tử khác có thể được đặt ở bất cứ đâu.

Thay thế điều này vào công thức bao hàm-loại trừ, và cho rằng số cách chọn một tập hợp con có kích thước $x$ từ tập hợp $n$ phần tử bằng $\binom{n}{x}$, chúng ta thu được công thức cho số lượng hoán vị với ít nhất một điểm bất động:

$$\binom{n}{1} \cdot (n-1)! - \binom{n}{2} \cdot (n-2)! + \binom{n}{3} \cdot (n-3)! - \cdots \pm \binom{n}{n} \cdot (n-n)! $$

Khi đó số lượng hoán vị không có điểm bất động bằng:

$$n! - \binom{n}{1} \cdot (n-1)! + \binom{n}{2} \cdot (n-2)! - \binom{n}{3} \cdot (n-3)! + \cdots \pm \binom{n}{n} \cdot (n-n)! $$

Đơn giản hóa biểu thức này, chúng ta thu được biểu thức chính xác và xấp xỉ cho số lượng hoán vị không có điểm bất động:

$$ n! \left( 1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \cdots \pm \frac{1}{n!} \right ) \approx \frac{n!}{e} $$

(bởi vì tổng trong ngoặc là $n+1$ số hạng đầu tiên của khai triển chuỗi Taylor $e^{-1}$)

Điều đáng chú ý là một bài toán tương tự có thể được giải quyết theo cách này: khi bạn cần các điểm bất động không nằm trong số $m$ phần tử đầu tiên của hoán vị (và không nằm trong số tất cả, như chúng ta vừa giải quyết). Công thức thu được giống như công thức chính xác đã cho ở trên, nhưng nó sẽ đi đến tổng của $k$, thay vì $n$.

Bài tập luyện tập¶

Danh sách các nhiệm vụ có thể được giải quyết bằng cách sử dụng nguyên lý bao hàm-loại trừ: