Phân rã dọc (Vertical decomposition)¶
Tổng quan (Overview)¶
Phân rã nhanh dọc là một kỹ thuật mạnh mẽ được sử dụng trong các bài toán hình học khác nhau. Ý tưởng chung là cắt mặt phẳng thành một vài dải dọc (vertical stripes) với một số tính chất "tốt" và giải quyết bài toán cho các dải này một cách độc lập. Chúng ta sẽ minh họa ý tưởng trên một số ví dụ.
Diện tích hợp của các tam giác (Area of the union of triangles)¶
Giả sử có $n$ tam giác trên một mặt phẳng và chúng ta phải tìm diện tích hợp của chúng. Bài toán sẽ dễ dàng nếu các tam giác không cắt nhau, vì vậy hãy loại bỏ các giao điểm này bằng cách chia mặt phẳng thành các dải dọc bằng cách vẽ các đường thẳng đứng qua tất cả các đỉnh và tất cả các giao điểm của các cạnh của các tam giác khác nhau. Có thể có $O(n^2)$ đường như vậy nên chúng ta thu được $O(n^2)$ dải. Bây giờ hãy xem xét một dải dọc nào đó. Mỗi đoạn thẳng không dọc hoặc cắt nó từ trái sang phải hoặc không cắt chút nào. Hơn nữa, không có hai đoạn thẳng nào cắt nhau hoàn toàn bên trong dải. Điều này có nghĩa là phần của hợp các tam giác nằm bên trong dải này bao gồm các hình thang rời rạc với các đáy nằm trên các cạnh của dải. Tính chất này cho phép chúng ta tính diện tích bên trong mỗi dải bằng thuật toán quét đường (scanline) sau đây. Mỗi đoạn thẳng cắt dải là đoạn trên (upper) hoặc đoạn dưới (lower), tùy thuộc vào việc phần trong của tam giác tương ứng nằm trên hay nằm dưới đoạn thẳng. Chúng ta có thể hình dung mỗi đoạn trên như một dấu ngoặc mở và mỗi đoạn dưới như một dấu ngoặc đóng và phân rã dải thành các hình thang bằng cách phân rã dãy ngoặc thành các dãy ngoặc đúng nhỏ hơn. Thuật toán này yêu cầu thời gian $O(n^3\log n)$ và bộ nhớ $O(n^2)$.
Tối ưu hóa 1 (Optimization 1)¶
Trước tiên, chúng ta sẽ giảm thời gian chạy xuống $O(n^2\log n)$. Thay vì tạo các hình thang cho mỗi dải, hãy cố định một cạnh tam giác nào đó (đoạn $s = (s_0, s_1)$) và tìm tập hợp các dải nơi đoạn này là một cạnh của một hình thang nào đó. Lưu ý rằng trong trường hợp này, chúng ta chỉ phải tìm các dải nơi cân bằng của các dấu ngoặc bên dưới (hoặc bên trên, trong trường hợp đoạn dưới) $s$ là bằng không. Điều này có nghĩa là thay vì chạy quét đường dọc cho mỗi dải, chúng ta có thể chạy quét đường ngang cho tất cả các phần của các đoạn khác ảnh hưởng đến cân bằng của các dấu ngoặc đối với $s$. Để đơn giản, chúng ta sẽ chỉ ra cách thực hiện điều này cho một đoạn trên, thuật toán cho các đoạn dưới là tương tự. Xem xét một số đoạn không dọc khác $t = (t_0, t_1)$ và tìm giao điểm $[x_1, x_2]$ của các hình chiếu của $s$ và $t$ trên $Ox$. Nếu giao điểm này rỗng hoặc chỉ bao gồm một điểm, $t$ có thể bị loại bỏ vì $s$ và $t$ không cắt phần trong của cùng một dải. Ngược lại, hãy xem xét giao điểm $I$ của $s$ và $t$. Có ba trường hợp.
-
$I = \varnothing$
Trong trường hợp này $t$ hoặc nằm trên hoặc nằm dưới $s$ trên $[x_1, x_2]$. Nếu $t$ nằm trên, nó không ảnh hưởng đến việc liệu $s$ có phải là một cạnh của một hình thang nào đó hay không. Nếu $t$ nằm dưới $s$, chúng ta nên thêm $1$ hoặc $-1$ vào cân bằng của các dãy ngoặc cho tất cả các dải trong $[x_1, x_2]$, tùy thuộc vào việc $t$ là đoạn trên hay đoạn dưới.
-
$I$ bao gồm một điểm duy nhất $p$
Trường hợp này có thể được quy về trường hợp trước bằng cách chia $[x_1, x_2]$ thành $[x_1, p_x]$ và $[p_x, x_2]$.
-
$I$ là một đoạn $l$ nào đó
Trường hợp này có nghĩa là các phần của $s$ và $t$ cho $x\in[x_1, x_2]$ trùng nhau. Nếu $t$ là đoạn dưới, $s$ rõ ràng không phải là một cạnh của hình thang. Ngược lại, có thể xảy ra trường hợp cả $s$ và $t$ đều có thể được coi là một cạnh của một hình thang nào đó. Để giải quyết sự mơ hồ này, chúng ta có thể quyết định rằng chỉ đoạn có chỉ số thấp nhất mới được coi là một cạnh (ở đây chúng ta giả sử rằng các cạnh tam giác được đánh số theo một cách nào đó). Vì vậy, nếu $index(s) < index(t)$, chúng ta nên bỏ qua trường hợp này, ngược lại chúng ta nên đánh dấu rằng $s$ không bao giờ có thể là một cạnh trên $[x_1, x_2]$ (ví dụ, bằng cách thêm một sự kiện tương ứng với cân bằng $-2$).
Dưới đây là biểu diễn đồ họa của ba trường hợp.
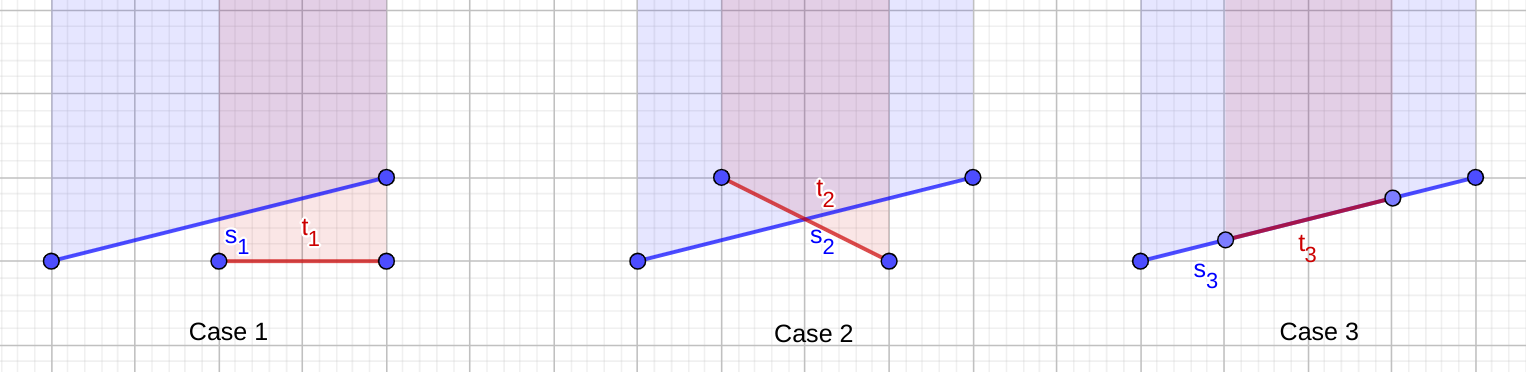
Cuối cùng, chúng ta nên nhận xét về việc xử lý tất cả các phép cộng $1$ hoặc $-1$ trên tất cả các dải trong $[x_1, x_2]$. Đối với mỗi phép cộng $w$ trên $[x_1, x_2]$ chúng ta có thể tạo các sự kiện $(x_1, w),\ (x_2, -w)$ và xử lý tất cả các sự kiện này bằng một đường quét.
Tối ưu hóa 2 (Optimization 2)¶
Lưu ý rằng nếu chúng ta áp dụng tối ưu hóa trước đó, chúng ta không còn phải tìm tất cả các dải một cách rõ ràng nữa. Điều này làm giảm mức tiêu thụ bộ nhớ xuống $O(n)$.
Giao của các đa giác lồi (Intersection of convex polygons)¶
Một cách sử dụng khác của phân rã dọc là tính toán giao của hai đa giác lồi trong thời gian tuyến tính. Giả sử mặt phẳng được chia thành các dải dọc bởi các đường thẳng đứng đi qua mỗi đỉnh của mỗi đa giác. Khi đó nếu chúng ta xem xét một trong các đa giác đầu vào và một dải nào đó, giao điểm của chúng là một hình thang, một tam giác hoặc một điểm. Do đó, chúng ta có thể chỉ cần cắt các hình này cho mỗi dải dọc và hợp nhất các giao điểm này thành một đa giác duy nhất.
Cài đặt (Implementation)¶
Dưới đây là mã tính toán diện tích hợp của một tập hợp các tam giác trong thời gian $O(n^2\log n)$ và bộ nhớ $O(n)$.
typedef double dbl;
const dbl eps = 1e-9;
inline bool eq(dbl x, dbl y){
return fabs(x - y) < eps;
}
inline bool lt(dbl x, dbl y){
return x < y - eps;
}
inline bool gt(dbl x, dbl y){
return x > y + eps;
}
inline bool le(dbl x, dbl y){
return x < y + eps;
}
inline bool ge(dbl x, dbl y){
return x > y - eps;
}
struct pt{
dbl x, y;
inline pt operator - (const pt & p)const{
return pt{x - p.x, y - p.y};
}
inline pt operator + (const pt & p)const{
return pt{x + p.x, y + p.y};
}
inline pt operator * (dbl a)const{
return pt{x * a, y * a};
}
inline dbl cross(const pt & p)const{
return x * p.y - y * p.x;
}
inline dbl dot(const pt & p)const{
return x * p.x + y * p.y;
}
inline bool operator == (const pt & p)const{
return eq(x, p.x) && eq(y, p.y);
}
};
struct Line{
pt p[2];
Line(){}
Line(pt a, pt b):p{a, b}{}
pt vec()const{
return p[1] - p[0];
}
pt& operator [](size_t i){
return p[i];
}
};
inline bool lexComp(const pt & l, const pt & r){
if(fabs(l.x - r.x) > eps){
return l.x < r.x;
}
else return l.y < r.y;
}
vector<pt> interSegSeg(Line l1, Line l2){
if(eq(l1.vec().cross(l2.vec()), 0)){
if(!eq(l1.vec().cross(l2[0] - l1[0]), 0))
return {};
if(!lexComp(l1[0], l1[1]))
swap(l1[0], l1[1]);
if(!lexComp(l2[0], l2[1]))
swap(l2[0], l2[1]);
pt l = lexComp(l1[0], l2[0]) ? l2[0] : l1[0];
pt r = lexComp(l1[1], l2[1]) ? l1[1] : l2[1];
if(l == r)
return {l};
else return lexComp(l, r) ? vector<pt>{l, r} : vector<pt>();
}
else{
dbl s = (l2[0] - l1[0]).cross(l2.vec()) / l1.vec().cross(l2.vec());
pt inter = l1[0] + l1.vec() * s;
if(ge(s, 0) && le(s, 1) && le((l2[0] - inter).dot(l2[1] - inter), 0))
return {inter};
else
return {};
}
}
inline char get_segtype(Line segment, pt other_point){
if(eq(segment[0].x, segment[1].x))
return 0;
if(!lexComp(segment[0], segment[1]))
swap(segment[0], segment[1]);
return (segment[1] - segment[0]).cross(other_point - segment[0]) > 0 ? 1 : -1;
}
dbl union_area(vector<tuple<pt, pt, pt> > triangles){
vector<Line> segments(3 * triangles.size());
vector<char> segtype(segments.size());
for(size_t i = 0; i < triangles.size(); i++){
pt a, b, c;
tie(a, b, c) = triangles[i];
segments[3 * i] = lexComp(a, b) ? Line(a, b) : Line(b, a);
segtype[3 * i] = get_segtype(segments[3 * i], c);
segments[3 * i + 1] = lexComp(b, c) ? Line(b, c) : Line(c, b);
segtype[3 * i + 1] = get_segtype(segments[3 * i + 1], a);
segments[3 * i + 2] = lexComp(c, a) ? Line(c, a) : Line(a, c);
segtype[3 * i + 2] = get_segtype(segments[3 * i + 2], b);
}
vector<dbl> k(segments.size()), b(segments.size());
for(size_t i = 0; i < segments.size(); i++){
if(segtype[i]){
k[i] = (segments[i][1].y - segments[i][0].y) / (segments[i][1].x - segments[i][0].x);
b[i] = segments[i][0].y - k[i] * segments[i][0].x;
}
}
dbl ans = 0;
for(size_t i = 0; i < segments.size(); i++){
if(!segtype[i])
continue;
dbl l = segments[i][0].x, r = segments[i][1].x;
vector<pair<dbl, int> > evts;
for(size_t j = 0; j < segments.size(); j++){
if(!segtype[j] || i == j)
continue;
dbl l1 = segments[j][0].x, r1 = segments[j][1].x;
if(ge(l1, r) || ge(l, r1))
continue;
dbl common_l = max(l, l1), common_r = min(r, r1);
auto pts = interSegSeg(segments[i], segments[j]);
if(pts.empty()){
dbl yl1 = k[j] * common_l + b[j];
dbl yl = k[i] * common_l + b[i];
if(lt(yl1, yl) == (segtype[i] == 1)){
int evt_type = -segtype[i] * segtype[j];
evts.emplace_back(common_l, evt_type);
evts.emplace_back(common_r, -evt_type);
}
}
else if(pts.size() == 1u){
dbl yl = k[i] * common_l + b[i], yl1 = k[j] * common_l + b[j];
int evt_type = -segtype[i] * segtype[j];
if(lt(yl1, yl) == (segtype[i] == 1)){
evts.emplace_back(common_l, evt_type);
evts.emplace_back(pts[0].x, -evt_type);
}
yl = k[i] * common_r + b[i], yl1 = k[j] * common_r + b[j];
if(lt(yl1, yl) == (segtype[i] == 1)){
evts.emplace_back(pts[0].x, evt_type);
evts.emplace_back(common_r, -evt_type);
}
}
else{
if(segtype[j] != segtype[i] || j > i){
evts.emplace_back(common_l, -2);
evts.emplace_back(common_r, 2);
}
}
}
evts.emplace_back(l, 0);
sort(evts.begin(), evts.end());
size_t j = 0;
int balance = 0;
while(j < evts.size()){
size_t ptr = j;
while(ptr < evts.size() && eq(evts[j].first, evts[ptr].first)){
balance += evts[ptr].second;
++ptr;
}
if(!balance && !eq(evts[j].first, r)){
dbl next_x = ptr == evts.size() ? r : evts[ptr].first;
ans -= segtype[i] * (k[i] * (next_x + evts[j].first) + 2 * b[i]) * (next_x - evts[j].first);
}
j = ptr;
}
}
return ans/2;
}