Skip to content

Thủ thuật bao lồi và Cây Li Chao (Convex hull trick and Li Chao tree)

Hãy xem xét bài toán sau. Có $n$ thành phố. Bạn muốn đi từ thành phố $1$ đến thành phố $n$ bằng ô tô. Để làm điều này, bạn phải mua một ít xăng. Người ta biết rằng một lít xăng có giá $cost_k$ tại thành phố thứ $k$. Ban đầu thùng nhiên liệu của bạn trống rỗng và bạn tiêu tốn một lít xăng cho mỗi km. Các thành phố nằm trên cùng một đường thẳng theo thứ tự tăng dần với thành phố thứ $k$ có tọa độ $x_k$. Ngoài ra bạn phải trả $toll_k$ để vào thành phố thứ $k$. Nhiệm vụ của bạn là thực hiện chuyến đi với chi phí thấp nhất có thể. Rõ ràng là giải pháp có thể được tính toán thông qua quy hoạch động:

$$dp_i = toll_i+\min\limits_{j<i}(cost_j \cdot (x_i - x_j)+dp_j)$$

Cách tiếp cận ngây thơ (naive) sẽ cho bạn độ phức tạp $O(n^2)$, có thể được cải thiện thành $O(n \log n)$ hoặc $O(n \log [C \varepsilon^{-1}])$ trong đó $C$ là giá trị lớn nhất có thể có của $|x_i|$ và $\varepsilon$ là độ chính xác mà $x_i$ được xem xét ($\varepsilon = 1$ cho các số nguyên, thường là trường hợp này). Để làm điều này, người ta nên lưu ý rằng bài toán có thể được quy về việc thêm các hàm tuyến tính $k \cdot x + b$ vào tập hợp và tìm giá trị nhỏ nhất của các hàm tại một điểm $x$ cụ thể. Có hai cách tiếp cận chính người ta có thể sử dụng ở đây.

Thủ thuật bao lồi (Convex hull trick)

Ý tưởng của cách tiếp cận này là duy trì một bao lồi dưới (lower convex hull) của các hàm tuyến tính. Thực ra sẽ thuận tiện hơn một chút nếu coi chúng không phải là các hàm tuyến tính, mà là các điểm $(k;b)$ trên mặt phẳng sao cho chúng ta sẽ phải tìm điểm có tích vô hướng nhỏ nhất với một điểm đã cho $(x;1)$, nghĩa là, đối với điểm này $kx+b$ được tối thiểu hóa, cũng chính là bài toán ban đầu. Giá trị nhỏ nhất như vậy nhất thiết sẽ nằm trên bao lồi dưới của các điểm này như có thể thấy bên dưới:

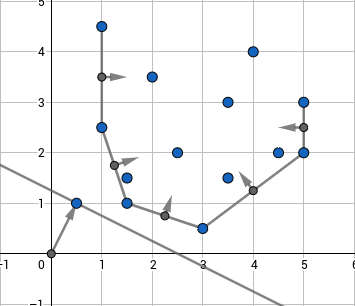
lower convex hull

Người ta phải giữ các điểm trên bao lồi và các vector pháp tuyến của các cạnh của bao. Khi bạn có một truy vấn $(x;1)$, bạn sẽ phải tìm vector pháp tuyến gần nhất với nó về mặt góc giữa chúng, sau đó hàm tuyến tính tối ưu sẽ tương ứng với một trong các điểm đầu mút của nó. Để thấy điều đó, người ta nên lưu ý rằng các điểm có tích vô hướng không đổi với $(x;1)$ nằm trên một đường thẳng trực giao với $(x;1)$, vì vậy hàm tuyến tính tối ưu sẽ là hàm mà tiếp tuyến với bao lồi cùng phương với pháp tuyến tới $(x;1)$ chạm vào bao. Điểm này là điểm sao cho các pháp tuyến của các cạnh nằm ở bên trái và bên phải của nó hướng về các phía khác nhau của $(x;1)$.

Cách tiếp cận này hữu ích khi các truy vấn thêm các hàm tuyến tính là đơn điệu theo $k$ hoặc nếu chúng ta làm việc offline, tức là chúng ta có thể thêm tất cả các hàm tuyến tính trước và trả lời các truy vấn sau đó. Vì vậy, chúng ta không thể giải quyết các vấn đề thành phố/xăng dầu bằng cách này. Điều đó đòi hỏi phải xử lý các truy vấn online. Tuy nhiên, khi nói đến việc xử lý các truy vấn online, mọi thứ sẽ trở nên khó khăn và người ta sẽ phải sử dụng một số loại cấu trúc dữ liệu tập hợp để cài đặt một bao lồi thích hợp. Tuy nhiên, cách tiếp cận online sẽ không được xem xét trong bài viết này do độ khó của nó và vì cách tiếp cận thứ hai (đó là cây Li Chao) cho phép giải quyết vấn đề đơn giản hơn nhiều. Đáng chú ý là người ta vẫn có thể sử dụng cách tiếp cận này online mà không gặp biến chứng bằng cách phân rã căn bậc hai (square-root-decomposition). Nghĩa là, xây dựng lại bao lồi từ đầu mỗi khi có $\sqrt n$ đường thẳng mới.

Để cài đặt cách tiếp cận này, người ta nên bắt đầu với một số hàm tiện ích hình học, ở đây chúng tôi khuyên bạn nên sử dụng kiểu số phức C++.

typedef int ftype;
typedef complex<ftype> point;
#define x real
#define y imag

ftype dot(point a, point b) {
    return (conj(a) * b).x();
}

ftype cross(point a, point b) {
    return (conj(a) * b).y();
}

Ở đây chúng ta sẽ giả sử rằng khi các hàm tuyến tính được thêm vào, $k$ của chúng chỉ tăng và chúng ta muốn tìm các giá trị nhỏ nhất. Chúng ta sẽ giữ các điểm trong vector hull và các vector pháp tuyến trong vector vecs. Khi chúng ta thêm một điểm mới, chúng ta phải xem xét góc được tạo ra giữa cạnh cuối cùng trong bao lồi và vector từ điểm cuối cùng trong bao lồi đến điểm mới. Góc này phải được hướng ngược chiều kim đồng hồ, nghĩa là tích vô hướng của vector pháp tuyến cuối cùng trong bao (hướng vào trong bao) và vector từ điểm cuối cùng đến điểm mới phải không âm. Chừng nào điều này không đúng, chúng ta nên xóa điểm cuối cùng trong bao lồi cùng với cạnh tương ứng.

vector<point> hull, vecs;

void add_line(ftype k, ftype b) {
    point nw = {k, b};
    while(!vecs.empty() && dot(vecs.back(), nw - hull.back()) < 0) {
        hull.pop_back();
        vecs.pop_back();
    }
    if(!hull.empty()) {
        vecs.push_back(1i * (nw - hull.back()));
    }
    hull.push_back(nw);
}
Bây giờ để lấy giá trị nhỏ nhất tại một điểm nào đó, chúng ta sẽ tìm vector pháp tuyến đầu tiên trong bao lồi hướng ngược chiều kim đồng hồ từ $(x;1)$. Điểm đầu mút bên trái của cạnh như vậy sẽ là câu trả lời. Để kiểm tra xem vector $a$ có không hướng ngược chiều kim đồng hồ của vector $b$ hay không, chúng ta nên kiểm tra xem tích có hướng (cross product) $[a,b]$ có dương hay không. 
int get(ftype x) {
    point query = {x, 1};
    auto it = lower_bound(vecs.begin(), vecs.end(), query, [](point a, point b) {
        return cross(a, b) > 0;
    });
    return dot(query, hull[it - vecs.begin()]);
}

Cây Li Chao (Li Chao tree)

Giả sử bạn được cho một tập hợp các hàm sao cho mỗi hai hàm có thể cắt nhau tối đa một lần. Hãy giữ trong mỗi đỉnh của cây phân đoạn (segment tree) một số hàm theo cách sao cho, nếu chúng ta đi từ gốc đến lá, sẽ được đảm bảo rằng một trong các hàm chúng ta gặp trên đường đi sẽ là hàm cho giá trị nhỏ nhất trong lá đó. Hãy xem cách xây dựng nó.

Giả sử chúng ta đang ở một đỉnh nào đó tương ứng với nửa đoạn $[l,r)$ và hàm $f_{old}$ được giữ ở đó và chúng ta thêm hàm $f_{new}$. Khi đó điểm giao nhau sẽ ở trong $[l;m)$ hoặc trong $[m;r)$ với $m=\left\lfloor\tfrac{l+r}{2}\right\rfloor$. Chúng ta có thể tìm ra điều đó một cách hiệu quả bằng cách so sánh các giá trị của các hàm tại các điểm $l$ và $m$. Nếu hàm chiếm ưu thế thay đổi, thì nó nằm trong $[l;m)$, ngược lại nó nằm trong $[m;r)$. Bây giờ đối với nửa đoạn không có giao điểm, chúng ta sẽ chọn hàm thấp hơn và ghi nó vào đỉnh hiện tại. Bạn có thể thấy rằng nó sẽ luôn là hàm thấp hơn tại điểm $m$. Sau đó chúng ta đệ quy đi đến nửa còn lại của đoạn với hàm là hàm trên. Như bạn có thể thấy, điều này sẽ giữ tính đúng đắn trên nửa đầu của đoạn và trong nửa còn lại tính đúng đắn sẽ được duy trì trong cuộc gọi đệ quy. Do đó chúng ta có thể thêm các hàm và kiểm tra giá trị nhỏ nhất tại điểm trong $O(\log [C\varepsilon^{-1}])$.

Đây là minh họa về những gì đang diễn ra trong đỉnh khi chúng ta thêm hàm mới:

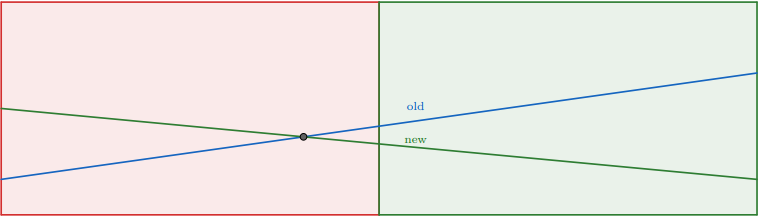
Li Chao Tree vertex

Bây giờ hãy đi đến phần cài đặt. Một lần nữa chúng ta sẽ sử dụng số phức để giữ các hàm tuyến tính.

lichaotree_line_definition
typedef long long ftype;
typedef complex<ftype> point;
#define x real
#define y imag

ftype dot(point a, point b) {
    return (conj(a) * b).x();
}

ftype f(point a,  ftype x) {
    return dot(a, {x, 1});
}
Chúng ta sẽ giữ các hàm trong mảng line và sử dụng chỉ số nhị phân của cây phân đoạn. Nếu bạn muốn sử dụng nó trên các số lớn hoặc số thực (doubles), bạn nên sử dụng cây phân đoạn động (dynamic segment tree). Cây phân đoạn nên được khởi tạo với các giá trị mặc định, ví dụ với các đường thẳng $0x + \infty$.
lichaotree_addline
const int maxn = 2e5;

point line[4 * maxn];

void add_line(point nw, int v = 1, int l = 0, int r = maxn) {
    int m = (l + r) / 2;
    bool lef = f(nw, l) < f(line[v], l);
    bool mid = f(nw, m) < f(line[v], m);
    if(mid) {
        swap(line[v], nw);
    }
    if(r - l == 1) {
        return;
    } else if(lef != mid) {
        add_line(nw, 2 * v, l, m);
    } else {
        add_line(nw, 2 * v + 1, m, r);
    }
}
Bây giờ để lấy giá trị nhỏ nhất tại một điểm $x$ nào đó, chúng ta chỉ cần chọn giá trị nhỏ nhất dọc theo đường đi đến điểm đó.
lichaotree_getminimum
ftype get(int x, int v = 1, int l = 0, int r = maxn) {
    int m = (l + r) / 2;
    if(r - l == 1) {
        return f(line[v], x);
    } else if(x < m) {
        return min(f(line[v], x), get(x, 2 * v, l, m));
    } else {
        return min(f(line[v], x), get(x, 2 * v + 1, m, r));
    }
}

Bài tập (Problems)