Tìm tiếp tuyến chung của hai đường tròn (Finding common tangents to two circles)¶
Cho hai đường tròn. Yêu cầu tìm tất cả các tiếp tuyến chung của chúng, tức là tất cả các đường thẳng tiếp xúc với cả hai đường tròn cùng một lúc.
Thuật toán được mô tả cũng sẽ hoạt động trong trường hợp một (hoặc cả hai) đường tròn suy biến thành điểm. Do đó, thuật toán này cũng có thể được sử dụng để tìm tiếp tuyến của một đường tròn đi qua một điểm đã cho.
Số lượng tiếp tuyến chung (The number of common tangents)¶
Số lượng tiếp tuyến chung của hai đường tròn có thể là 0, 1, 2, 3, 4 và vô hạn. Nhìn vào các hình ảnh cho các trường hợp khác nhau.
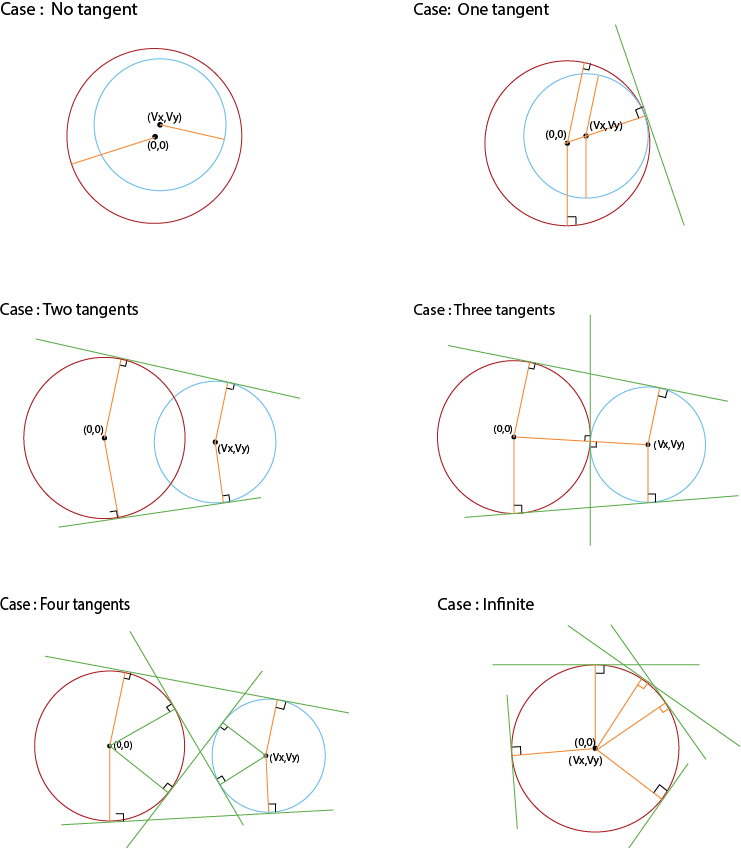
Ở đây, chúng ta sẽ không xem xét các trường hợp suy biến, tức là khi các đường tròn trùng nhau (trong trường hợp này chúng có vô số tiếp tuyến chung), hoặc một đường tròn nằm bên trong đường tròn kia (trong trường hợp này chúng không có tiếp tuyến chung, hoặc nếu các đường tròn tiếp xúc trong, có một tiếp tuyến chung).
Trong hầu hết các trường hợp, hai đường tròn có bốn tiếp tuyến chung.
Jika các đường tròn tiếp xúc, thì chúng sẽ có ba tiếp tuyến chung, nhưng điều này có thể được hiểu là một trường hợp suy biến: như thể hai tiếp tuyến trùng nhau.
Hơn nữa, thuật toán được mô tả dưới đây sẽ hoạt động trong trường hợp một hoặc cả hai đường tròn có bán kính bằng không: trong trường hợp này sẽ có tương ứng hai hoặc một tiếp tuyến chung.
Tóm lại, chúng ta sẽ luôn tìm kiếm bốn tiếp tuyến cho tất cả các trường hợp ngoại trừ trường hợp vô số tiếp tuyến (Trường hợp vô số tiếp tuyến cần được xử lý riêng và không được thảo luận ở đây). Trong các trường hợp suy biến, một số tiếp tuyến sẽ trùng nhau, nhưng tuy nhiên, các trường hợp này cũng sẽ phù hợp với bức tranh lớn.
Thuật toán (Algorithm)¶
Để đơn giản hóa thuật toán, chúng ta sẽ giả sử, không mất tính tổng quát, rằng tâm của đường tròn thứ nhất có tọa độ $(0, 0)$. (Nếu không phải như vậy, thì điều này có thể đạt được bằng cách đơn giản là dịch chuyển toàn bộ bức tranh, và sau khi tìm thấy giải pháp, bằng cách dịch chuyển các đường thẳng thu được trở lại.)
Ký hiệu $r_1$ và $r_2$ là bán kính của đường tròn thứ nhất và thứ hai, và $(v_x,v_y)$ là tọa độ của tâm của đường tròn thứ hai và điểm $v$ khác với gốc tọa độ. (Lưu ý: chúng ta không xem xét trường hợp hai đường tròn giống nhau).
Để giải quyết bài toán, chúng ta tiếp cận nó hoàn toàn bằng đại số. Chúng ta cần tìm tất cả các đường thẳng có dạng $ax + by + c = 0$ nằm ở khoảng cách $r_1$ từ gốc tọa độ, và ở khoảng cách $r_2$ từ một điểm $v$. Ngoài ra, chúng ta áp đặt điều kiện chuẩn hóa của đường thẳng: tổng bình phương của các hệ số $a$ và $b$ phải bằng một (điều này là cần thiết, nếu không cùng một đường thẳng sẽ tương ứng với vô số biểu diễn có dạng $ax + by + c = 0$). Tổng cộng chúng ta nhận được một hệ phương trình như vậy cho $a, b, c$ mong muốn:
Để loại bỏ giá trị tuyệt đối, lưu ý rằng chỉ có bốn cách để phá dấu giá trị tuyệt đối trong hệ phương trình này. Tất cả các phương pháp này có thể được xem xét bởi trường hợp tổng quát, nếu chúng ta hiểu việc phá dấu giá trị tuyệt đối như là thực tế rằng hệ số ở vế phải có thể được nhân với -1. Nói cách khác, chúng ta chuyển sang hệ phương trình này:
Đặt ký hiệu $d_1 = \pm r_1$ và $d_2 = \pm r_2$, chúng ta đi đến kết luận rằng hệ phương trình phải có bốn nghiệm:
Việc giải hệ phương trình này được quy về việc giải một phương trình bậc hai. Chúng ta sẽ bỏ qua tất cả các tính toán cồng kềnh, và ngay lập tức đưa ra câu trả lời sẵn có:
Tổng cộng chúng ta có tám nghiệm thay vì bốn. Tuy nhiên, thật dễ hiểu những quyết định thừa nảy sinh ở đâu: thực tế, trong hệ phương trình sau, chỉ cần lấy một nghiệm (ví dụ, nghiệm đầu tiên). Thực tế, ý nghĩa hình học của việc chúng ta lấy $\pm r_1$ và $\pm r_2$ là rõ ràng: chúng ta thực sự đang phân loại phía nào của mỗi đường tròn có một đường thẳng. Do đó, hai phương pháp nảy sinh khi giải hệ phương trình sau là dư thừa: chỉ cần chọn một trong hai nghiệm (tất nhiên, chỉ cần trong tất cả bốn trường hợp, bạn phải chọn cùng một họ nghiệm).
Điều cuối cùng mà chúng ta chưa xem xét là cách dịch chuyển các đường thẳng trong trường hợp đường tròn thứ nhất ban đầu không nằm ở gốc tọa độ. Tuy nhiên, mọi thứ ở đây đều đơn giản: từ tính tuyến tính của phương trình đường thẳng, suy ra rằng giá trị $a \cdot x_0 + b \cdot y_0$ (trong đó $x_0$ và $y_0$ là tọa độ của tâm ban đầu của đường tròn thứ nhất) phải được trừ khỏi hệ số $c$.
Cài đặt (Implementation)¶
Đầu tiên chúng ta mô tả tất cả các cấu trúc dữ liệu cần thiết và các định nghĩa phụ trợ khác:
struct pt {
double x, y;
pt operator- (pt p) {
pt res = { x-p.x, y-p.y };
return res;
}
};
struct circle : pt {
double r;
};
struct line {
double a, b, c;
};
const double EPS = 1E-9;
double sqr (double a) {
return a * a;
}
Sau đó, giải pháp chính nó có thể được viết theo cách này (trong đó hàm chính cho cuộc gọi là hàm thứ hai; và hàm đầu tiên là một hàm phụ trợ):
void tangents (pt c, double r1, double r2, vector<line> & ans) {
double r = r2 - r1;
double z = sqr(c.x) + sqr(c.y);
double d = z - sqr(r);
if (d < -EPS) return;
d = sqrt (abs (d));
line l;
l.a = (c.x * r + c.y * d) / z;
l.b = (c.y * r - c.x * d) / z;
l.c = r1;
ans.push_back (l);
}
vector<line> tangents (circle a, circle b) {
vector<line> ans;
for (int i=-1; i<=1; i+=2)
for (int j=-1; j<=1; j+=2)
tangents (b-a, a.r*i, b.r*j, ans);
for (size_t i=0; i<ans.size(); ++i)
ans[i].c -= ans[i].a * a.x + ans[i].b * a.y;
return ans;
}