Định vị điểm trong $O(\log n)$ (Point location in $O(\log n)$)¶
Xem xét bài toán sau: bạn được cho một phân hoạch phẳng không có bất kỳ đỉnh bậc một hay bậc không nào, và rất nhiều truy vấn.
Mỗi truy vấn là một điểm, mà chúng ta cần xác định mặt (face) của phân hoạch mà nó thuộc về.
Chúng ta sẽ trả lời từng truy vấn trong $O(\log n)$ ngoại tuyến (offline).
Vấn đề này có thể nảy sinh khi bạn cần định vị một số điểm trong biểu đồ Voronoi hoặc trong một đa giác đơn.
Thuật toán (Algorithm)¶
Đầu tiên, đối với mỗi điểm truy vấn $p\ (x_0, y_0)$ chúng ta muốn tìm một cạnh sao cho nếu điểm thuộc về bất kỳ cạnh nào, điểm đó nằm trên cạnh mà chúng ta đã tìm thấy, ngược lại cạnh này phải cắt đường thẳng $x = x_0$ tại một điểm duy nhất $(x_0, y)$ trong đó $y < y_0$ và $y$ này là lớn nhất trong số tất cả các cạnh như vậy. Hình ảnh sau đây cho thấy cả hai trường hợp.
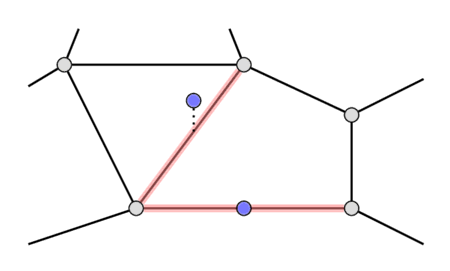
Chúng ta sẽ giải quyết bài toán này ngoại tuyến bằng thuật toán quét đường (sweep line algorithm). Hãy lặp qua các tọa độ x của các điểm truy vấn và các đầu mút của các cạnh theo thứ tự tăng dần và giữ một tập hợp các cạnh $s$. Đối với mỗi tọa độ x, chúng ta sẽ thêm một số sự kiện trước.
Các sự kiện sẽ thuộc bốn loại: add (thêm), remove (xóa), vertical (dọc), get (lấy). Đối với mỗi cạnh dọc (cả hai đầu mút đều có cùng tọa độ x), chúng ta sẽ thêm một sự kiện vertical cho tọa độ x tương ứng. Đối với mọi cạnh khác, chúng ta sẽ thêm một sự kiện add cho tọa độ x nhỏ nhất của các đầu mút và một sự kiện remove cho tọa độ x lớn nhất của các đầu mút. Cuối cùng, đối với mỗi điểm truy vấn, chúng ta sẽ thêm một sự kiện get cho tọa độ x của nó.
Đối với mỗi tọa độ x, chúng ta sẽ sắp xếp các sự kiện theo loại của chúng theo thứ tự (vertical, get, remove, add). Hình ảnh sau đây hiển thị tất cả các sự kiện theo thứ tự đã sắp xếp cho mỗi tọa độ x.
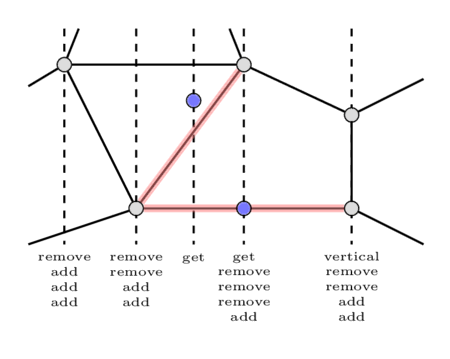
Chúng ta sẽ giữ hai tập hợp trong quá trình quét đường. Một tập hợp $t$ cho tất cả các cạnh không dọc, và một tập hợp $vert$ dành riêng cho các cạnh dọc. Chúng ta sẽ xóa tập hợp $vert$ khi bắt đầu xử lý từng tọa độ x.
Bây giờ hãy xử lý các sự kiện cho một tọa độ x cố định.
- Nếu chúng ta nhận được một sự kiện vertical, chúng ta chỉ cần chèn tọa độ y nhỏ nhất của các đầu mút của cạnh tương ứng vào $vert$.
- Nếu chúng ta nhận được một sự kiện remove hoặc add, chúng ta sẽ xóa cạnh tương ứng khỏi $t$ hoặc thêm nó vào $t$.
- Cuối cùng, đối với mỗi sự kiện get, chúng ta phải kiểm tra xem điểm có nằm trên một cạnh dọc nào đó hay không bằng cách thực hiện tìm kiếm nhị phân trong $vert$. Nếu điểm không nằm trên bất kỳ cạnh dọc nào, chúng ta phải tìm câu trả lời cho truy vấn này trong $t$. Để làm điều này, chúng ta lại thực hiện tìm kiếm nhị phân. Để xử lý một số trường hợp suy biến (ví dụ: trong trường hợp tam giác $(0,~0)$, $(0,~2)$, $(1, 1)$ khi chúng ta truy vấn điểm $(0,~0)$), chúng ta phải trả lời lại tất cả các sự kiện get sau khi chúng ta đã xử lý tất cả các sự kiện cho tọa độ x này và chọn câu trả lời tốt nhất trong hai câu trả lời.
Bây giờ hãy chọn một bộ so sánh cho tập hợp $t$.
Bộ so sánh này nên kiểm tra xem một cạnh có nằm trên cạnh khác đối với mọi tọa độ x mà cả hai đều bao phủ hay không. Giả sử rằng chúng ta có hai cạnh $(a, b)$ và $(c, d)$. Khi đó bộ so sánh là (bằng mã giả):
$val = sgn((b - a)\times(c - a)) + sgn((b - a)\times(d - a))$
if $val \neq 0$
then return $val > 0$
$val = sgn((d - c)\times(a - c)) + sgn((d - c)\times(b - c))$
return $val < 0$
Bây giờ đối với mọi truy vấn, chúng ta có cạnh tương ứng. Làm thế nào để tìm mặt (face)? Nếu chúng ta không thể tìm thấy cạnh, điều đó có nghĩa là điểm nằm ở mặt ngoài. Nếu điểm thuộc về cạnh mà chúng ta tìm thấy, mặt không phải là duy nhất. Ngược lại, có hai ứng viên - các mặt được giới hạn bởi cạnh này. Làm thế nào để kiểm tra cái nào là câu trả lời? Lưu ý rằng cạnh không phải là dọc. Khi đó câu trả lời là mặt nằm phía trên cạnh này. Hãy tìm một mặt như vậy cho mỗi cạnh không dọc. Xem xét việc duyệt ngược chiều kim đồng hồ của từng mặt. Nếu trong quá trình duyệt này, chúng ta tăng tọa độ x trong khi đi qua cạnh, thì mặt này là mặt chúng ta cần tìm cho cạnh này.
Ghi chú (Notes)¶
Thực ra, với cây bền vững (persistent trees), phương pháp này có thể được sử dụng để trả lời các truy vấn trực tuyến (online).
Cài đặt (Implementation)¶
Mã sau đây được cài đặt cho số nguyên, nhưng nó có thể dễ dàng sửa đổi để làm việc với số thực (bằng cách thay đổi các phương thức so sánh và kiểu điểm).
Việc cài đặt này giả định rằng phân hoạch được lưu trữ chính xác bên trong một DCEL và mặt ngoài được đánh số $-1$.
Đối với mỗi truy vấn, một cặp $(1, i)$ được trả về nếu điểm nằm hoàn toàn bên trong mặt số $i$, và một cặp $(0, i)$ được trả về nếu điểm nằm trên cạnh số $i$.
typedef long long ll;
bool ge(const ll& a, const ll& b) { return a >= b; }
bool le(const ll& a, const ll& b) { return a <= b; }
bool eq(const ll& a, const ll& b) { return a == b; }
bool gt(const ll& a, const ll& b) { return a > b; }
bool lt(const ll& a, const ll& b) { return a < b; }
int sgn(const ll& x) { return le(x, 0) ? eq(x, 0) ? 0 : -1 : 1; }
struct pt {
ll x, y;
pt() {}
pt(ll _x, ll _y) : x(_x), y(_y) {}
pt operator-(const pt& a) const { return pt(x - a.x, y - a.y); }
ll dot(const pt& a) const { return x * a.x + y * a.y; }
ll dot(const pt& a, const pt& b) const { return (a - *this).dot(b - *this); }
ll cross(const pt& a) const { return x * a.y - y * a.x; }
ll cross(const pt& a, const pt& b) const { return (a - *this).cross(b - *this); }
bool operator==(const pt& a) const { return a.x == x && a.y == y; }
};
struct Edge {
pt l, r;
};
bool edge_cmp(Edge* edge1, Edge* edge2)
{
const pt a = edge1->l, b = edge1->r;
const pt c = edge2->l, d = edge2->r;
int val = sgn(a.cross(b, c)) + sgn(a.cross(b, d));
if (val != 0)
return val > 0;
val = sgn(c.cross(d, a)) + sgn(c.cross(d, b));
return val < 0;
}
enum EventType { DEL = 2, ADD = 3, GET = 1, VERT = 0 };
struct Event {
EventType type;
int pos;
bool operator<(const Event& event) const { return type < event.type; }
};
vector<Edge*> sweepline(vector<Edge*> planar, vector<pt> queries)
{
using pt_type = decltype(pt::x);
// collect all x-coordinates
auto s =
set<pt_type, std::function<bool(const pt_type&, const pt_type&)>>(lt);
for (pt p : queries)
s.insert(p.x);
for (Edge* e : planar) {
s.insert(e->l.x);
s.insert(e->r.x);
}
// map all x-coordinates to ids
int cid = 0;
auto id =
map<pt_type, int, std::function<bool(const pt_type&, const pt_type&)>>(
lt);
for (auto x : s)
id[x] = cid++;
// create events
auto t = set<Edge*, decltype(*edge_cmp)>(edge_cmp);
auto vert_cmp = [](const pair<pt_type, int>& l,
const pair<pt_type, int>& r) {
if (!eq(l.first, r.first))
return lt(l.first, r.first);
return l.second < r.second;
};
auto vert = set<pair<pt_type, int>, decltype(vert_cmp)>(vert_cmp);
vector<vector<Event>> events(cid);
for (int i = 0; i < (int)queries.size(); i++) {
int x = id[queries[i].x];
events[x].push_back(Event{GET, i});
}
for (int i = 0; i < (int)planar.size(); i++) {
int lx = id[planar[i]->l.x], rx = id[planar[i]->r.x];
if (lx > rx) {
swap(lx, rx);
swap(planar[i]->l, planar[i]->r);
}
if (lx == rx) {
events[lx].push_back(Event{VERT, i});
} else {
events[lx].push_back(Event{ADD, i});
events[rx].push_back(Event{DEL, i});
}
}
// perform sweep line algorithm
vector<Edge*> ans(queries.size(), nullptr);
for (int x = 0; x < cid; x++) {
sort(events[x].begin(), events[x].end());
vert.clear();
for (Event event : events[x]) {
if (event.type == DEL) {
t.erase(planar[event.pos]);
}
if (event.type == VERT) {
vert.insert(make_pair(
min(planar[event.pos]->l.y, planar[event.pos]->r.y),
event.pos));
}
if (event.type == ADD) {
t.insert(planar[event.pos]);
}
if (event.type == GET) {
auto jt = vert.upper_bound(
make_pair(queries[event.pos].y, planar.size()));
if (jt != vert.begin()) {
--jt;
int i = jt->second;
if (ge(max(planar[i]->l.y, planar[i]->r.y),
queries[event.pos].y)) {
ans[event.pos] = planar[i];
continue;
}
}
Edge* e = new Edge;
e->l = e->r = queries[event.pos];
auto it = t.upper_bound(e);
if (it != t.begin())
ans[event.pos] = *(--it);
delete e;
}
}
for (Event event : events[x]) {
if (event.type != GET)
continue;
if (ans[event.pos] != nullptr &&
eq(ans[event.pos]->l.x, ans[event.pos]->r.x))
continue;
Edge* e = new Edge;
e->l = e->r = queries[event.pos];
auto it = t.upper_bound(e);
delete e;
if (it == t.begin())
e = nullptr;
else
e = *(--it);
if (ans[event.pos] == nullptr) {
ans[event.pos] = e;
continue;
}
if (e == nullptr)
continue;
if (e == ans[event.pos])
continue;
if (id[ans[event.pos]->r.x] == x) {
if (id[e->l.x] == x) {
if (gt(e->l.y, ans[event.pos]->r.y))
ans[event.pos] = e;
}
} else {
ans[event.pos] = e;
}
}
}
return ans;
}
struct DCEL {
struct Edge {
pt origin;
Edge* nxt = nullptr;
Edge* twin = nullptr;
int face;
};
vector<Edge*> body;
};
vector<pair<int, int>> point_location(DCEL planar, vector<pt> queries)
{
vector<pair<int, int>> ans(queries.size());
vector<Edge*> planar2;
map<intptr_t, int> pos;
map<intptr_t, int> added_on;
int n = planar.body.size();
for (int i = 0; i < n; i++) {
if (planar.body[i]->face > planar.body[i]->twin->face)
continue;
Edge* e = new Edge;
e->l = planar.body[i]->origin;
e->r = planar.body[i]->twin->origin;
added_on[(intptr_t)e] = i;
pos[(intptr_t)e] =
lt(planar.body[i]->origin.x, planar.body[i]->twin->origin.x)
? planar.body[i]->face
: planar.body[i]->twin->face;
planar2.push_back(e);
}
auto res = sweepline(planar2, queries);
for (int i = 0; i < (int)queries.size(); i++) {
if (res[i] == nullptr) {
ans[i] = make_pair(1, -1);
continue;
}
pt p = queries[i];
pt l = res[i]->l, r = res[i]->r;
if (eq(p.cross(l, r), 0) && le(p.dot(l, r), 0)) {
ans[i] = make_pair(0, added_on[(intptr_t)res[i]]);
continue;
}
ans[i] = make_pair(1, pos[(intptr_t)res[i]]);
}
for (auto e : planar2)
delete e;
return ans;
}