Skip to content

Giao của các nửa mặt phẳng (Half-plane intersection)

Trong bài viết này, chúng ta sẽ thảo luận về bài toán tính toán phần giao của một tập hợp các nửa mặt phẳng. Một phần giao như vậy có thể được biểu diễn thuận tiện dưới dạng một vùng/đa giác lồi, trong đó mọi điểm bên trong nó cũng nằm bên trong tất cả các nửa mặt phẳng, và chính đa giác này là thứ mà chúng ta đang cố gắng tìm hoặc xây dựng. Chúng tôi đưa ra một số trực giác ban đầu cho bài toán, mô tả một cách tiếp cận $O(N \log N)$ được gọi là thuật toán Sắp xếp và Tăng dần (Sort-and-Incremental algorithm) và đưa ra một số ứng dụng mẫu của kỹ thuật này.

Chúng tôi thực sự khuyên bạn đọc nên làm quen với các nguyên thủy và phép toán hình học cơ bản (điểm, vector, giao điểm của các đường thẳng). Ngoài ra, kiến thức về Bao lồi (Convex Hulls) hoặc Thủ thuật Bao lồi (Convex Hull Trick) có thể giúp hiểu rõ hơn các khái niệm trong bài viết này, nhưng chúng không phải là điều kiện tiên quyết bằng bất kỳ cách nào.

Các làm rõ và định nghĩa ban đầu (Initial clarifications and definitions)

Đối với toàn bộ bài viết, chúng tôi sẽ đưa ra một số giả định (trừ khi được chỉ định khác):

  1. Chúng ta định nghĩa $N$ là số lượng nửa mặt phẳng trong tập hợp đã cho.
  2. Chúng ta sẽ biểu diễn các đường thẳng và nửa mặt phẳng bằng một điểm và một vector (bất kỳ điểm nào nằm trên đường thẳng đã cho, và vector chỉ phương của đường thẳng). Trong trường hợp các nửa mặt phẳng, chúng ta giả định rằng mọi nửa mặt phẳng đều cho phép vùng ở phía bên trái của vector chỉ phương của nó. Ngoài ra, chúng ta định nghĩa góc của một nửa mặt phẳng là góc cực (polar angle) của vector chỉ phương của nó. Xem hình ảnh bên dưới để ví dụ.
  3. Chúng ta sẽ giả định rằng phần giao kết quả luôn bị giới hạn hoặc rỗng. Nếu chúng ta cần xử lý trường hợp không bị giới hạn, chúng ta có thể chỉ cần thêm 4 nửa mặt phẳng định nghĩa một hộp bao (bounding box) đủ lớn.
  4. Để đơn giản, chúng ta sẽ giả định rằng không có nửa mặt phẳng song song nào trong tập hợp đã cho. Về phía cuối bài viết, chúng ta sẽ thảo luận về cách giải quyết những trường hợp như vậy.

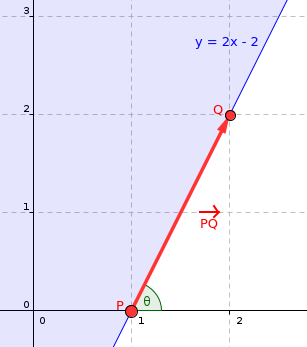
Nửa mặt phẳng $y \geq 2x - 2$ có thể được biểu diễn dưới dạng điểm $P = (1, 0)$ với vector chỉ phương $PQ = Q - P = (1, 2)$

Cách tiếp cận vết cạn - $O(N^3)$ (Brute force approach - $O(N^3)$)

Một trong những giải pháp đơn giản và rõ ràng nhất là tính toán giao điểm của các đường thẳng của tất cả các cặp nửa mặt phẳng và, đối với mỗi điểm, kiểm tra xem nó có nằm trong tất cả các nửa mặt phẳng khác hay không. Vì có $O(N^2)$ giao điểm, và đối với mỗi giao điểm, chúng ta phải kiểm tra $O(N)$ nửa mặt phẳng, tổng độ phức tạp thời gian là $O(N^3)$. Vùng thực tế của phần giao sau đó có thể được tái tạo bằng cách sử dụng, ví dụ, thuật toán Bao lồi trên tập hợp các giao điểm được bao gồm trong tất cả các nửa mặt phẳng.

Khá dễ để thấy tại sao điều này lại hoạt động: các đỉnh của đa giác lồi kết quả là tất cả các giao điểm của các đường thẳng nửa mặt phẳng, và mỗi đỉnh đó rõ ràng là một phần của tất cả các nửa mặt phẳng. Ưu điểm chính của phương pháp này là dễ hiểu, dễ nhớ và dễ viết mã ngay lập tức nếu bạn chỉ cần kiểm tra xem phần giao có rỗng hay không. Tuy nhiên, nó cực kỳ chậm và không phù hợp với hầu hết các bài toán, vì vậy chúng ta cần một cái gì đó nhanh hơn.

Cách tiếp cận tăng dần - $O(N^2)$ (Incremental approach - $O(N^2)$)

Một cách tiếp cận khá đơn giản khác là xây dựng dần dần phần giao của các nửa mặt phẳng, từng cái một. Phương pháp này về cơ bản tương đương với việc cắt một đa giác lồi bằng một đường thẳng $N$ lần, và loại bỏ các nửa mặt phẳng dư thừa ở mỗi bước. Để làm điều này, chúng ta có thể biểu diễn đa giác lồi dưới dạng danh sách các đoạn thẳng, và để cắt nó bằng một nửa mặt phẳng, chúng ta chỉ cần tìm các giao điểm của các đoạn thẳng với đường thẳng nửa mặt phẳng (sẽ chỉ có hai giao điểm nếu đường thẳng thực sự cắt đa giác), và thay thế tất cả các đoạn thẳng ở giữa bằng đoạn mới tương ứng với nửa mặt phẳng. Vì quy trình như vậy có thể được cài đặt trong thời gian tuyến tính, chúng ta có thể chỉ cần bắt đầu với một hộp bao lớn và cắt nó xuống bằng từng nửa mặt phẳng một, thu được tổng độ phức tạp thời gian là $O(N^2)$.

Phương pháp này là một bước tiến lớn đúng hướng, nhưng cảm thấy lãng phí khi phải lặp qua $O(N)$ nửa mặt phẳng ở mỗi bước. Chúng ta sẽ thấy tiếp theo rằng, bằng cách thực hiện một số quan sát thông minh, các ý tưởng đằng sau cách tiếp cận tăng dần này có thể được tái chế để tạo ra thuật toán $O(N \log N)$.

Thuật toán Sắp xếp và Tăng dần - $O(N \log N)$ (Sort-and-Incremental algorithm - $O(N \log N)$)

Nguồn đầu tiên được ghi chép đàng hoàng về thuật toán này mà chúng tôi có thể tìm thấy là luận án của Zeyuan Zhu cho Cuộc thi Chọn đội tuyển Trung Quốc có tiêu đề Thuật toán mới cho Giao của các nửa mặt phẳng và Giá trị thực tiễn của nó, từ năm 2006. Cách tiếp cận mà chúng tôi sẽ mô tả tiếp theo dựa trên cùng thuật toán này, nhưng thay vì tính toán hai giao điểm riêng biệt cho nửa dưới và nửa trên của các giao điểm, chúng tôi sẽ xây dựng tất cả cùng một lúc trong một lần chuyển qua với một deque (hàng đợi hai đầu).

Bản thân thuật toán, như tên gọi có thể tiết lộ, tận dụng thực tế là vùng kết quả từ giao của các nửa mặt phẳng là lồi, và do đó nó sẽ bao gồm một số đoạn của các nửa mặt phẳng theo thứ tự được sắp xếp theo góc của chúng. Điều này dẫn đến một quan sát quan trọng: nếu chúng ta giao dần dần các nửa mặt phẳng theo thứ tự được sắp xếp theo góc của chúng (như chúng sẽ xuất hiện trong hình dạng cuối cùng, kết quả của phần giao) và lưu trữ chúng trong một hàng đợi hai đầu, thì chúng ta sẽ chỉ cần loại bỏ các nửa mặt phẳng khỏi đầu và cuối của deque.

Để hình dung thực tế này tốt hơn, giả sử chúng ta đang thực hiện cách tiếp cận tăng dần được mô tả trước đây trên một tập hợp các nửa mặt phẳng được sắp xếp theo góc (trong trường hợp này, chúng ta sẽ giả sử chúng được sắp xếp từ $-\pi$ đến $\pi$), và giả sử rằng chúng ta sắp bắt đầu một bước thứ $k$ bất kỳ nào đó. Điều này có nghĩa là chúng ta đã xây dựng phần giao của $k-1$ nửa mặt phẳng đầu tiên. Bây giờ, bởi vì các nửa mặt phẳng được sắp xếp theo góc, bất kể nửa mặt phẳng thứ $k$ là gì, chúng ta có thể chắc chắn rằng nó sẽ tạo thành một góc lồi với nửa mặt phẳng thứ $(K-1)$. Vì lý do đó, một vài điều có thể xảy ra:

  1. Một số (có thể không có) nửa mặt phẳng ở phía sau của phần giao có thể trở nên dư thừa. Trong trường hợp này, chúng ta cần pop các nửa mặt phẳng vô dụng này khỏi phía sau của deque.
  2. Một số (có thể không có) nửa mặt phẳng ở phía trước có thể trở nên dư thừa. Tương tự như trường hợp 1, chúng ta chỉ cần pop chúng khỏi phía trước của deque.
  3. Phần giao có thể trở nên rỗng (sau khi xử lý các trường hợp 1 và/hoặc 2). Trong trường hợp này, chúng ta chỉ cần báo cáo phần giao là rỗng và kết thúc thuật toán.

Chúng ta nói một nửa mặt phẳng là "dư thừa" nếu nó không đóng góp gì vào phần giao. Nửa mặt phẳng như vậy có thể bị loại bỏ và phần giao kết quả sẽ không thay đổi chút nào.

Dưới đây là một ví dụ nhỏ với minh họa:

Gọi $H = \{ A, B, C, D, E \}$ là tập hợp các nửa mặt phẳng hiện có trong phần giao. Ngoài ra, gọi $P = \{ p, q, r, s \}$ là tập hợp các giao điểm của các nửa mặt phẳng liền kề trong H. Bây giờ, giả sử chúng ta muốn giao nó với nửa mặt phẳng $F$, như thấy trong hình minh họa bên dưới:

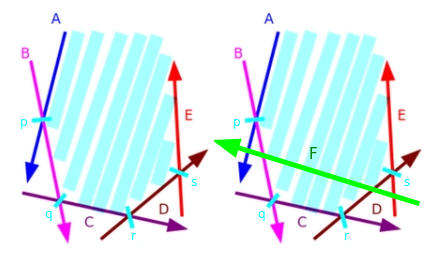
Lưu ý rằng nửa mặt phẳng $F$ làm cho $A$ và $E$ trở nên dư thừa trong phần giao. Vì vậy, chúng ta loại bỏ cả $A$ và $E$ khỏi phía trước và phía sau của phần giao, tương ứng, và thêm $F$ vào cuối. Và cuối cùng chúng ta thu được phần giao mới $H = \{ B, C, D, F\}$ với $P = \{ q, r, t, u \}$.

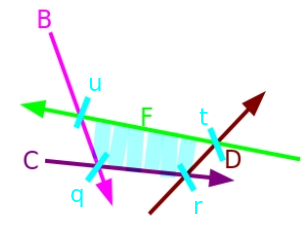
Với tất cả những điều này trong tâm trí, chúng ta có hầu hết mọi thứ chúng ta cần để thực sự cài đặt thuật toán, nhưng chúng ta vẫn cần nói về một số trường hợp đặc biệt. Ở đầu bài viết, chúng ta đã nói rằng chúng ta sẽ thêm một hộp bao để xử lý các trường hợp phần giao có thể không bị giới hạn, vì vậy trường hợp khó khăn duy nhất chúng ta thực sự cần xử lý là các nửa mặt phẳng song song. Chúng ta có thể có hai trường hợp phụ: hai nửa mặt phẳng có thể song song với cùng hướng hoặc ngược hướng. Lý do trường hợp này cần được xử lý riêng là vì chúng ta sẽ cần tính toán giao điểm của các đường thẳng nửa mặt phẳng để có thể kiểm tra xem một nửa mặt phẳng có dư thừa hay không, và hai đường thẳng song song không có giao điểm, vì vậy chúng ta cần một cách đặc biệt để đối phó với chúng.

Đối với trường hợp các nửa mặt phẳng song song có hướng ngược nhau: Lưu ý rằng, vì chúng ta đang thêm hộp bao để đối phó với trường hợp không bị giới hạn, điều này cũng giải quyết trường hợp chúng ta có hai nửa mặt phẳng song song liền kề với hướng ngược nhau sau khi sắp xếp, vì sẽ phải có ít nhất một trong các nửa mặt phẳng hộp bao ở giữa hai cái này (hãy nhớ chúng được sắp xếp theo góc).

  • Tuy nhiên, có thể xảy ra trường hợp, sau khi loại bỏ một số nửa mặt phẳng khỏi phía sau của deque, hai nửa mặt phẳng song song có hướng ngược nhau lại nằm cùng nhau. Trường hợp này chỉ xảy ra, cụ thể, khi hai nửa mặt phẳng này tạo thành một phần giao rỗng, vì nửa mặt phẳng cuối cùng này sẽ khiến mọi thứ bị loại bỏ khỏi deque. Để tránh vấn đề này, chúng ta phải kiểm tra thủ công các nửa mặt phẳng song song, và nếu chúng có hướng ngược nhau, chúng ta chỉ cần dừng ngay thuật toán và trả về phần giao rỗng.

Do đó, trường hợp duy nhất chúng ta thực sự cần xử lý là có nhiều nửa mặt phẳng với cùng một góc, và hóa ra trường hợp này khá dễ xử lý: chúng ta chỉ cần giữ nửa mặt phẳng nằm bên trái nhất và xóa phần còn lại, vì chúng sẽ hoàn toàn dư thừa dù sao đi nữa. Tóm lại, thuật toán đầy đủ sẽ trông đại khái như sau:

  1. Chúng ta bắt đầu bằng cách sắp xếp tập hợp các nửa mặt phẳng theo góc, mất thời gian $O(N \log N)$.
  2. Chúng ta sẽ lặp qua tập hợp các nửa mặt phẳng, và đối với mỗi cái, chúng ta sẽ thực hiện quy trình tăng dần, đẩy ra khỏi đầu và cuối của hàng đợi hai đầu khi cần thiết. Quá trình này sẽ mất tổng thời gian tuyến tính, vì mỗi nửa mặt phẳng chỉ có thể được thêm hoặc xóa một lần.
  3. Cuối cùng, đa giác lồi kết quả từ phần giao có thể được lấy đơn giản bằng cách tính toán các giao điểm của các nửa mặt phẳng liền kề trong deque ở cuối quy trình. Quá trình này cũng sẽ mất thời gian tuyến tính. Cũng có thể lưu trữ các điểm như vậy trong bước 2 và bỏ qua bước này hoàn toàn, nhưng chúng tôi tin rằng nó dễ dàng hơn một chút (về mặt cài đặt) để tính toán chúng ngay lập tức (on-the-fly).

Tổng cộng, chúng ta đã đạt được độ phức tạp thời gian là $O(N \log N)$. Vì việc sắp xếp rõ ràng là nút thắt cổ chai, thuật toán có thể được thực hiện để chạy trong thời gian tuyến tính trong trường hợp đặc biệt mà chúng ta được cung cấp các nửa mặt phẳng đã được sắp xếp trước theo góc của chúng (một ví dụ về trường hợp như vậy là lấy các nửa mặt phẳng xác định một đa giác lồi).

Cài đặt trực tiếp (Direct implementation)

Dưới đây là một mẫu, cài đặt trực tiếp của thuật toán, với các bình luận giải thích hầu hết các phần:

Các struct điểm/vector và nửa mặt phẳng đơn giản:

// Redefine epsilon and infinity as necessary. Be mindful of precision errors.
const long double eps = 1e-9, inf = 1e9; 

// Basic point/vector struct.
struct Point { 

    long double x, y;
    explicit Point(long double x = 0, long double y = 0) : x(x), y(y) {}

    // Addition, substraction, multiply by constant, dot product, cross product.

    friend Point operator + (const Point& p, const Point& q) {
        return Point(p.x + q.x, p.y + q.y); 
    }

    friend Point operator - (const Point& p, const Point& q) { 
        return Point(p.x - q.x, p.y - q.y); 
    }

    friend Point operator * (const Point& p, const long double& k) { 
        return Point(p.x * k, p.y * k); 
    } 

    friend long double dot(const Point& p, const Point& q) {
        return p.x * q.x + p.y * q.y;
    }

    friend long double cross(const Point& p, const Point& q) { 
        return p.x * q.y - p.y * q.x; 
    }
};

// Basic half-plane struct.
struct Halfplane { 

    // 'p' is a passing point of the line and 'pq' is the direction vector of the line.
    Point p, pq; 
    long double angle;

    Halfplane() {}
    Halfplane(const Point& a, const Point& b) : p(a), pq(b - a) {
        angle = atan2l(pq.y, pq.x);    
    }

    // Check if point 'r' is outside this half-plane. 
    // Every half-plane allows the region to the LEFT of its line.
    bool out(const Point& r) { 
        return cross(pq, r - p) < -eps; 
    }

    // Comparator for sorting. 
    bool operator < (const Halfplane& e) const { 
        return angle < e.angle;
    } 

    // Intersection point of the lines of two half-planes. It is assumed they're never parallel.
    friend Point inter(const Halfplane& s, const Halfplane& t) {
        long double alpha = cross((t.p - s.p), t.pq) / cross(s.pq, t.pq);
        return s.p + (s.pq * alpha);
    }
};

Thuật toán:

// Actual algorithm
vector<Point> hp_intersect(vector<Halfplane>& H) { 

    Point box[4] = {  // Bounding box in CCW order
        Point(inf, inf), 
        Point(-inf, inf), 
        Point(-inf, -inf), 
        Point(inf, -inf) 
    };

    for(int i = 0; i<4; i++) { // Add bounding box half-planes.
        Halfplane aux(box[i], box[(i+1) % 4]);
        H.push_back(aux);
    }

    // Sort by angle and start algorithm
    sort(H.begin(), H.end());
    deque<Halfplane> dq;
    int len = 0;
    for(int i = 0; i < int(H.size()); i++) {

        // Remove from the back of the deque while last half-plane is redundant
        while (len > 1 && H[i].out(inter(dq[len-1], dq[len-2]))) {
            dq.pop_back();
            --len;
        }

        // Remove from the front of the deque while first half-plane is redundant
        while (len > 1 && H[i].out(inter(dq[0], dq[1]))) {
            dq.pop_front();
            --len;
        }

        // Special case check: Parallel half-planes
        if (len > 0 && fabsl(cross(H[i].pq, dq[len-1].pq)) < eps) {
            // Opposite parallel half-planes that ended up checked against each other.
            if (dot(H[i].pq, dq[len-1].pq) < 0.0)
                return vector<Point>();

            // Same direction half-plane: keep only the leftmost half-plane.
            if (H[i].out(dq[len-1].p)) {
                dq.pop_back();
                --len;
            }
            else continue;
        }

        // Add new half-plane
        dq.push_back(H[i]);
        ++len;
    }

    // Final cleanup: Check half-planes at the front against the back and vice-versa
    while (len > 2 && dq[0].out(inter(dq[len-1], dq[len-2]))) {
        dq.pop_back();
        --len;
    }

    while (len > 2 && dq[len-1].out(inter(dq[0], dq[1]))) {
        dq.pop_front();
        --len;
    }

    // Report empty intersection if necessary
    if (len < 3) return vector<Point>();

    // Reconstruct the convex polygon from the remaining half-planes.
    vector<Point> ret(len);
    for(int i = 0; i+1 < len; i++) {
        ret[i] = inter(dq[i], dq[i+1]);
    }
    ret.back() = inter(dq[len-1], dq[0]);
    return ret;
}

Thảo luận về cài đặt (Implementation discussion)

Một điều đặc biệt cần lưu ý là, trong trường hợp có nhiều nửa mặt phẳng giao nhau tại cùng một điểm, thì thuật toán này có thể trả về các điểm liền kề lặp lại trong đa giác cuối cùng. Tuy nhiên, điều này sẽ không có bất kỳ tác động nào đến việc đánh giá chính xác xem phần giao có rỗng hay không, và nó cũng không ảnh hưởng đến diện tích đa giác chút nào. Bạn có thể muốn xóa các bản sao này tùy thuộc vào nhiệm vụ bạn cần làm sau đó. Bạn có thể thực hiện việc này rất dễ dàng với std::unique. Chúng tôi muốn giữ các điểm lặp lại trong quá trình thực hiện thuật toán để các giao điểm có diện tích bằng không có thể được tính toán chính xác (ví dụ: các giao điểm bao gồm một điểm, đường thẳng hoặc đoạn thẳng duy nhất). Tôi khuyến khích người đọc kiểm tra một số trường hợp thủ công nhỏ trong đó kết quả giao nhau là một điểm hoặc đường thẳng duy nhất.

Một điều nữa cần được nói đến là phải làm gì nếu chúng ta được cung cấp các nửa mặt phẳng dưới dạng ràng buộc tuyến tính (ví dụ: $ax + by + c \leq 0$). Trong trường hợp như vậy, có hai lựa chọn. Bạn có thể cài đặt thuật toán với các sửa đổi tương ứng để làm việc với biểu diễn như vậy (về cơ bản là tạo struct nửa mặt phẳng của riêng bạn, sẽ khá đơn giản nếu bạn quen thuộc với thủ thuật bao lồi), hoặc bạn có thể chuyển đổi các đường thẳng thành biểu diễn mà chúng tôi đã sử dụng trong bài viết này bằng cách lấy bất kỳ 2 điểm nào của mỗi đường thẳng. Nói chung, nên làm việc với biểu diễn mà bạn được cung cấp trong bài toán để tránh các vấn đề chính xác bổ sung.

Bài toán, nhiệm vụ và ứng dụng (Problems, tasks and applications)

Nhiều bài toán có thể giải được bằng giao điểm nửa mặt phẳng cũng có thể giải được mà không cần nó, nhưng với (thường là) các cách tiếp cận phức tạp hoặc không phổ biến hơn. Nhìn chung, giao điểm nửa mặt phẳng có thể xuất hiện khi xử lý các bài toán liên quan đến đa giác (chủ yếu là lồi), khả năng nhìn thấy trong mặt phẳng và quy hoạch tuyến tính hai chiều. Dưới đây là một số nhiệm vụ mẫu có thể được giải quyết bằng kỹ thuật này:

Giao của đa giác lồi (Convex polygon intersection)

Một trong những ứng dụng cổ điển của giao điểm nửa mặt phẳng: Cho $N$ đa giác, tính toán vùng được bao gồm bên trong tất cả các đa giác.

Vì giao của một tập hợp các nửa mặt phẳng là một đa giác lồi, chúng ta cũng có thể biểu diễn một đa giác lồi dưới dạng một tập hợp các nửa mặt phẳng (mọi cạnh của đa giác là một đoạn của một nửa mặt phẳng). Tạo các nửa mặt phẳng này cho mọi đa giác và tính toán giao của toàn bộ tập hợp. Tổng độ phức tạp thời gian là $O(S \log S)$, trong đó S là tổng số cạnh của tất cả các đa giác. Bài toán về mặt lý thuyết cũng có thể được giải quyết trong $O(S \log N)$ bằng cách hợp nhất $N$ tập hợp các nửa mặt phẳng bằng cách sử dụng heap và sau đó chạy thuật toán mà không cần bước sắp xếp, nhưng giải pháp như vậy có hằng số tồi tệ hơn nhiều so với sắp xếp đơn giản và chỉ cung cấp mức tăng tốc độ nhỏ cho $N$ rất nhỏ.

Khả năng nhìn thấy trong mặt phẳng (Visibility in the plane)

Các bài toán yêu cầu một cái gì đó trong các dòng "xác định xem một số đoạn thẳng có thể nhìn thấy được từ một số điểm trong mặt phẳng hay không" thường có thể được xây dựng dưới dạng các bài toán giao điểm nửa mặt phẳng. Ví dụ, hãy thực hiện nhiệm vụ sau: Cho một đa giác đơn giản (không nhất thiết là lồi), xác định xem có điểm nào bên trong đa giác sao cho toàn bộ biên của đa giác có thể được quan sát từ điểm đó hay không. Điều này còn được gọi là tìm hạt nhân của đa giác (kernel of a polygon) và có thể được giải quyết bằng giao điểm nửa mặt phẳng đơn giản, lấy mỗi cạnh của đa giác làm một nửa mặt phẳng và sau đó tính toán giao điểm của nó.

Dưới đây là một bài toán liên quan, thú vị hơn đã được trình bày bởi Artem Vasilyev trong một trong những bài giảng tại Trường Hè ICPC Brazil của anh ấy: Cho một tập hợp $p$ các điểm $p_1, p_2\ \dots \ p_n$ trong mặt phẳng, xác định xem có bất kỳ điểm $q$ nào bạn có thể đứng tại đó sao cho bạn có thể nhìn thấy tất cả các điểm của $p$ từ trái sang phải theo thứ tự tăng dần của chỉ số của chúng.

Bài toán như vậy có thể giải được bằng cách nhận thấy rằng việc có thể nhìn thấy một điểm $p_i$ nào đó ở bên trái của $p_j$ giống như việc có thể nhìn thấy phía bên phải của đoạn thẳng từ $p_i$ đến $p_j$ (hoặc tương đương, có thể nhìn thấy phía bên trái của đoạn thẳng từ $p_j$ đến $p_i$). Với ý nghĩ đó, chúng ta có thể chỉ cần tạo một nửa mặt phẳng cho mỗi đoạn thẳng $p_i p_{i+1}$ (hoặc $p_{i+1} p_i$ tùy thuộc vào hướng bạn chọn) và kiểm tra xem giao của toàn bộ tập hợp có rỗng hay không.

Một ứng dụng phổ biến khác là sử dụng giao điểm nửa mặt phẳng như một công cụ để xác thực vị ngữ (predicate) của một thủ tục tìm kiếm nhị phân. Dưới đây là một ví dụ về một bài toán như vậy, cũng được trình bày bởi Artem Vasilyev trong cùng bài giảng đã đề cập trước đó: Cho một đa giác lồi $P$, tìm chu vi lớn nhất có thể nội tiếp bên trong nó.

Thay vì tìm kiếm một loại giải pháp dạng đóng, các công thức khó chịu hoặc các giải pháp thuật toán tối nghĩa, thay vào đó hãy thử tìm kiếm nhị phân trên câu trả lời. Lưu ý rằng, đối với một $r$ cố định nào đó, một vòng tròn có bán kính $r$ có thể được nội tiếp bên trong $P$ chỉ khi tồn tại một điểm nào đó bên trong $P$ có khoảng cách lớn hơn hoặc bằng $r$ đến tất cả các điểm biên của $P$. Điều kiện này có thể được xác thực bằng cách "thu nhỏ" đa giác vào trong một khoảng cách $r$ và kiểm tra xem đa giác có còn không suy biến hay không (hoặc bản thân nó là một điểm/đoạn). Quy trình như vậy có thể được mô phỏng bằng cách lấy các nửa mặt phẳng của các cạnh đa giác theo thứ tự ngược chiều kim đồng hồ, dịch chuyển từng cái một khoảng cách $r$ theo hướng của vùng mà chúng cho phép (nghĩa là, trực giao với vector chỉ phương của nửa mặt phẳng), và kiểm tra xem giao điểm có không rỗng hay không.

Rõ ràng, nếu chúng ta có thể nội tiếp một đường tròn có bán kính $r$, chúng ta cũng có thể nội tiếp bất kỳ đường tròn nào khác có bán kính nhỏ hơn $r$. Vì vậy, chúng ta có thể thực hiện tìm kiếm nhị phân trên bán kính $r$ và xác thực từng bước bằng cách sử dụng giao điểm nửa mặt phẳng. Ngoài ra, lưu ý rằng các nửa mặt phẳng của một đa giác lồi đã được sắp xếp theo góc, vì vậy bước sắp xếp có thể được bỏ qua trong thuật toán. Do đó, chúng ta thu được tổng độ phức tạp thời gian là $O(NK)$, trong đó $N$ là số đỉnh đa giác và $K$ là số lần lặp của tìm kiếm nhị phân (giá trị thực tế sẽ phụ thuộc vào phạm vi của các câu trả lời có thể và độ chính xác mong muốn).

Quy hoạch tuyến tính hai chiều (Two-dimensional linear programming)

Một ứng dụng nữa của giao điểm nửa mặt phẳng là quy hoạch tuyến tính trong hai biến. Tất cả các ràng buộc tuyến tính cho hai biến có thể được biểu thị dưới dạng $Ax + By + C \leq 0$ (bộ so sánh bất đẳng thức có thể thay đổi). Rõ ràng, đây chỉ là các nửa mặt phẳng, vì vậy việc kiểm tra xem một giải pháp khả thi có tồn tại cho một tập hợp các ràng buộc tuyến tính hay không có thể được thực hiện bằng giao điểm nửa mặt phẳng. Ngoài ra, đối với một tập hợp các ràng buộc tuyến tính đã cho, có thể tính toán vùng của các giải pháp khả thi (tức là giao của các nửa mặt phẳng) và sau đó trả lời nhiều truy vấn về việc tối đa hóa/tối thiểu hóa một số hàm tuyến tính $f(x, y)$ tuân theo các ràng buộc trong $O(\log N)$ mỗi truy vấn bằng cách sử dụng tìm kiếm nhị phân (rất giống với thủ thuật bao lồi).

Đáng nói đến là cũng tồn tại một thuật toán ngẫu nhiên khá đơn giản có thể kiểm tra xem một tập hợp các ràng buộc tuyến tính có giải pháp khả thi hay không, và tối đa hóa/tối thiểu hóa một số hàm tuyến tính tuân theo các ràng buộc đã cho. Thuật toán ngẫu nhiên này cũng được giải thích độc đáo bởi Artem Vasilyev trong bài giảng đã đề cập trước đó. Dưới đây là một số tài nguyên bổ sung về nó, nếu người đọc quan tâm: CG - Bài giảng 4, phần 4 và 5 và Blog của Petr Mitrichev (bao gồm giải pháp cho bài toán khó nhất trong danh sách bài tập thực hành bên dưới).

Bài tập (Practice problems)

Bài toán kinh điển, ứng dụng trực tiếp

Bài toán khó hơn

Bài toán bổ sung

  • 40th Petrozavodsk Programming Camp, Winter 2021 - Day 1: Jagiellonian U Contest, Grand Prix of Krakow - Problem B: (Almost) Fair Cake-Cutting. Tại thời điểm viết bài, bài toán này là riêng tư và chỉ có thể truy cập bởi những người tham gia Trại Lập trình.

Tài liệu tham khảo, thư mục và các nguồn khác (References, bibliography and other sources)

Nguồn chính

Blog hay (tiếng Trung)

Thuật toán ngẫu nhiên