Cây khung nhỏ nhất - Thuật toán Kruskal (Minimum spanning tree - Kruskal's algorithm)¶

Cho một đồ thị vô hướng có trọng số. Chúng ta muốn tìm một cây con của đồ thị này kết nối tất cả các đỉnh (tức là nó là một cây khung) và có trọng số nhỏ nhất (tức là tổng trọng số của tất cả các cạnh là nhỏ nhất) trong số tất cả các cây khung có thể có. Cây khung này được gọi là cây khung nhỏ nhất (minimum spanning tree).

Trong hình bên trái bạn có thể thấy một đồ thị vô hướng có trọng số, và trong hình bên phải bạn có thể thấy cây khung nhỏ nhất tương ứng.

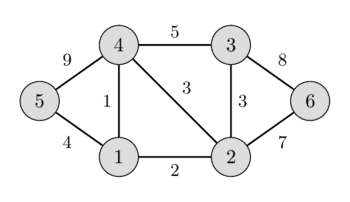
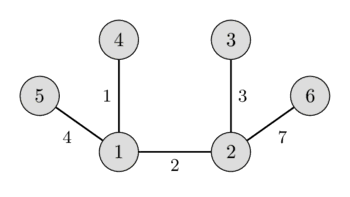
Random graph MST of this graph

Bài viết này sẽ thảo luận về một vài thực tế quan trọng liên quan đến cây khung nhỏ nhất, và sau đó sẽ đưa ra cài đặt đơn giản nhất của thuật toán Kruskal để tìm cây khung nhỏ nhất.

Tính chất của cây khung nhỏ nhất (Properties of the minimum spanning tree)¶

Một cây khung nhỏ nhất của một đồ thị là duy nhất, nếu trọng số của tất cả các cạnh là khác nhau. Ngược lại, có thể có nhiều cây khung nhỏ nhất. (Các thuật toán cụ thể thường xuất ra một trong những cây khung nhỏ nhất có thể).
Cây khung nhỏ nhất cũng là cây có tích các trọng số của các cạnh là nhỏ nhất. (Điều này có thể dễ dàng được chứng minh bằng cách thay thế trọng số của tất cả các cạnh bằng logarit của chúng)
Trong một cây khung nhỏ nhất của một đồ thị, trọng số lớn nhất của một cạnh là nhỏ nhất có thể từ tất cả các cây khung có thể có của đồ thị đó. (Điều này suy ra từ tính đúng đắn của thuật toán Kruskal).
Cây khung lớn nhất (maximum spanning tree) (cây khung với tổng trọng số của các cạnh là lớn nhất) của một đồ thị có thể thu được tương tự như cây khung nhỏ nhất, bằng cách thay đổi dấu của trọng số của tất cả các cạnh thành ngược lại và sau đó áp dụng bất kỳ thuật toán cây khung nhỏ nhất nào.

Thuật toán Kruskal (Kruskal's algorithm)¶

Thuật toán này được mô tả bởi Joseph Bernard Kruskal, Jr. vào năm 1956.

Thuật toán Kruskal ban đầu đặt tất cả các nút của đồ thị ban đầu cô lập với nhau, để tạo thành một rừng các cây nút đơn lẻ, và sau đó dần dần hợp nhất các cây này, kết hợp ở mỗi lần lặp bất kỳ hai trong số tất cả các cây với một cạnh nào đó của đồ thị ban đầu. Trước khi thực hiện thuật toán, tất cả các cạnh được sắp xếp theo trọng số (theo thứ tự không giảm). Sau đó bắt đầu quá trình hợp nhất: chọn tất cả các cạnh từ đầu đến cuối (theo thứ tự đã sắp xếp), và nếu các đầu của cạnh được chọn hiện tại thuộc về các cây con khác nhau, các cây con này được kết hợp, và cạnh được thêm vào câu trả lời. Sau khi lặp qua tất cả các cạnh, tất cả các đỉnh sẽ thuộc về cùng một cây con, và chúng ta sẽ nhận được câu trả lời.

Cài đặt đơn giản nhất (The simplest implementation)¶

Mã sau đây cài đặt trực tiếp thuật toán được mô tả ở trên, và có độ phức tạp thời gian $O(M \log M + N^2)$. Sắp xếp các cạnh yêu cầu $O(M \log N)$ (giống như $O(M \log M)$) thao tác. Thông tin liên quan đến cây con mà một đỉnh thuộc về được duy trì với sự trợ giúp của một mảng tree_id[] - đối với mỗi đỉnh v, tree_id[v] lưu trữ số của cây, mà v thuộc về. Đối với mỗi cạnh, liệu nó có thuộc về các đầu của các cây khác nhau hay không, có thể được xác định trong $O(1)$. Cuối cùng, sự hợp nhất của hai cây được thực hiện trong $O(N)$ bằng một lần duyệt đơn giản qua mảng tree_id[]. Giả sử rằng tổng số thao tác hợp nhất là $N-1$, chúng ta thu được hành vi tiệm cận của $O(M \log N + N^2)$.

struct Edge {
    int u, v, weight;
    bool operator<(Edge const& other) {
        return weight < other.weight;
    }
};

int n;
vector<Edge> edges;

int cost = 0;
vector<int> tree_id(n);
vector<Edge> result;
for (int i = 0; i < n; i++)
    tree_id[i] = i;

sort(edges.begin(), edges.end());

for (Edge e : edges) {
    if (tree_id[e.u] != tree_id[e.v]) {
        cost += e.weight;
        result.push_back(e);

        int old_id = tree_id[e.u], new_id = tree_id[e.v];
        for (int i = 0; i < n; i++) {
            if (tree_id[i] == old_id)
                tree_id[i] = new_id;
        }
    }
}

Chứng minh tính đúng đắn (Proof of correctness)¶

Tại sao thuật toán Kruskal cho chúng ta kết quả chính xác?

Nếu đồ thị ban đầu liên thông, thì đồ thị kết quả cũng sẽ liên thông. Bởi vì nếu không sẽ có hai thành phần có thể được kết nối với ít nhất một cạnh. Mặc dù điều này là không thể, bởi vì Kruskal sẽ chọn một trong những cạnh này, vì id của các thành phần là khác nhau. Ngoài ra đồ thị kết quả không chứa bất kỳ chu trình nào, vì chúng ta cấm điều này một cách rõ ràng trong thuật toán. Do đó thuật toán tạo ra một cây khung.

Vậy tại sao thuật toán này cho chúng ta một cây khung nhỏ nhất?

Chúng ta có thể chỉ ra đề xuất "nếu $F$ là một tập hợp các cạnh được chọn bởi thuật toán ở bất kỳ giai đoạn nào trong thuật toán, thì tồn tại một MST chứa tất cả các cạnh của $F$" bằng quy nạp.

Đề xuất rõ ràng là đúng ở lúc bắt đầu, tập hợp rỗng là một tập hợp con của bất kỳ MST nào.

Bây giờ giả sử $F$ là một tập hợp cạnh nào đó ở bất kỳ giai đoạn nào của thuật toán, $T$ là một MST chứa $F$ và $e$ là cạnh mới chúng ta muốn thêm bằng Kruskal.

Nếu $e$ tạo ra một chu trình, thì chúng ta không thêm nó, và vì vậy đề xuất vẫn đúng sau bước này.

Trong trường hợp $T$ đã chứa $e$, đề xuất cũng đúng sau bước này.

Trong trường hợp $T$ không chứa cạnh $e$, thì $T + e$ sẽ chứa một chu trình $C$. Chu trình này sẽ chứa ít nhất một cạnh $f$, không nằm trong $F$. Tập hợp các cạnh $T - f + e$ cũng sẽ là một cây khung. Lưu ý rằng trọng số của $f$ không thể nhỏ hơn trọng số của $e$, bởi vì nếu không Kruskal đã chọn $f$ sớm hơn. Nó cũng không thể có trọng số lớn hơn, vì điều đó sẽ làm cho tổng trọng số của $T - f + e$ nhỏ hơn tổng trọng số của $T$, điều này là không thể vì $T$ đã là một MST. Điều này có nghĩa là trọng số của $e$ phải giống như trọng số của $f$. Do đó $T - f + e$ cũng là một MST, và nó chứa tất cả các cạnh từ $F + e$. Vì vậy ở đây đề xuất cũng vẫn được hoàn thành sau bước này.

Điều này chứng minh đề xuất. Điều đó có nghĩa là sau khi lặp qua tất cả các cạnh, tập hợp cạnh kết quả sẽ liên thông, và sẽ được chứa trong một MST, điều đó có nghĩa là nó đã phải là một MST rồi.

Cài đặt cải tiến (Improved implementation)¶

Chúng ta có thể sử dụng cấu trúc dữ liệu Disjoint Set Union (DSU) để viết một bản cài đặt nhanh hơn của thuật toán Kruskal với độ phức tạp thời gian khoảng $O(M \log N)$. Bài viết này trình bày chi tiết về cách tiếp cận như vậy.