Cây Fenwick (Fenwick Tree)¶

Giả sử $f$ là một phép toán nhóm (một hàm kết hợp hai ngôi trên một tập hợp với một phần tử đơn vị và các phần tử nghịch đảo) và $A$ là một mảng các số nguyên có độ dài $N$. Ký hiệu trung tố của $f$ là $*$; nghĩa là, $f(x,y) = x*y$ với các số nguyên $x,y$ bất kỳ. (Vì phép toán này có tính chất kết hợp, chúng ta sẽ bỏ qua các dấu ngoặc đơn cho thứ tự áp dụng của $f$ khi sử dụng ký hiệu trung tố.)

Cây Fenwick là một cấu trúc dữ liệu mà:

tính toán giá trị của hàm $f$ trong đoạn đã cho $[l, r]$ (tức là $A_l * A_{l+1} * \dots * A_r$) trong thời gian $O(\log N)$
cập nhật giá trị của một phần tử của $A$ trong thời gian $O(\log N)$
yêu cầu bộ nhớ $O(N)$ (cùng một lượng cần thiết cho $A$)
dễ sử dụng và lập trình, đặc biệt là trong trường hợp mảng nhiều chiều

Uứng dụng phổ biến nhất của cây Fenwick là tính tổng của một đoạn. Ví dụ, sử dụng phép cộng trên tập hợp các số nguyên làm phép toán nhóm, tức là $f(x,y) = x + y$: phép toán hai ngôi, $*$, là $+$ trong trường hợp này, vì vậy $A_l * A_{l+1} * \dots * A_r = A_l + A_{l+1} + \dots + A_{r}$.

Cây Fenwick còn được gọi là Cây chỉ số nhị phân (Binary Indexed Tree - BIT). Nó được mô tả lần đầu tiên trong một bài báo có tiêu đề "A new data structure for cumulative frequency tables" (Peter M. Fenwick, 1994).

Mô tả (Description)¶

Tổng quan (Overview)¶

Để đơn giản, chúng ta sẽ giả định rằng hàm $f$ được định nghĩa là $f(x,y) = x + y$ trên các số nguyên.

Giả sử chúng ta được cho một mảng các số nguyên, $A[0 \dots N-1]$. (Lưu ý rằng chúng ta đang sử dụng chỉ số bắt đầu từ 0.) Cây Fenwick chỉ là một mảng, $T[0 \dots N-1]$, trong đó mỗi phần tử bằng tổng các phần tử của $A$ trong một số đoạn, $[g(i), i]$:

$$T_i = \sum_{j = g(i)}^{i}{A_j}$$

trong đó $g$ là một hàm nào đó thỏa mãn $0 \le g(i) \le i$. Chúng ta sẽ định nghĩa $g$ trong một vài đoạn tiếp theo.

Cấu trúc dữ liệu được gọi là cây vì có một biểu diễn đẹp của nó dưới dạng cây, mặc dù chúng ta không cần lập mô hình một cây thực tế với các nút và cạnh. Chúng ta chỉ cần duy trì mảng $T$ để xử lý tất cả các truy vấn.

Lưu ý: Cây Fenwick được trình bày ở đây sử dụng chỉ số bắt đầu từ 0. Nhiều người sử dụng một phiên bản của cây Fenwick sử dụng chỉ số bắt đầu từ 1. Do đó, bạn cũng sẽ tìm thấy một triển khai thay thế sử dụng chỉ số bắt đầu từ 1 trong phần cài đặt. Cả hai phiên bản đều tương đương về độ phức tạp thời gian và bộ nhớ.

Bây giờ chúng ta có thể viết một số mã giả cho hai thao tác được đề cập ở trên. Dưới đây, chúng ta nhận tổng các phần tử của $A$ trong đoạn $[0, r]$ và cập nhật (tăng) một số phần tử $A_i$:

def sum(int r):
    res = 0
    while (r >= 0):
        res += t[r]
        r = g(r) - 1
    return res

def increase(int i, int delta):
    for all j with g(j) <= i <= j:
        t[j] += delta

Hàm sum hoạt động như sau:

Đầu tiên, nó thêm tổng của đoạn $[g(r), r]$ (tức là $T[r]$) vào result.
Sau đó, nó "nhảy" đến đoạn $[g(g(r)-1), g(r)-1]$ và thêm tổng của đoạn này vào result.
Điều này tiếp tục cho đến khi nó "nhảy" từ $[0, g(g( \dots g(r)-1 \dots -1)-1)]$ đến $[g(-1), -1]$; đây là nơi hàm sum ngừng nhảy.

Hàm increase hoạt động với sự tương tự, nhưng nó "nhảy" theo hướng tăng chỉ số:

Tổng cho mỗi đoạn có dạng $[g(j), j]$ thỏa mãn điều kiện $g(j) \le i \le j$ được tăng thêm delta; nghĩa là, t[j] += delta. Do đó, nó cập nhật tất cả các phần tử trong $T$ tương ứng với các đoạn mà $A_i$ nằm trong đó.

Độ phức tạp của cả sum và increase phụ thuộc vào hàm $g$. Có nhiều cách để chọn hàm $g$ sao cho $0 \le g(i) \le i$ cho tất cả $i$. Ví dụ, hàm $g(i) = i$ hoạt động, mang lại $T = A$ (trong trường hợp này, các truy vấn tính tổng chậm). Chúng ta cũng có thể lấy hàm $g(i) = 0$. Điều này sẽ tương ứng với các mảng tổng tiền tố (trong trường hợp này, việc tìm tổng của đoạn $[0, i]$ sẽ chỉ mất thời gian hằng số; tuy nhiên, các cập nhật chậm). Phần thông minh của thuật toán cho cây Fenwick là cách nó sử dụng một định nghĩa đặc biệt của hàm $g$ có thể xử lý cả hai thao tác trong thời gian $O(\log N)$.

Định nghĩa của $g(i)$ (Definition of g(i))¶

Việc tính toán $g(i)$ được xác định bằng cách sử dụng thao tác đơn giản sau: chúng ta thay thế tất cả các bit $1$ ở cuối trong biểu diễn nhị phân của $i$ bằng các bit $0$.

Nói cách khác, nếu chữ số có nghĩa nhỏ nhất của $i$ trong hệ nhị phân là $0$, thì $g(i) = i$. Và ngược lại, chữ số có nghĩa nhỏ nhất là $1$, và chúng ta lấy $1$ này và tất cả các số $1$ ở cuối khác và lật chúng.

Ví dụ chúng ta nhận được

$$\begin{align} g(11) = g(1011_2) = 1000_2 &= 8 \\\\ g(12) = g(1100_2) = 1100_2 &= 12 \\\\ g(13) = g(1101_2) = 1100_2 &= 12 \\\\ g(14) = g(1110_2) = 1110_2 &= 14 \\\\ g(15) = g(1111_2) = 0000_2 &= 0 \\\\ \end{align}$$

Tồn tại một cách cài đặt đơn giản bằng cách sử dụng các phép toán bit cho thao tác không tầm thường được mô tả ở trên:

$$g(i) = i ~\&~ (i+1),$$

trong đó $\&$ là toán tử AND bit. Không khó để thuyết phục bản thân rằng giải pháp này thực hiện điều tương tự như thao tác được mô tả ở trên.

Bây giờ, chúng ta chỉ cần tìm một cách để lặp lại tất cả các $j$, sao cho $g(j) \le i \le j$.

Dễ thấy rằng chúng ta có thể tìm thấy tất cả các $j$ như vậy bằng cách bắt đầu với $i$ và lật bit chưa được đặt cuối cùng. Chúng ta sẽ gọi thao tác này là $h(j)$. Ví dụ, đối với $i = 10$ chúng ta có:

$$\begin{align} 10 &= 0001010_2 \\\\ h(10) = 11 &= 0001011_2 \\\\ h(11) = 15 &= 0001111_2 \\\\ h(15) = 31 &= 0011111_2 \\\\ h(31) = 63 &= 0111111_2 \\\\ \vdots & \end{align}$$

Không có gì ngạc nhiên, cũng tồn tại một cách đơn giản để thực hiện $h$ bằng cách sử dụng các phép toán bit:

$$h(j) = j ~|~ (j+1),$$

trong đó $|$ là toán tử OR bit.

Hình ảnh sau đây cho thấy một cách giải thích có thể có của cây Fenwick dưới dạng cây. Các nút của cây hiển thị các phạm vi chúng bao phủ.

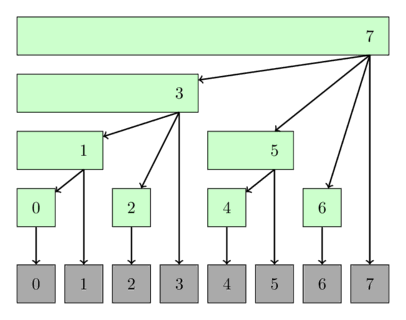
Cài đặt (Implementation)¶

Tìm tổng trong mảng một chiều (Finding sum in one-dimensional array)¶

Ở đây chúng tôi trình bày một cài đặt của cây Fenwick cho các truy vấn tổng và cập nhật đơn lẻ.

Cây Fenwick bình thường chỉ có thể trả lời các truy vấn tổng của loại $[0, r]$ bằng cách sử dụng sum(int r), tuy nhiên chúng ta cũng có thể trả lời các truy vấn khác của loại $[l, r]$ bằng cách tính hai tổng $[0, r]$ và $[0, l-1]$ và trừ chúng. Điều này được xử lý trong phương thức sum(int l, int r).

Ngoài ra việc cài đặt này hỗ trợ hai hàm tạo. Bạn có thể tạo một cây Fenwick được khởi tạo bằng các số không, hoặc bạn có thể chuyển đổi một mảng hiện có thành dạng Fenwick.

fenwick_sum

struct FenwickTree {
    vector<int> bit;  // binary indexed tree
    int n;

    FenwickTree(int n) {
        this->n = n;
        bit.assign(n, 0);
    }

    FenwickTree(vector<int> const &a) : FenwickTree(a.size()) {
        for (size_t i = 0; i < a.size(); i++)
            add(i, a[i]);
    }

    int sum(int r) {
        int ret = 0;
        for (; r >= 0; r = (r & (r + 1)) - 1)
            ret += bit[r];
        return ret;
    }

    int sum(int l, int r) {
        return sum(r) - sum(l - 1);
    }

    void add(int idx, int delta) {
        for (; idx < n; idx = idx | (idx + 1))
            bit[idx] += delta;
    }
};

Xây dựng tuyến tính (Linear construction)¶

Việc cài đặt trên yêu cầu thời gian $O(N \log N)$. Có thể cải thiện điều đó thành thời gian $O(N)$.

Ý tưởng là, số $a[i]$ tại chỉ mục $i$ sẽ đóng góp vào phạm vi được lưu trữ trong $bit[i]$, và cho tất cả các phạm vi mà chỉ mục $i | (i + 1)$ đóng góp vào. Vì vậy, bằng cách thêm các số theo thứ tự, bạn chỉ cần đẩy tổng hiện tại xa hơn sang phạm vi tiếp theo, nơi nó sau đó sẽ được đẩy xa hơn sang phạm vi tiếp theo, v.v.

FenwickTree(vector<int> const &a) : FenwickTree(a.size()){
    for (int i = 0; i < n; i++) {
        bit[i] += a[i];
        int r = i | (i + 1);
        if (r < n) bit[r] += bit[i];
    }
}

Tìm giá trị nhỏ nhất của $[0, r]$ trong mảng một chiều (Finding minimum of [0, r] in one-dimensional array)¶

Rõ ràng là không có cách dễ dàng để tìm giá trị nhỏ nhất của đoạn $[l, r]$ bằng cây Fenwick, vì cây Fenwick chỉ có thể trả lời các truy vấn loại $[0, r]$. Ngoài ra, mỗi khi một giá trị được update (cập nhật), giá trị mới phải nhỏ hơn giá trị hiện tại. Cả hai hạn chế đáng kể là do thao tác $min$ cùng với tập hợp các số nguyên không tạo thành một nhóm, vì không có phần tử nghịch đảo.

fenwick_min

struct FenwickTreeMin {
    vector<int> bit;
    int n;
    const int INF = (int)1e9;

    FenwickTreeMin(int n) {
        this->n = n;
        bit.assign(n, INF);
    }

    FenwickTreeMin(vector<int> a) : FenwickTreeMin(a.size()) {
        for (size_t i = 0; i < a.size(); i++)
            update(i, a[i]);
    }

    int getmin(int r) {
        int ret = INF;
        for (; r >= 0; r = (r & (r + 1)) - 1)
            ret = min(ret, bit[r]);
        return ret;
    }

    void update(int idx, int val) {
        for (; idx < n; idx = idx | (idx + 1))
            bit[idx] = min(bit[idx], val);
    }
};

Lưu ý: có thể cài đặt một cây Fenwick có thể xử lý các truy vấn phạm vi tối thiểu tùy ý và các cập nhật tùy ý. Bài báo Truy vấn phạm vi tối thiểu hiệu quả sử dụng Cây chỉ số nhị phân mô tả một cách tiếp cận như vậy. Tuy nhiên, với cách tiếp cận đó, bạn cần duy trì một cây chỉ số nhị phân thứ hai trên dữ liệu, với cấu trúc hơi khác, vì một cây là không đủ để lưu trữ giá trị của tất cả các phần tử trong mảng. Việc cài đặt cũng khó hơn nhiều so với việc cài đặt bình thường cho tổng.

Tìm tổng trong mảng hai chiều (Finding sum in two-dimensional array)¶

Như đã tuyên bố trước đây, rất dễ dàng để cài đặt Cây Fenwick cho mảng nhiều chiều.

struct FenwickTree2D {
    vector<vector<int>> bit;
    int n, m;

    // init(...) { ... }

    int sum(int x, int y) {
        int ret = 0;
        for (int i = x; i >= 0; i = (i & (i + 1)) - 1)
            for (int j = y; j >= 0; j = (j & (j + 1)) - 1)
                ret += bit[i][j];
        return ret;
    }

    void add(int x, int y, int delta) {
        for (int i = x; i < n; i = i | (i + 1))
            for (int j = y; j < m; j = j | (j + 1))
                bit[i][j] += delta;
    }
};

Cách tiếp cận chỉ số bắt đầu từ 1 (One-based indexing approach)¶

Đối với cách tiếp cận này, chúng ta thay đổi các yêu cầu và định nghĩa cho $T[]$ và $g()$ một chút. Chúng ta muốn $T[i]$ lưu trữ tổng của $[g(i)+1; i]$. Điều này thay đổi việc cài đặt một chút, và cho phép một định nghĩa đẹp tương tự cho $g(i)$:

def sum(int r):
    res = 0
    while (r > 0):
        res += t[r]
        r = g(r)
    return res

def increase(int i, int delta):
    for all j with g(j) < i <= j:
        t[j] += delta

Việc tính toán $g(i)$ được xác định là: lật bit $1$ được đặt cuối cùng trong biểu diễn nhị phân của $i$.

$$\begin{align} g(7) = g(111_2) = 110_2 &= 6 \\\\ g(6) = g(110_2) = 100_2 &= 4 \\\\ g(4) = g(100_2) = 000_2 &= 0 \\\\ \end{align}$$

Bit được đặt cuối cùng có thể được trích xuất bằng cách sử dụng $i ~\&~ (-i)$, vì vậy thao tác có thể được biểu thị là:

$$g(i) = i - (i ~\&~ (-i)).$$

Và không khó để thấy, rằng bạn cần thay đổi tất cả các giá trị $T[j]$ trong chuỗi $i,~ h(i),~ h(h(i)),~ \dots$ khi bạn muốn cập nhật $A[j]$, trong đó $h(i)$ được định nghĩa là:

$$h(i) = i + (i ~\&~ (-i)).$$

Như bạn có thể thấy, lợi ích chính của cách tiếp cận này là các hoạt động nhị phân bổ sung cho nhau rất tốt.

Việc cài đặt sau đây có thể được sử dụng giống như các cài đặt khác, tuy nhiên nó sử dụng lập chỉ mục dựa trên một trong nội bộ.

fenwick_sum_onebased

struct FenwickTreeOneBasedIndexing {
    vector<int> bit;  // binary indexed tree
    int n;

    FenwickTreeOneBasedIndexing(int n) {
        this->n = n + 1;
        bit.assign(n + 1, 0);
    }

    FenwickTreeOneBasedIndexing(vector<int> a)
        : FenwickTreeOneBasedIndexing(a.size()) {
        for (size_t i = 0; i < a.size(); i++)
            add(i, a[i]);
    }

    int sum(int idx) {
        int ret = 0;
        for (++idx; idx > 0; idx -= idx & -idx)
            ret += bit[idx];
        return ret;
    }

    int sum(int l, int r) {
        return sum(r) - sum(l - 1);
    }

    void add(int idx, int delta) {
        for (++idx; idx < n; idx += idx & -idx)
            bit[idx] += delta;
    }
};

Các thao tác trên đoạn (Range operations)¶

Một cây Fenwick có thể hỗ trợ các thao tác phạm vi sau:

Cập nhật điểm và Truy vấn đoạn (Point Update and Range Query)
Cập nhật đoạn và Truy vấn điểm (Range Update and Point Query)
Cập nhật đoạn và Truy vấn đoạn (Range Update and Range Query)

1. Cập nhật điểm và Truy vấn đoạn¶

Đây chỉ là cây Fenwick bình thường như đã giải thích ở trên.

2. Cập nhật đoạn và Truy vấn điểm¶

Sử dụng các thủ thuật đơn giản, chúng ta cũng có thể thực hiện các thao tác ngược lại: tăng phạm vi và truy vấn các giá trị đơn lẻ.

Hãy để cây Fenwick được khởi tạo với các số không. Giả sử rằng chúng ta muốn tăng khoảng $[l, r]$ thêm $x$. Chúng ta thực hiện hai thao tác cập nhật điểm trên cây Fenwick là add(l, x) và add(r+1, -x).

Nếu chúng ta muốn nhận giá trị của $A[i]$, chúng ta chỉ cần lấy tổng tiền tố bằng phương pháp tổng phạm vi thông thường. Để xem tại sao điều này đúng, chúng ta có thể tập trung vào thao tác tăng trước đó một lần nữa. Nếu $i < l$, thì hai thao tác cập nhật không ảnh hưởng đến truy vấn và chúng ta nhận được tổng $0$. Nếu $i \in [l, r]$, thì chúng ta nhận được câu trả lời $x$ vì thao tác cập nhật đầu tiên. Và nếu $i > r$, thì thao tác cập nhật thứ hai sẽ hủy bỏ tác dụng của thao tác đầu tiên.

Việc cài đặt sau đây sử dụng chỉ số bắt đầu từ 1.

void add(int idx, int val) {
    for (++idx; idx < n; idx += idx & -idx)
        bit[idx] += val;
}

void range_add(int l, int r, int val) {
    add(l, val);
    add(r + 1, -val);
}

int point_query(int idx) {
    int ret = 0;
    for (++idx; idx > 0; idx -= idx & -idx)
        ret += bit[idx];
    return ret;
}

Lưu ý: tất nhiên cũng có thể tăng một điểm đơn lẻ $A[i]$ với range_add(i, i, val).

3. Cập nhật đoạn và Truy vấn đoạn¶

Để hỗ trợ cả cập nhật phạm vi và truy vấn phạm vi, chúng ta sẽ sử dụng hai BIT cụ thể là $B_1[]$ và $B_2[]$, được khởi tạo bằng các số không.

Giả sử rằng chúng ta muốn tăng khoảng $[l, r]$ thêm giá trị $x$. Tương tự như trong phương pháp trước, chúng ta thực hiện hai cập nhật điểm trên $B_1$: add(B1, l, x) và add(B1, r+1, -x). Và chúng ta cũng cập nhật $B_2$. Các chi tiết sẽ được giải thích sau.

def range_add(l, r, x):
    add(B1, l, x)
    add(B1, r+1, -x)
    add(B2, l, x*(l-1))
    add(B2, r+1, -x*r))

Sau khi cập nhật phạm vi $(l, r, x)$ truy vấn tổng phạm vi sẽ trả về các giá trị sau:

$$ sum[0, i]= \begin{cases} 0 & i < l \\\\ x \cdot (i-(l-1)) & l \le i \le r \\\\ x \cdot (r-l+1) & i > r \\\\ \end{cases} $$

Chúng ta có thể viết tổng phạm vi dưới chênh lệch của hai số hạng, trong đó chúng ta sử dụng $B_1$ cho số hạng đầu tiên và $B_2$ cho số hạng thứ hai. Sự khác biệt của các truy vấn sẽ cho chúng ta tổng tiền tố trên $[0, i]$.

$$\begin{align} sum[0, i] &= sum(B_1, i) \cdot i - sum(B_2, i) \\\\ &= \begin{cases} 0 \cdot i - 0 & i < l\\\\ x \cdot i - x \cdot (l-1) & l \le i \le r \\\\ 0 \cdot i - (x \cdot (l-1) - x \cdot r) & i > r \\\\ \end{cases} \end{align} $$

Biểu thức cuối cùng chính xác bằng các thuật ngữ được yêu cầu. Do đó, chúng ta có thể sử dụng $B_2$ để loại bỏ các số hạng thừa khi chúng ta nhân $B_1[i]\times i$.

Chúng ta có thể tìm tổng phạm vi tùy ý bằng cách tính tổng tiền tố cho $l-1$ và $r$ và lấy hiệu của chúng một lần nữa.

def add(b, idx, x):
    while idx <= N:
        b[idx] += x
        idx += idx & -idx

def range_add(l,r,x):
    add(B1, l, x)
    add(B1, r+1, -x)
    add(B2, l, x*(l-1))
    add(B2, r+1, -x*r)

def sum(b, idx):
    total = 0
    while idx > 0:
        total += b[idx]
        idx -= idx & -idx
    return total

def prefix_sum(idx):
    return sum(B1, idx)*idx -  sum(B2, idx)

def range_sum(l, r):
    return prefix_sum(r) - prefix_sum(l-1)