Cấu trúc dữ liệu các tập hợp rời nhau (Disjoint Set Union)¶
Bài viết này thảo luận về cấu trúc dữ liệu Các tập hợp rời nhau (Disjoint Set Union) hoặc DSU. Thông thường, nó cũng được gọi là Union Find (Hợp-Tìm) vì hai hoạt động chính của nó.
Cấu trúc dữ liệu này cung cấp các khả năng sau. Chúng ta được cho một số phần tử, mỗi phần tử là một tập hợp riêng biệt. Một DSU sẽ có một thao tác để kết hợp hai tập hợp bất kỳ, và nó sẽ có thể cho biết phần tử cụ thể nằm trong tập hợp nào. Phiên bản cổ điển cũng giới thiệu thao tác thứ ba, nó có thể tạo một tập hợp từ một phần tử mới.
Do đó, giao diện cơ bản của cấu trúc dữ liệu này chỉ bao gồm ba thao tác:
make_set(v)- tạo một tập hợp mới bao gồm phần tử mớivunion_sets(a, b)- hợp nhất hai tập hợp đã chỉ định (tập hợp chứa phần tửa, và tập hợp chứa phần tửb)find_set(v)- trả về đại diện (còn gọi là lãnh đạo) của tập hợp chứa phần tửv. Đại diện này là một phần tử của tập hợp tương ứng của nó. Nó được chọn trong mỗi tập hợp bởi chính cấu trúc dữ liệu (và có thể thay đổi theo thời gian, cụ thể là sau các lệnh gọiunion_sets). Đại diện này có thể được sử dụng để kiểm tra xem hai phần tử có thuộc cùng một tập hợp hay không.avàbchính xác trong cùng một tập hợp, nếufind_set(a) == find_set(b). Ngược lại chúng ở trong các tập hợp khác nhau.
Như được mô tả chi tiết hơn sau này, cấu trúc dữ liệu cho phép bạn thực hiện từng thao tác này trong thời gian trung bình gần như $O(1)$.
Cũng trong một trong các tiểu mục, một cấu trúc thay thế của DSU được giải thích, đạt được độ phức tạp trung bình chậm hơn là $O(\log n)$, nhưng có thể mạnh hơn cấu trúc DSU thông thường.
Xây dựng cấu trúc dữ liệu hiệu quả (Build an efficient data structure)¶
Chúng ta sẽ lưu trữ các tập hợp dưới dạng cây (trees): mỗi cây sẽ tương ứng với một tập hợp. Và gốc của cây sẽ là đại diện/lãnh đạo của tập hợp.
Trong hình ảnh sau đây, bạn có thể thấy biểu diễn của các cây như vậy.
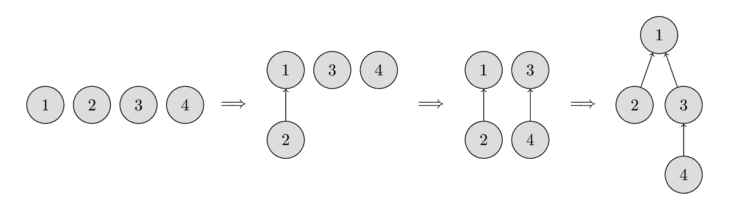
Ban đầu, mỗi phần tử bắt đầu như một tập hợp đơn lẻ, do đó mỗi đỉnh là cây của riêng nó. Sau đó, chúng ta kết hợp tập hợp chứa phần tử 1 và tập hợp chứa phần tử 2. Sau đó, chúng ta kết hợp tập hợp chứa phần tử 3 và tập hợp chứa phần tử 4. Và trong bước cuối cùng, chúng ta kết hợp tập hợp chứa phần tử 1 và tập hợp chứa phần tử 3.
Đối với việc cài đặt, điều này có nghĩa là chúng ta sẽ phải duy trì một mảng parent lưu trữ một tham chiếu đến tổ tiên trực tiếp của nó trong cây.
Cài đặt ngây thơ (Naive implementation)¶
Chúng ta đã có thể viết bản cài đặt đầu tiên của cấu trúc dữ liệu Disjoint Set Union. Lúc đầu nó sẽ khá kém hiệu quả, nhưng sau đó chúng ta có thể cải thiện nó bằng cách sử dụng hai tối ưu hóa, để nó sẽ mất thời gian gần như hằng số cho mỗi lần gọi hàm.
Như chúng ta đã nói, tất cả thông tin về các tập hợp phần tử sẽ được lưu giữ trong một mảng parent.
Để tạo một tập hợp mới (thao tác make_set(v)), chúng ta chỉ cần tạo một cây có gốc tại đỉnh v, nghĩa là nó là tổ tiên của chính nó.
Để kết hợp hai tập hợp (thao tác union_sets(a, b)), trước tiên chúng ta tìm đại diện của tập hợp chứa a, và đại diện của tập hợp chứa b.
Nếu các đại diện giống nhau, chúng ta không có gì để làm, các bộ đã được hợp nhất.
Ngược lại, chúng ta có thể chỉ định đơn giản rằng một trong những đại diện là cha của đại diện kia - do đó kết hợp hai cây.
Cuối cùng là việc cài đặt chức năng tìm đại diện (thao tác find_set(v)):
chúng ta chỉ cần leo lên các tổ tiên của đỉnh v cho đến khi chúng ta đến gốc, tức là một đỉnh sao cho tham chiếu đến tổ tiên dẫn đến chính nó.
Hoạt động này được thực hiện dễ dàng bằng đệ quy.
void make_set(int v) {
parent[v] = v;
}
int find_set(int v) {
if (v == parent[v])
return v;
return find_set(parent[v]);
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b)
parent[b] = a;
}
Tuy nhiên, việc cài đặt này không hiệu quả.
Thật dễ dàng để xây dựng một ví dụ, sao cho các cây thoái hóa thành các chuỗi dài.
Trong trường hợp đó, mỗi lệnh gọi find_set(v) có thể mất thời gian $O(n)$.
Điều này còn xa độ phức tạp mà chúng ta muốn có (thời gian gần như hằng số). Do đó, chúng ta sẽ xem xét hai tối ưu hóa sẽ cho phép tăng tốc đáng kể công việc.
Tối ưu hóa nén đường (Path compression optimization)¶
Tối ưu hóa này được thiết kế để tăng tốc find_set.
Nếu chúng ta gọi find_set(v) cho một số đỉnh v, chúng ta thực sự tìm thấy đại diện p cho tất cả các đỉnh mà chúng ta truy cập trên đường đi giữa v và đại diện thực tế p.
Thủ thuật là làm cho các đường dẫn cho tất cả các nút đó ngắn hơn, bằng cách đặt cha của mỗi đỉnh được truy cập trực tiếp thành p.
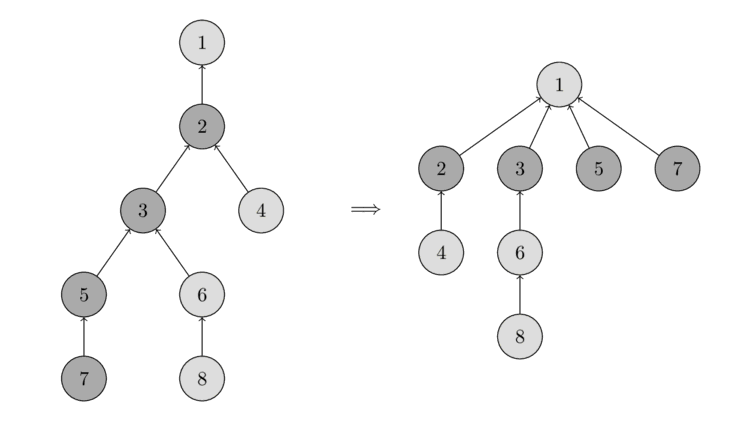
Bạn có thể thấy thao tác trong hình sau.
Bên trái có một cái cây, và bên phải có cây nén sau khi gọi find_set(7), làm ngắn đường dẫn cho các nút đã truy cập 7, 5, 3 và 2.
Việc cài đặt mới của find_set như sau:
int find_set(int v) {
if (v == parent[v])
return v;
return parent[v] = find_set(parent[v]);
}
Việc cài đặt đơn giản thực hiện những gì đã định: đầu tiên tìm đại diện của tập hợp (đỉnh gốc), và sau đó trong quá trình tháo ngăn xếp (stack unwinding), các nút được truy cập được gắn trực tiếp vào đại diện.
Sửa đổi đơn giản này của thao tác đã đạt được độ phức tạp thời gian trung bình $O(\log n)$ mỗi lần gọi (ở đây không có chứng minh). Có một sửa đổi thứ hai, sẽ làm cho nó nhanh hơn nữa.
Hợp nhất theo kích thước / hạng (Union by size / rank)¶
Trong tối ưu hóa này, chúng ta sẽ thay đổi thao tác union_set.
Chính xác hơn, chúng ta sẽ thay đổi cây nào được gắn vào cây kia.
Trong cách cài đặt ngây thơ, cây thứ hai luôn được gắn vào cây thứ nhất.
Trong thực tế, điều đó có thể dẫn đến các cây chứa chuỗi có độ dài $O(n)$.
Với sự tối ưu hóa này, chúng ta sẽ tránh điều này bằng cách chọn rất cẩn thận cây nào được gắn vào.
Có nhiều heuristic có thể được sử dụng. Phổ biến nhất là hai cách tiếp cận sau: Trong cách tiếp cận đầu tiên, chúng ta sử dụng kích thước của cây làm thứ hạng (rank), và trong cách thứ hai, chúng ta sử dụng độ sâu của cây (chính xác hơn là giới hạn trên của độ sâu cây, vì độ sâu sẽ nhỏ hơn khi áp dụng nén đường).
Trong cả hai phương pháp, bản chất của sự tối ưu hóa là giống nhau: chúng ta gắn cây có thứ hạng thấp hơn vào cây có thứ hạng lớn hơn.
Dưới đây là cài đặt hợp nhất theo kích thước:
void make_set(int v) {
parent[v] = v;
size[v] = 1;
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (size[a] < size[b])
swap(a, b);
parent[b] = a;
size[a] += size[b];
}
}
Và đây là việc cài đặt hợp nhất theo hạng dựa trên độ sâu của cây:
void make_set(int v) {
parent[v] = v;
rank[v] = 0;
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (rank[a] < rank[b])
swap(a, b);
parent[b] = a;
if (rank[a] == rank[b])
rank[a]++;
}
}
Độ phức tạp thời gian (Time complexity)¶
Như đã đề cập trước đây, nếu chúng ta kết hợp cả hai tối ưu hóa - nén đường với hợp nhất theo kích thước / hạng - chúng ta sẽ đạt được các truy vấn thời gian gần như hằng số. Hóa ra, độ phức tạp thời gian khấu hao cuối cùng là $O(\alpha(n))$, trong đó $\alpha(n)$ là hàm Ackermann nghịch đảo, phát triển rất chậm. Trên thực tế nó phát triển chậm đến mức, nó không vượt quá $4$ cho tất cả các $n$ hợp lý (khoảng $n < 10^{600}$).
Độ phức tạp khấu hao là tổng thời gian cho mỗi hoạt động, được đánh giá qua một chuỗi nhiều hoạt động. Ý tưởng là đảm bảo tổng thời gian của toàn bộ chuỗi, trong khi cho phép các hoạt động đơn lẻ chậm hơn nhiều so với thời gian khấu hao. Ví dụ: trong trường hợp của chúng ta, một cuộc gọi đơn lẻ có thể mất $O(\log n)$ trong trường hợp xấu nhất, nhưng nếu chúng ta thực hiện $m$ cuộc gọi như vậy liên tiếp, chúng ta sẽ kết thúc với thời gian trung bình là $O(\alpha(n))$.
Chúng tôi cũng sẽ không trình bày bằng chứng cho độ phức tạp thời gian này, vì nó khá dài và phức tạp.
Ngoài ra, điều đáng nói là DSU có hợp nhất theo kích thước / hạng, nhưng không nén đường hoạt động trong thời gian $O(\log n)$ cho mỗi truy vấn.
Liên kết theo chỉ số / liên kết tung đồng xu (Linking by index / coin-flip linking)¶
Cả hợp nhất theo hạng và hợp nhất theo kích thước đều yêu cầu bạn lưu trữ thêm dữ liệu cho mỗi tập hợp, và duy trì các giá trị này trong mỗi thao tác hợp nhất. Cũng tồn tại một thuật toán ngẫu nhiên, giúp đơn giản hóa thao tác hợp nhất một chút: liên kết theo chỉ số.
Chúng ta gán cho mỗi tập hợp một giá trị ngẫu nhiên được gọi là chỉ số, và chúng ta gắn tập hợp có chỉ số nhỏ hơn vào tập hợp có chỉ số lớn hơn. Có khả năng là một tập hợp lớn hơn sẽ có chỉ số lớn hơn tập hợp nhỏ hơn, do đó thao tác này liên quan chặt chẽ đến hợp nhất theo kích thước. Trên thực tế, có thể chứng minh rằng, hoạt động này có cùng độ phức tạp thời gian với hợp nhất theo kích thước. Tuy nhiên trong thực tế, nó chậm hơn một chút so với hợp nhất theo kích thước.
Bạn có thể tìm thấy bằng chứng về độ phức tạp và thậm chí nhiều kỹ thuật hợp nhất hơn tại đây.
void make_set(int v) {
parent[v] = v;
index[v] = rand();
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (index[a] < index[b])
swap(a, b);
parent[b] = a;
}
}
Một quan niệm sai lầm phổ biến là chỉ cần tung đồng xu, để quyết định tập hợp nào chúng ta gắn vào tập hợp khác, có cùng độ phức tạp. Tuy nhiên đó không phải là sự thật. Bài báo được liên kết ở trên phỏng đoán rằng liên kết tung đồng xu kết hợp với nén đường có độ phức tạp $\Omega\left(n \frac{\log n}{\log \log n}\right)$. Và trong các điểm chuẩn, nó hoạt động tồi tệ hơn nhiều so với hợp nhất theo kích thước/hạng hoặc liên kết theo chỉ số.
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (rand() % 2)
swap(a, b);
parent[b] = a;
}
}
Ứng dụng và các cải tiến khác (Applications and various improvements)¶
Trong phần này chúng ta xem xét một số ứng dụng của cấu trúc dữ liệu, cả những công dụng tầm thường và một số cải tiến cho cấu trúc dữ liệu.
Thành phần liên thông trong đồ thị (Connected components in a graph)¶
Đây là một trong những ứng dụng rõ ràng của DSU.
Một cách chính thức, bài toán được định nghĩa theo cách sau: Ban đầu chúng ta có một đồ thị rỗng. Chúng ta phải thêm các đỉnh và các cạnh vô hướng, và trả lời các truy vấn có dạng $(a, b)$ - "các đỉnh $a$ và $b$ có nằm trong cùng một thành phần liên thông của đồ thị không?"
Ở đây chúng ta có thể áp dụng trực tiếp cấu trúc dữ liệu này, và nhận được một giải pháp xử lý việc thêm một đỉnh hoặc một cạnh và một truy vấn trong thời gian trung bình gần như hằng số.
Ứng dụng này khá quan trọng, bởi vì bài toán gần như tương tự xuất hiện trong Thuật toán Kruskal để tìm cây khung nhỏ nhất. Sử dụng DSU, chúng ta có thể cải thiện độ phức tạp $O(m \log n + n^2)$ thành $O(m \log n)$.
Tìm kiếm các thành phần liên thông trong ảnh (Search for connected components in an image)¶
Một trong những ứng dụng của DSU là nhiệm vụ sau: có một hình ảnh $n \times m$ pixel. Ban đầu tất cả đều màu trắng, nhưng sau đó một vài pixel màu đen được vẽ. Bạn muốn xác định kích thước của mỗi thành phần liên thông màu trắng trong hình ảnh cuối cùng.
Đối với giải pháp, chúng ta chỉ cần lặp qua tất cả các pixel màu trắng trong hình ảnh, đối với mỗi ô lặp qua bốn hàng xóm của nó, và nếu hàng xóm là màu trắng thì gọi union_sets.
Do đó chúng ta sẽ có một DSU với $n m$ nút tương ứng với các pixel hình ảnh.
Các cây kết quả trong DSU là các thành phần liên thông mong muốn.
Bài toán cũng có thể được giải quyết bằng DFS hoặc BFS, nhưng phương pháp được mô tả ở đây có một lợi thế: nó có thể xử lý ma trận theo từng hàng (tức là để xử lý một hàng chúng ta chỉ cần hàng trước đó và hàng hiện tại, và chỉ cần một DSU được xây dựng cho các phần tử của một hàng) trong bộ nhớ $O(\min(n, m))$.
Lưu trữ thêm thông tin cho mỗi tập hợp (Store additional information for each set)¶
DSU cho phép bạn dễ dàng lưu trữ thêm thông tin trong các tập hợp.
Một ví dụ đơn giản là kích thước của các tập hợp: việc lưu trữ kích thước đã được mô tả trong phần Hợp nhất theo kích thước (thông tin được lưu trữ bởi đại diện hiện tại của tập hợp).
Theo cùng một cách - bằng cách lưu trữ nó tại các nút đại diện - bạn cũng có thể lưu trữ bất kỳ thông tin nào khác về các tập hợp.
Nén các bước nhảy dọc theo đoạn / Tô màu các mảng con offline (Compress jumps along a segment / Painting subarrays offline)¶
Một ứng dụng phổ biến của DSU là như sau: Có một tập hợp các đỉnh, và mỗi đỉnh có một cạnh đi ra đến một đỉnh khác. Với DSU bạn có thể tìm điểm cuối, mà chúng ta đến được sau khi đi theo tất cả các cạnh từ một điểm bắt đầu nhất định, trong thời gian gần như hằng số.
Một ví dụ điển hình của ứng dụng này là bài toán tô màu các mảng con. Chúng ta có một đoạn có độ dài $L$, mỗi phần tử ban đầu có màu 0. Chúng ta phải tô lại mảng con $[l, r]$ với màu $c$ cho mỗi truy vấn $(l, r, c)$. Cuối cùng chúng ta muốn tìm màu cuối cùng của mỗi ô. Chúng ta giả sử rằng chúng ta biết trước tất cả các truy vấn, tức là nhiệm vụ là offline.
Đối với giải pháp, chúng ta có thể tạo một DSU, trong đó mỗi ô lưu trữ một liên kết đến ô chưa được tô tiếp theo. Do đó ban đầu mỗi ô trỏ đến chính nó. Sau khi tô một lần tô lại được yêu cầu của một đoạn, tất cả các ô từ đoạn đó sẽ trỏ đến ô sau đoạn đó.
Bây giờ để giải quyết vấn đề này, chúng ta xem xét các truy vấn theo thứ tự ngược lại: từ cuối cùng đến đầu tiên. Bằng cách này khi chúng ta thực hiện một truy vấn, chúng ta chỉ phải tô chính xác các ô chưa được tô trong mảng con $[l, r]$. Tất cả các ô khác đã chứa màu cuối cùng của chúng. Để lặp nhanh qua tất cả các ô chưa được tô, chúng ta sử dụng DSU. Chúng ta tìm ô chưa được tô ngoài cùng bên trái bên trong một đoạn, tô lại nó, và với con trỏ chúng ta di chuyển đến ô trống tiếp theo bên phải.
Ở đây chúng ta có thể sử dụng DSU với nén đường, nhưng chúng ta không thể sử dụng hợp nhất theo hạng / kích thước (vì điều quan trọng là ai trở thành lãnh đạo sau khi hợp nhất). Do đó độ phức tạp sẽ là $O(\log n)$ cho mỗi lần hợp nhất (cũng khá nhanh).
Cài đặt:
for (int i = 0; i <= L; i++) {
make_set(i);
}
for (int i = m-1; i >= 0; i--) {
int l = query[i].l;
int r = query[i].r;
int c = query[i].c;
for (int v = find_set(l); v <= r; v = find_set(v)) {
answer[v] = c;
parent[v] = v + 1;
}
}
Có một sự tối ưu hóa:
Chúng ta có thể sử dụng hợp nhất theo hạng / kích thước, nếu chúng ta lưu trữ ô chưa được tô tiếp theo trong một mảng bổ sung end[].
Sau đó chúng ta có thể hợp nhất hai tập hợp thành một theo heuristic của chúng, và chúng ta có được giải pháp trong $O(\alpha(n))$.
Hỗ trợ khoảng cách đến đại diện (Support distances up to representative)¶
Đôi khi trong các ứng dụng cụ thể của DSU, bạn cần duy trì khoảng cách giữa một đỉnh và đại diện của tập hợp của nó (tức là độ dài đường đi trong cây từ nút hiện tại đến gốc của cây).
Nếu chúng ta không sử dụng nén đường, khoảng cách chỉ là số lượng các cuộc gọi đệ quy. Nhưng điều này sẽ không hiệu quả.
Tuy nhiên, có thể thực hiện nén đường, nếu chúng ta lưu trữ khoảng cách đến cha như thông tin bổ sung cho mỗi nút.
Trong việc cài đặt, thuận tiện khi sử dụng một mảng các cặp cho parent[] và hàm find_set bây giờ trả về hai số: đại diện của tập hợp và khoảng cách đến nó.
void make_set(int v) {
parent[v] = make_pair(v, 0);
rank[v] = 0;
}
pair<int, int> find_set(int v) {
if (v != parent[v].first) {
int len = parent[v].second;
parent[v] = find_set(parent[v].first);
parent[v].second += len;
}
return parent[v];
}
void union_sets(int a, int b) {
a = find_set(a).first;
b = find_set(b).first;
if (a != b) {
if (rank[a] < rank[b])
swap(a, b);
parent[b] = make_pair(a, 1);
if (rank[a] == rank[b])
rank[a]++;
}
}
Hỗ trợ tính chẵn lẻ của độ dài đường đi / Kiểm tra tính hai phía online (Support the parity of the path length / Checking bipartiteness online)¶
Theo cùng một cách như tính toán độ dài đường đi đến lãnh đạo, có thể duy trì tính chẵn lẻ của độ dài đường đi trước anh ta. Tại sao ứng dụng này nằm trong một đoạn riêng biệt?
Yêu cầu bất thường về việc lưu trữ tính chẵn lẻ của đường đi xuất hiện trong nhiệm vụ sau: ban đầu chúng ta được cho một đồ thị rỗng, nó có thể được thêm các cạnh, và chúng ta phải trả lời các truy vấn có dạng "thành phần liên thông chứa đỉnh này có phải là hai phía không?".
Để giải quyết vấn đề này, chúng ta tạo một DSU để lưu trữ các thành phần và lưu trữ tính chẵn lẻ của đường đi đến đại diện cho mỗi đỉnh. Do đó chúng ta có thể nhanh chóng kiểm tra xem việc thêm một cạnh có dẫn đến vi phạm tính hai phía hay không: cụ thể là nếu các đầu mút của cạnh nằm trong cùng một thành phần liên thông và có cùng độ dài chẵn lẻ đến lãnh đạo, thì việc thêm cạnh này sẽ tạo ra một chu trình có độ dài lẻ, và thành phần sẽ mất tính chất hai phía.
Khó khăn duy nhất mà chúng ta gặp phải là tính toán tính chẵn lẻ trong phương thức union_find.
Nếu chúng ta thêm một cạnh $(a, b)$ kết nối hai thành phần liên thông thành một, thì khi bạn gắn một cây vào cây khác, chúng ta cần điều chỉnh tính chẵn lẻ.
Hãy suy ra một công thức, tính toán tính chẵn lẻ được cấp cho lãnh đạo của tập hợp sẽ được gắn vào tập hợp khác. Gọi $x$ là tính chẵn lẻ của độ dài đường đi từ đỉnh $a$ đến lãnh đạo $A$ của nó, và $y$ là tính chẵn lẻ của độ dài đường đi từ đỉnh $b$ đến lãnh đạo $B$ của nó, và $t$ là tính chẵn lẻ mong muốn mà chúng ta phải gán cho $B$ sau khi hợp nhất. Đường đi bao gồm ba phần: từ $B$ đến $b$, từ $b$ đến $a$, được nối bởi một cạnh và do đó có tính chẵn lẻ $1$, và từ $a$ đến $A$. Do đó chúng ta nhận được công thức ($\oplus$ biểu thị phép toán XOR):
Do đó bất kể chúng ta thực hiện bao nhiêu lần nối, tính chẵn lẻ của các cạnh được mang từ lãnh đạo này sang lãnh đạo khác.
Chúng tôi đưa ra việc cài đặt DSU hỗ trợ tính chẵn lẻ. Như trong phần trước, chúng tôi sử dụng một cặp để lưu trữ tổ tiên và tính chẵn lẻ. Ngoài ra đối với mỗi tập hợp, chúng tôi lưu trữ trong mảng bipartite[] xem nó có còn là hai phía hay không.
void make_set(int v) {
parent[v] = make_pair(v, 0);
rank[v] = 0;
bipartite[v] = true;
}
pair<int, int> find_set(int v) {
if (v != parent[v].first) {
int parity = parent[v].second;
parent[v] = find_set(parent[v].first);
parent[v].second ^= parity;
}
return parent[v];
}
void add_edge(int a, int b) {
pair<int, int> pa = find_set(a);
a = pa.first;
int x = pa.second;
pair<int, int> pb = find_set(b);
b = pb.first;
int y = pb.second;
if (a == b) {
if (x == y)
bipartite[a] = false;
} else {
if (rank[a] < rank[b])
swap (a, b);
parent[b] = make_pair(a, x^y^1);
bipartite[a] &= bipartite[b];
if (rank[a] == rank[b])
++rank[a];
}
}
bool is_bipartite(int v) {
return bipartite[find_set(v).first];
}
RMQ offline (truy vấn phạm vi tối thiểu) trong trung bình $O(\alpha(n))$ / Thủ thuật của Arpa (Offline RMQ (range minimum query) in $O(\alpha(n))$ on average / Arpa's trick)¶
Chúng ta được cho một mảng a[] và chúng ta phải tính toán một số cực tiểu trong các đoạn nhất định của mảng.
Ý tưởng để giải quyết vấn đề này với DSU như sau:
Chúng ta sẽ lặp qua mảng và khi chúng ta ở phần tử thứ i, chúng ta sẽ trả lời tất cả các truy vấn (L, R) với R == i.
Để làm điều này một cách hiệu quả, chúng ta sẽ giữ một DSU bằng cách sử dụng i phần tử đầu tiên với cấu trúc sau: cha của một phần tử là phần tử nhỏ hơn tiếp theo ở bên phải của nó.
Sau đó sử dụng cấu trúc này, câu trả lời cho một truy vấn sẽ là a[find_set(L)], số nhỏ nhất ở bên phải của L.
Cách tiếp cận này rõ ràng chỉ hoạt động offline, tức là nếu chúng ta biết trước tất cả các truy vấn.
Dễ thấy rằng chúng ta có thể áp dụng nén đường. Và chúng ta cũng có thể sử dụng Hợp nhất theo hạng, nếu chúng ta lưu trữ lãnh đạo thực tế trong một mảng riêng biệt.
struct Query {
int L, R, idx;
};
vector<int> answer;
vector<vector<Query>> container;
container[i] chứa tất cả các truy vấn với R == i.
stack<int> s;
for (int i = 0; i < n; i++) {
while (!s.empty() && a[s.top()] > a[i]) {
parent[s.top()] = i;
s.pop();
}
s.push(i);
for (Query q : container[i]) {
answer[q.idx] = a[find_set(q.L)];
}
}
Ngày nay thuật toán này được gọi là thủ thuật của Arpa. Nó được đặt tên theo AmirReza Poorakhavan, người đã độc lập phát hiện và phổ biến kỹ thuật này. Mặc dù thuật toán này đã tồn tại trước khi anh ấy phát hiện ra.
LCA offline (tổ tiên chung thấp nhất trong cây) trong trung bình $O(\alpha(n))$ (Offline LCA (lowest common ancestor in a tree) in $O(\alpha(n))$ on average)¶
Thuật toán để tìm LCA được thảo luận trong bài viết Tổ tiên chung thấp nhất - Thuật toán offline của Tarjan. Thuật toán này so sánh thuận lợi với các thuật toán khác để tìm LCA do sự đơn giản của nó (đặc biệt là so với một thuật toán tối ưu như thuật toán từ Farach-Colton và Bender).
Lưu trữ DSU rõ ràng trong danh sách tập hợp / Ứng dụng của ý tưởng này khi hợp nhất các cấu trúc dữ liệu khác nhau (Storing the DSU explicitly in a set list / Applications of this idea when merging various data structures)¶
Một trong những cách thay thế để lưu trữ DSU là bảo tồn mỗi tập hợp dưới dạng một danh sách các phần tử được lưu trữ rõ ràng. Đồng thời mỗi phần tử cũng lưu trữ tham chiếu đến đại diện của tập hợp của nó.
Thoạt nhìn, điều này trông giống như một cấu trúc dữ liệu không hiệu quả: bằng cách kết hợp hai tập hợp, chúng ta sẽ phải thêm một danh sách vào cuối danh sách khác và phải cập nhật quyền lãnh đạo trong tất cả các phần tử của một trong các danh sách.
Tuy nhiên hóa ra, việc sử dụng heuristic trọng số (tương tự như Hợp nhất theo kích thước) có thể làm giảm đáng kể độ phức tạp tiệm cận: $O(m + n \log n)$ để thực hiện $m$ truy vấn trên $n$ phần tử.
Dưới heuristic trọng số, chúng tôi muốn nói rằng, chúng tôi sẽ luôn thêm tập hợp nhỏ hơn trong hai tập hợp vào tập hợp lớn hơn.
Việc thêm một tập hợp vào tập hợp khác rất dễ thực hiện trong union_sets và sẽ mất thời gian tỷ lệ thuận với kích thước của tập hợp được thêm vào.
Và việc tìm kiếm lãnh đạo trong find_set sẽ mất $O(1)$ với phương pháp lưu trữ này.
Hãy chứng minh độ phức tạp thời gian $O(m + n \log n)$ cho việc thực hiện $m$ truy vấn.
Chúng ta sẽ cố định một phần tử $x$ tùy ý và đếm xem nó được chạm bao nhiêu lần trong thao tác hợp nhất union_sets.
Khi phần tử $x$ được chạm lần đầu tiên, kích thước của tập hợp mới sẽ ít nhất là $2$.
Khi nó được chạm lần thứ hai, tập hợp kết quả sẽ có kích thước ít nhất là $4$, bởi vì tập hợp nhỏ hơn được thêm vào tập hợp lớn hơn.
Và cứ thế tiếp tục.
Điều này có nghĩa là, $x$ chỉ có thể được di chuyển trong tối đa $\log n$ thao tác hợp nhất.
Do đó tổng trên tất cả các đỉnh cho $O(n \log n)$ cộng với $O(1)$ cho mỗi yêu cầu.
Dưới đây là một cài đặt:
vector<int> lst[MAXN];
int parent[MAXN];
void make_set(int v) {
lst[v] = vector<int>(1, v);
parent[v] = v;
}
int find_set(int v) {
return parent[v];
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (lst[a].size() < lst[b].size())
swap(a, b);
while (!lst[b].empty()) {
int v = lst[b].back();
lst[b].pop_back();
parent[v] = a;
lst[a].push_back (v);
}
}
}
Ý tưởng thêm phần nhỏ hơn vào phần lớn hơn này cũng có thể được sử dụng trong rất nhiều giải pháp không liên quan gì đến DSU.
Ví dụ xem xét bài toán sau: chúng ta được cho một cây, mỗi lá có một số được chỉ định (cùng một số có thể xuất hiện nhiều lần trên các lá khác nhau). Chúng ta muốn tính toán số lượng các số khác nhau trong cây con cho mỗi nút của cây.
Áp dụng cho nhiệm vụ này cùng một ý tưởng, có thể có được giải pháp này: chúng ta có thể thực hiện một DFS, sẽ trả về một con trỏ đến một tập hợp các số nguyên - danh sách các số trong cây con đó. Sau đó để nhận câu trả lời cho nút hiện tại (trừ khi tất nhiên nó là một lá), chúng ta gọi DFS cho tất cả các con của nút đó, và hợp nhất tất cả các tập hợp đã nhận lại với nhau. Kích thước của tập hợp kết quả sẽ là câu trả lời cho nút hiện tại. Để kết hợp hiệu quả nhiều tập hợp, chúng ta chỉ cần áp dụng công thức được mô tả ở trên: chúng ta hợp nhất các tập hợp bằng cách đơn giản là thêm các tập hợp nhỏ hơn vào lớn hơn. Cuối cùng chúng ta nhận được một giải pháp $O(n \log^2 n)$, bởi vì một số sẽ chỉ được thêm vào một tập hợp tối đa $O(\log n)$ lần.
Lưu trữ DSU bằng cách duy trì cấu trúc cây rõ ràng / Tìm cầu online trong trung bình $O(\alpha(n))$ (Storing the DSU by maintaining a clear tree structure / Online bridge finding in $O(\alpha(n))$ on average)¶
Một trong những ứng dụng mạnh mẽ nhất của DSU là nó cho phép bạn lưu trữ cả dưới dạng cây nén và không nén. Dạng nén có thể được sử dụng để hợp nhất các cây và để xác minh xem hai đỉnh có nằm trong cùng một cây hay không, và dạng không nén có thể được sử dụng - ví dụ - để tìm kiếm đường đi giữa hai đỉnh nhất định, hoặc các duyệt cây khác.
Trong việc cài đặt, điều này có nghĩa là ngoài mảng tổ tiên nén parent[], chúng ta sẽ cần giữ mảng các tổ tiên không nén real_parent[].
Thật tầm thường khi duy trì mảng bổ sung này sẽ không làm xấu đi độ phức tạp:
các thay đổi trong nó chỉ xảy ra khi chúng ta hợp nhất hai cây, và chỉ trong một phần tử.
Mặt khác khi áp dụng trong thực tế, chúng ta thường cần kết nối các cây bằng cách sử dụng một cạnh được chỉ định khác với việc sử dụng hai nút gốc. Điều này có nghĩa là chúng ta không có lựa chọn nào khác ngoài việc định lại gốc cho một trong các cây (làm cho các đầu mút của cạnh trở thành gốc mới của cây).
Thoạt nhìn có vẻ như việc định lại gốc này rất tốn kém và sẽ làm xấu đi đáng kể độ phức tạp thời gian.
Thật vậy, để định lại gốc một cây tại đỉnh $v$, chúng ta phải đi từ đỉnh đến gốc cũ và thay đổi hướng trong parent[] và real_parent[] cho tất cả các nút trên đường đi đó.
Tuy nhiên trong thực tế nó không tệ đến thế, chúng ta chỉ có thể định lại gốc cây nhỏ hơn trong hai cây tương tự như các ý tưởng trong các phần trước, và nhận được $O(\log n)$ trung bình.
Chi tiết hơn (bao gồm bằng chứng về độ phức tạp thời gian) có thể được tìm thấy trong bài viết Tìm cầu trực tuyến.
Hồi cứu lịch sử (Historical retrospective)¶
Cấu trúc dữ liệu DSU đã được biết đến từ lâu.
Cách lưu trữ cấu trúc này dưới dạng một khu rừng cây dường như được mô tả lần đầu tiên bởi Galler và Fisher vào năm 1964 (Galler, Fisher, "An Improved Equivalence Algorithm), tuy nhiên phân tích hoàn chỉnh về độ phức tạp thời gian đã được thực hiện muộn hơn nhiều.
Các tối ưu hóa nén đường và Hợp nhất theo hạng đã được phát triển bởi McIlroy và Morris, và độc lập với họ cũng bởi Tritter.
Hopcroft và Ullman đã chỉ ra vào năm 1973 độ phức tạp thời gian $O(\log^\star n)$ (Hopcroft, Ullman "Set-merging algorithms") - ở đây $\log^\star$ là logarit lặp (đây là một hàm tăng trưởng chậm, nhưng vẫn không chậm như hàm Ackermann nghịch đảo).
Lần đầu tiên đánh giá về $O(\alpha(n))$ được hiển thị vào năm 1975 (Tarjan "Efficiency of a Good But Not Linear Set Union Algorithm"). Sau đó vào năm 1985, ông cùng với Leeuwen, đã công bố nhiều phân tích độ phức tạp cho một số heuristic hạng và cách nén đường khác nhau (Tarjan, Leeuwen "Worst-case Analysis of Set Union Algorithms").
Cuối cùng vào năm 1989 Fredman và Sachs đã chứng minh rằng trong mô hình tính toán được áp dụng, bất kỳ thuật toán nào cho bài toán hợp nhất tập hợp rời nhau đều phải hoạt động trong ít nhất thời gian trung bình $O(\alpha(n))$ (Fredman, Saks, "The cell probe complexity of dynamic data structures").