Khoảng cách Manhattan (Manhattan Distance)¶

Định nghĩa (Definition)¶

Đối với các điểm $p$ và $q$ trên một mặt phẳng, chúng ta có thể định nghĩa khoảng cách giữa chúng là tổng các hiệu tuyệt đối giữa các tọa độ $x$ và $y$ của chúng:

$$d(p,q) = |x_p - x_q| + |y_p - y_q|$$

Được định nghĩa theo cách này, khoảng cách tương ứng với cái gọi là Hình học Manhattan (taxicab), trong đó các điểm được coi là các giao lộ trong một thành phố được thiết kế tốt, như Manhattan, nơi bạn chỉ có thể di chuyển trên các đường phố theo chiều ngang hoặc chiều dọc, như trong hình ảnh dưới đây:

Hình ảnh này hiển thị một số đường đi ngắn nhất từ một điểm đen đến điểm kia, tất cả chúng đều có độ dài $12$.

Có một số thủ thuật và thuật toán thú vị có thể được thực hiện với khoảng cách này, và chúng tôi sẽ hiển thị một số trong số chúng ở đây.

Cặp điểm xa nhất trong khoảng cách Manhattan (Farthest pair of points in Manhattan distance)¶

Cho $n$ điểm $P$, chúng ta muốn tìm cặp điểm $p,q$ cách xa nhau nhất, nghĩa là tối đa hóa $|x_p - x_q| + |y_p - y_q|$.

Trước tiên hãy suy nghĩ trong một chiều, để $y=0$. Quan sát chính là chúng ta có thể vét cạn xem $|x_p - x_q|$ bằng $x_p - x_q$ hay $-x_p + x_q$, bởi vì nếu chúng ta "nhầm dấu" của giá trị tuyệt đối, chúng ta sẽ chỉ nhận được giá trị nhỏ hơn, vì vậy nó không thể ảnh hưởng đến câu trả lời. Một cách chính thức hơn, điều sau đây đúng:

$$|x_p - x_q| = \max(x_p - x_q, -x_p + x_q)$$

Vì vậy, ví dụ, chúng ta có thể cố gắng có $p$ sao cho $x_p$ có dấu cộng, và sau đó $q$ phải có dấu trừ. Bằng cách này, chúng ta muốn tìm:

$$\max\limits_{p, q \in P}(x_p + (-x_q)) = \max\limits_{p \in P}(x_p) + \max\limits_{q \in P}( - x_q ).$$

Lưu ý rằng chúng ta có thể mở rộng ý tưởng này thêm cho 2 (hoặc nhiều hơn!) chiều. Đối với $d$ chiều, chúng ta phải vét cạn $2^d$ giá trị có thể của các dấu. Ví dụ, nếu chúng ta ở trong $2$ chiều và vét cạn rằng $p$ có cả hai dấu cộng, chúng ta muốn tìm:

$$\max\limits_{p, q \in P} [(x_p + (-x_q)) + (y_p + (-y_q))] = \max\limits_{p \in P}(x_p + y_p) + \max\limits_{q \in P}(-x_q - y_q).$$

Vì chúng ta đã làm cho $p$ và $q$ độc lập, bây giờ thật dễ dàng để tìm $p$ và $q$ tối đa hóa biểu thức.

Mã dưới đây tổng quát hóa điều này cho $d$ chiều và chạy trong $O(n \cdot 2^d \cdot d)$.

long long ans = 0;
for (int msk = 0; msk < (1 << d); msk++) {
    long long mx = LLONG_MIN, mn = LLONG_MAX;
    for (int i = 0; i < n; i++) {
        long long cur = 0;
        for (int j = 0; j < d; j++) {
            if (msk & (1 << j)) cur += p[i][j];
            else cur -= p[i][j];
        }
        mx = max(mx, cur);
        mn = min(mn, cur);
    }
    ans = max(ans, mx - mn);
}

Xoay các điểm và khoảng cách Chebyshev (Rotating the points and Chebyshev distance)¶

Đã biết rằng, đối với mọi $m, n \in \mathbb{R}$,

$$|m| + |n| = \text{max}(|m + n|, |m - n|).$$

Để chứng minh điều này, chúng ta chỉ cần phân tích dấu của $m$ và $n$. Và nó được để lại như một bài tập.

Chúng ta có thể áp dụng phương trình này cho công thức khoảng cách Manhattan để tìm ra rằng

$$d((x_1, y_1), (x_2, y_2)) = |x_1 - x_2| + |y_1 - y_2| = \text{max}(|(x_1 + y_1) - (x_2 + y_2)|, |(y_1 - x_1) - (y_2 - x_2)|).$$

Biểu thức cuối cùng trong phương trình trước là khoảng cách Chebyshev của các điểm $(x_1 + y_1, y_1 - x_1)$ và $(x_2 + y_2, y_2 - x_2)$. Điều này có nghĩa là, sau khi áp dụng phép biến đổi

$$\alpha : (x, y) \to (x + y, y - x),$$

khoảng cách Manhattan giữa các điểm $p$ và $q$ biến thành khoảng cách Chebyshev giữa $\alpha(p)$ và $\alpha(q)$.

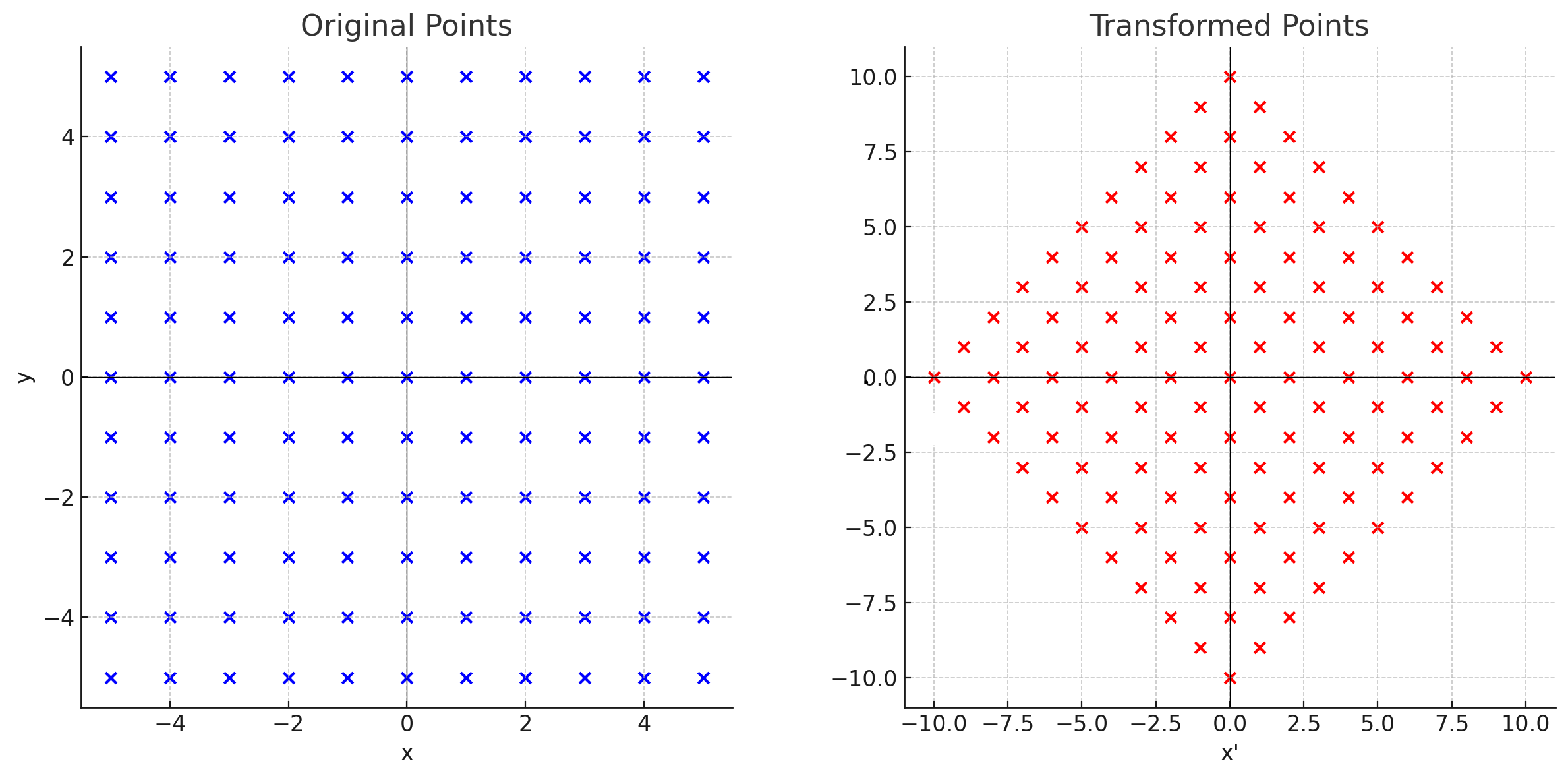
Ngoài ra, chúng ta có thể nhận ra rằng $\alpha$ là một đồng dạng xoắn ốc (spiral similarity) (phép quay mặt phẳng theo sau bởi phép co giãn quanh tâm $O$) với tâm $(0, 0)$, góc quay $45^{\circ}$ theo chiều kim đồng hồ và phép co giãn bởi $\sqrt{2}$.

Dưới đây là một hình ảnh để giúp hình dung phép biến đổi:

Cây khung nhỏ nhất Manhattan (Manhattan Minimum Spanning Tree)¶

Bài toán MST Manhattan bao gồm, cho một số điểm trong mặt phẳng, tìm các cạnh kết nối tất cả các điểm và có tổng trọng số tối thiểu. Trọng số của một cạnh nối hai điểm là khoảng cách Manhattan của chúng. Để đơn giản, chúng ta giả sử rằng tất cả các điểm có vị trí khác nhau. Ở đây chúng tôi chỉ ra một cách tìm MST trong $O(n \log{n})$ bằng cách tìm cho mỗi điểm người hàng xóm gần nhất của nó trong mỗi góc một phần tám (octant), được biểu diễn bởi hình ảnh bên dưới. Điều này sẽ cho chúng ta $O(n)$ cạnh ứng viên, mà như chúng tôi chỉ ra bên dưới, sẽ đảm bảo rằng chúng chứa MST. Bước cuối cùng sau đó là sử dụng một thuật toán MST tiêu chuẩn nào đó, ví dụ, thuật toán Kruskal sử dụng Disjoint Set Union.

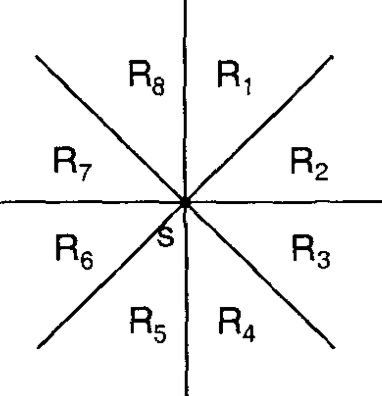*8 octant so với điểm S*

Thuật toán được trình bày ở đây lần đầu tiên được trình bày trong một bài báo từ H. Zhou, N. Shenoy, và W. Nichollos (2002). Cũng có một thuật toán khác được biết đến sử dụng cách tiếp cận Chia để trị bởi J. Stolfi, cũng rất thú vị và chỉ khác nhau ở cách chúng tìm người hàng xóm gần nhất trong mỗi octant. Cả hai đều có cùng độ phức tạp, nhưng cái được trình bày ở đây dễ cài đặt hơn và có hằng số nhỏ hơn.

Đầu tiên, hãy hiểu tại sao chỉ cần xem xét người hàng xóm gần nhất trong mỗi octant là đủ. Ý tưởng là chỉ ra rằng đối với một điểm $s$ và bất kỳ hai điểm nào khác $p$ và $q$ trong cùng một octant, $d(p, q) < \max(d(s, p), d(s, q))$. Điều này rất quan trọng, vì nó cho thấy rằng nếu có một MST trong đó $s$ được kết nối với cả $p$ và $q$, chúng ta có thể xóa một trong những cạnh này và thêm cạnh $(p,q)$, điều này sẽ làm giảm tổng chi phí. Để chứng minh điều này, chúng ta giả sử không mất tính tổng quát rằng $p$ và $q$ nằm trong octant $R_1$, được định nghĩa bởi: $x_s \leq x$ và $x_s - y_s > x - y$, và sau đó thực hiện một số trường hợp. Hình ảnh dưới đây đưa ra một số trực giác về lý do tại sao điều này đúng.

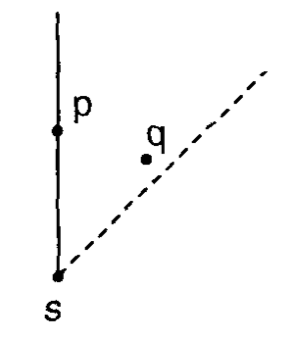*Về mặt trực giác, giới hạn của octant làm cho không thể có chuyện $p$ và $q$ đều gần $s$ hơn là gần nhau*

Do đó, câu hỏi chính là làm thế nào để tìm người hàng xóm gần nhất trong mỗi octant cho mỗi điểm trong số $n$ điểm.

Người hàng xóm gần nhất trong mỗi Octant trong O(n log n) (Nearest Neighbor in each Octant in O(n log n))¶

Để đơn giản, chúng tôi tập trung vào octant NNE (Bắc-Đông Bắc) ($R_1$ trong hình trên). Tất cả các hướng khác có thể được tìm thấy bằng cùng một thuật toán bằng cách quay đầu vào.

Chúng tôi sẽ sử dụng phương pháp quét đường (sweep-line). Chúng tôi xử lý các điểm từ tây-nam đến đông-bắc, tức là, theo thứ tự $x + y$ không giảm. Chúng tôi cũng giữ một tập hợp các điểm chưa có người hàng xóm gần nhất của chúng, mà chúng tôi gọi là "tập hợp hoạt động". Chúng tôi thêm các hình ảnh dưới đây để giúp hình dung thuật toán.

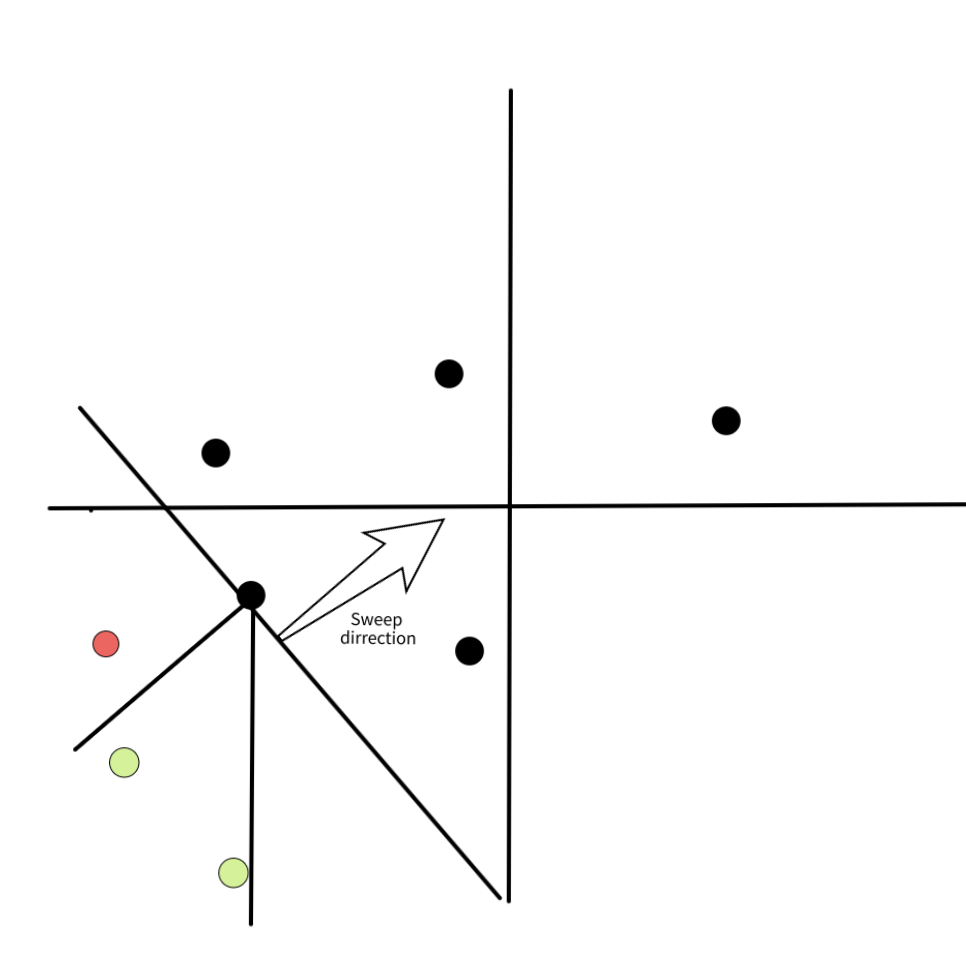*Màu đen có mũi tên bạn có thể thấy hướng của việc quét đường. Tất cả các điểm bên dưới đường này nằm trong tập hợp hoạt động, và các điểm bên trên vẫn chưa được xử lý. Màu xanh lá cây chúng ta thấy các điểm nằm trong octant của điểm được xử lý. Màu đỏ là các điểm không nằm trong octant được tìm kiếm.*

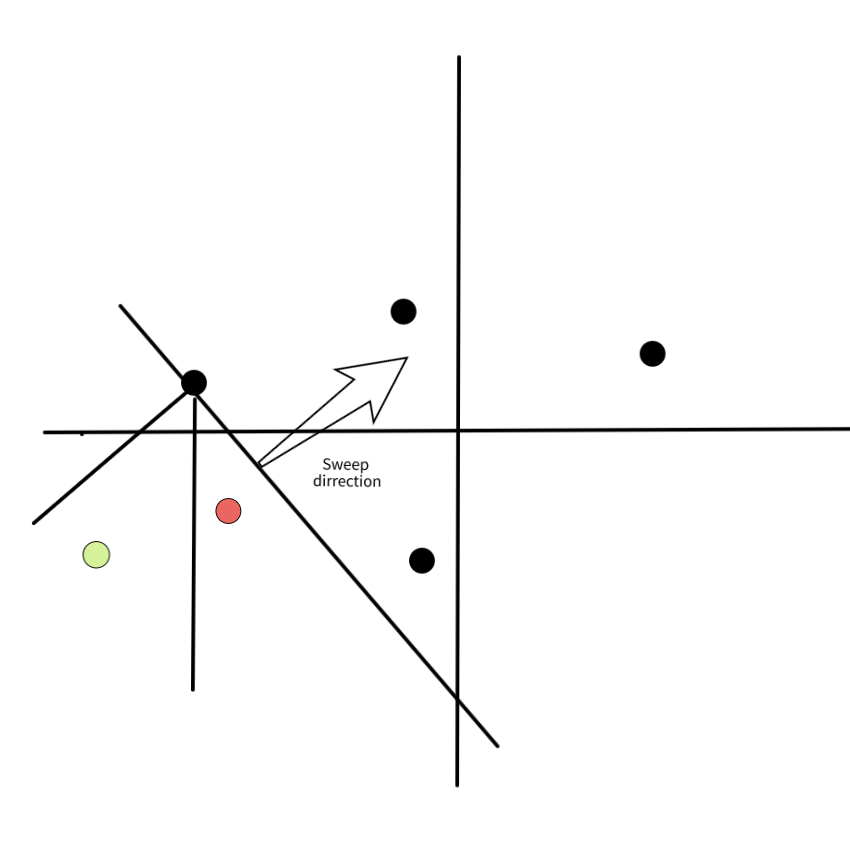*Trong hình ảnh này, chúng ta thấy tập hợp hoạt động sau khi xử lý điểm $p$. Lưu ý rằng $2$ điểm màu xanh lá cây của hình ảnh trước đó có $p$ ở octant bắc-đông-bắc của nó và không còn trong tập hợp hoạt động nữa, bởi vì chúng đã tìm thấy người hàng xóm gần nhất của chúng.*

Khi chúng ta thêm một điểm mới $p$, đối với mọi điểm $s$ có nó trong octant của nó, chúng ta có thể gán $p$ làm người hàng xóm gần nhất một cách an toàn. Điều này đúng vì khoảng cách của chúng là $d(p,s) = |x_p - x_s| + |y_p - y_s| = (x_p + y_p) - (x_s + y_s)$, bởi vì $p$ nằm trong octant bắc-đông-bắc. Vì tất cả các điểm tiếp theo sẽ không có giá trị $x + y$ nhỏ hơn do bước sắp xếp, $p$ được đảm bảo có khoảng cách nhỏ hơn. Sau đó chúng ta có thể xóa tất cả các điểm như vậy khỏi tập hợp hoạt động, và cuối cùng thêm $p$ vào tập hợp hoạt động.

Câu hỏi tiếp theo là làm thế nào để tìm một cách hiệu quả những điểm $s$ có $p$ trong octant bắc-đông-bắc. Nghĩa là, những điểm $s$ nào thỏa mãn:

$x_s \leq x_p$
$x_p - y_p < x_s - y_s$

Vì không có điểm nào trong tập hợp hoạt động nằm trong vùng $R_1$ của điểm khác, chúng ta cũng có rằng đối với hai điểm $q_1$ và $q_2$ trong tập hợp hoạt động, $x_{q_1} \neq x_{q_2}$ và thứ tự của chúng ngụ ý $x_{q_1} < x_{q_2} \implies x_{q_1} - y_{q_1} \leq x_{q_2} - y_{q_2}$.

Bạn có thể cố gắng hình dung điều này trên các hình ảnh trên bằng cách nghĩ về thứ tự của $x - y$ như một "đường quét" đi từ tây-bắc đến đông-nam, tức là vuông góc với đường được vẽ.

Điều này có nghĩa là nếu chúng ta giữ tập hợp hoạt động được sắp xếp theo $x$, các ứng viên $s$ được đặt liên tiếp nhau. Sau đó chúng ta có thể tìm $x_s \leq x_p$ lớn nhất và xử lý các điểm theo thứ tự giảm dần của $x$ cho đến khi điều kiện thứ hai $x_p - y_p < x_s - y_s$ bị phá vỡ (chúng ta thực sự có thể cho phép $x_p - y_p = x_s - y_s$ và điều đó giải quyết trường hợp các điểm có tọa độ bằng nhau). Lưu ý rằng vì chúng ta xóa khỏi tập hợp ngay sau khi xử lý, điều này sẽ có độ phức tạp khấu hao là $O(n \log(n))$. Bây giờ chúng ta có điểm gần nhất theo hướng đông-bắc, chúng ta xoay các điểm và lặp lại. Có thể chỉ ra rằng thực tế chúng ta cũng tìm thấy theo cách này điểm gần nhất theo hướng tây-nam, vì vậy chúng ta có thể lặp lại chỉ 4 lần, thay vì 8.

Tóm lại chúng ta:

Sắp xếp các điểm theo $x + y$ theo thứ tự không giảm;
Đối với mọi điểm, chúng ta lặp qua tập hợp hoạt động bắt đầu với điểm có $x$ lớn nhất sao cho $x \leq x_p$, và chúng ta ngắt vòng lặp nếu $x_p - y_p \geq x_s - y_s$. Đối với mọi điểm hợp lệ $s$ chúng ta thêm cạnh $(s,p, d(s,p))$ vào danh sách của chúng ta;
Chúng ta thêm điểm $p$ vào tập hợp hoạt động;
Xoay các điểm và lặp lại cho đến khi chúng ta lặp qua tất cả các octant.
Áp dụng thuật toán Kruskal trên danh sách các cạnh để lấy MST.

Dưới đây bạn có thể tìm thấy một cài đặt, dựa trên một cài đặt từ KACTL.

manhattan_mst

struct point {
    long long x, y;
};

// Returns a list of edges in the format (weight, u, v). 
// Passing this list to Kruskal algorithm will give the Manhattan MST.
vector<tuple<long long, int, int>> manhattan_mst_edges(vector<point> ps) {
    vector<int> ids(ps.size());
    iota(ids.begin(), ids.end(), 0);
    vector<tuple<long long, int, int>> edges;
    for (int rot = 0; rot < 4; rot++) { // for every rotation
        sort(ids.begin(), ids.end(), [&](int i, int j){
            return (ps[i].x + ps[i].y) < (ps[j].x + ps[j].y);
        });
        map<int, int, greater<int>> active; // (xs, id)
        for (auto i : ids) {
            for (auto it = active.lower_bound(ps[i].x); it != active.end();
            active.erase(it++)) {
                int j = it->second;
                if (ps[i].x - ps[i].y > ps[j].x - ps[j].y) break;
                assert(ps[i].x >= ps[j].x && ps[i].y >= ps[j].y);
                edges.push_back({(ps[i].x - ps[j].x) + (ps[i].y - ps[j].y), i, j});
            }
            active[ps[i].x] = i;
        }
        for (auto &p : ps) { // rotate
            if (rot & 1) p.x *= -1;
            else swap(p.x, p.y);
        }
    }
    return edges;
}