Tam giác đạc Delaunay và biểu đồ Voronoi (Delaunay triangulation and Voronoi diagram)¶
Xem xét một tập hợp $\{p_i\}$ các điểm trên mặt phẳng. Một biểu đồ Voronoi (Voronoi diagram) $V(\{p_i\})$ của $\{p_i\}$ là một phân vùng của mặt phẳng thành $n$ vùng $V_i$, trong đó $V_i = \{p\in\mathbb{R}^2;\ \rho(p, p_i) = \min\ \rho(p, p_k)\}$. Các ô (cell) của biểu đồ Voronoi là các đa giác (có thể vô hạn). Một tam giác đạc Delaunay (Delaunay triangulation) $D(\{p_i\})$ của $\{p_i\}$ là một phép đạc tam giác trong đó mọi điểm $p_i$ nằm ngoài hoặc nằm trên biên của đường tròn ngoại tiếp của mỗi tam giác $T \in D(\{p_i\})$.
Có một trường hợp suy biến khó chịu khi biểu đồ Voronoi không liên thông và tam giác đạc Delaunay không tồn tại. Trường hợp này là khi tất cả các điểm đều thẳng hàng.
Tính chất (Properties)¶
Tam giác đạc Delaunay tối đa hóa góc nhỏ nhất trong số tất cả các phép đạc tam giác có thể.
Cây khung Euclide nhỏ nhất (Minimum Euclidean spanning tree) của một tập hợp điểm là một tập hợp con các cạnh của tam giác đạc Delaunay của nó.
Tính đối ngẫu (Duality)¶
Giả sử rằng $\{p_i\}$ không thẳng hàng và trong số $\{p_i\}$ không có bốn điểm nào nằm trên cùng một đường tròn. Khi đó $V(\{p_i\})$ và $D(\{p_i\})$ là đối ngẫu (dual), vì vậy nếu chúng ta có được một trong số chúng, chúng ta có thể có được cái kia trong $O(n)$. Phải làm gì nếu không phải trường hợp đó? Trường hợp thẳng hàng có thể được xử lý dễ dàng. Nếu không, $V$ và $D'$ là đối ngẫu, trong đó $D'$ thu được từ $D$ bằng cách loại bỏ tất cả các cạnh sao cho hai tam giác trên cạnh này chia sẻ đường tròn ngoại tiếp.
Xây dựng Delaunay và Voronoi (Building Delaunay and Voronoi)¶
Do tính đối ngẫu, chúng ta chỉ cần một thuật toán nhanh để tính toán chỉ một trong $V$ và $D$. Chúng ta sẽ mô tả cách xây dựng $D(\{p_i\})$ trong $O(n\log n)$. Phép đạc tam giác sẽ được xây dựng thông qua thuật toán chia để trị (divide-and-conquer) do Guibas và Stolfi đề xuất.
Cấu trúc dữ liệu cạnh tứ giác (Quad-edge data structure)¶
Trong thuật toán, $D$ sẽ được lưu trữ bên trong cấu trúc dữ liệu cạnh tứ giác (quad-edge). Cấu trúc này được mô tả trong hình:
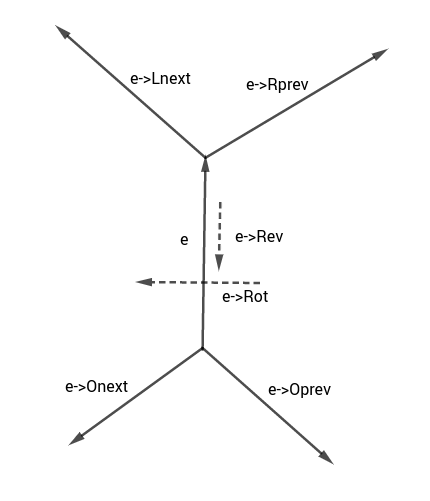
Trong thuật toán, chúng ta sẽ sử dụng các hàm sau trên các cạnh:
make_edge(a, b)
Hàm này tạo ra một cạnh cô lập từ điểmađến điểmbcùng với cạnh ngược của nó và cả hai cạnh đối ngẫu.splice(a, b)
Đây là một hàm chính của thuật toán. Nó hoán đổia->Onextvớib->Onextvàa->Onext->Rot->Onextvớib->Onext->Rot->Onext.delete_edge(e)
Hàm này xóaekhỏi tam giác đạc. Để xóae, chúng ta có thể chỉ cần gọisplice(e, e->Oprev)vàsplice(e->Rev, e->Rev->Oprev).connect(a, b)
Hàm này tạo một cạnh mớietừa->Destđếnb->Orgsao choa,b,eđều có cùng một mặt trái. Để làm điều này, chúng ta gọie = make_edge(a->Dest, b->Org),splice(e, a->Lnext)vàsplice(e->Rev, b).
Thuật toán (Algorithm)¶
Thuật toán sẽ tính toán tam giác đạc và trả về hai cạnh tứ giác: cạnh bao lồi ngược chiều kim đồng hồ ra khỏi đỉnh ngoài cùng bên trái và cạnh bao lồi cùng chiều kim đồng hồ ra khỏi đỉnh ngoài cùng bên phải.
Hãy sắp xếp tất cả các điểm theo x, và nếu $x_1 = x_2$ thì theo y. Hãy giải quyết bài toán cho một đoạn $(l, r)$ nào đó (ban đầu $(l, r) = (0, n - 1)$). Nếu $r - l + 1 = 2$, chúng ta sẽ thêm một cạnh $(p[l], p[r])$ và trả về. Nếu $r - l + 1 = 3$, trước tiên chúng ta sẽ thêm các cạnh $(p[l], p[l + 1])$ và $(p[l + 1], p[r])$. Chúng ta cũng phải kết nối chúng bằng cách sử dụng splice(a->Rev, b). Bây giờ chúng ta phải đóng tam giác. Hành động tiếp theo của chúng ta sẽ phụ thuộc vào hướng của $p[l], p[l + 1], p[r]$. Nếu chúng thẳng hàng, chúng ta không thể tạo một tam giác, vì vậy chúng ta chỉ cần trả về (a, b->Rev). Ngược lại, chúng ta tạo một cạnh mới c bằng cách gọi connect(b, a). Nếu các điểm được định hướng ngược chiều kim đồng hồ, chúng ta trả về (a, b->Rev). Ngược lại, chúng ta trả về (c->Rev, c).
Bây giờ giả sử rằng $r - l + 1 \ge 4$. Đầu tiên, hãy giải $L = (l, \frac{l + r}{2})$ và $R = (\frac{l + r}{2} + 1, r)$ một cách đệ quy. Bây giờ chúng ta phải hợp nhất các tam giác đạc này thành một tam giác đạc. Lưu ý rằng các điểm của chúng ta đã được sắp xếp, vì vậy trong khi hợp nhất, chúng ta sẽ thêm các cạnh từ L đến R (được gọi là các cạnh chéo - cross edges) và loại bỏ một số cạnh từ L đến L và từ R đến R.
Cấu trúc của các cạnh chéo là gì? Tất cả các cạnh này phải cắt một đường thẳng song song với trục y và đặt tại giá trị x phân chia. Điều này thiết lập một thứ tự tuyến tính của các cạnh chéo, vì vậy chúng ta có thể nói về các cạnh chéo liên tiếp, cạnh chéo dưới cùng, v.v. Thuật toán sẽ thêm các cạnh chéo theo thứ tự tăng dần. Lưu ý rằng bất kỳ hai cạnh chéo liền kề nào cũng sẽ có một đầu mút chung, và cạnh thứ ba của tam giác mà chúng xác định đi từ L đến L hoặc từ R đến R. Hãy gọi cạnh chéo hiện tại là cơ sở (base). Người kế vị của cơ sở sẽ đi từ đầu mút bên trái của cơ sở đến một trong các láng giềng R của đầu mút bên phải hoặc ngược lại.
Xem xét đường tròn ngoại tiếp của cơ sở và cạnh chéo trước đó.
Giả sử đường tròn này được chuyển đổi thành các đường tròn khác có cơ sở là dây cung nhưng nằm xa hơn về hướng Oy.
Đường tròn của chúng ta sẽ đi lên một lúc, nhưng trừ khi cơ sở là tiếp tuyến trên của L và R, chúng ta sẽ gặp một điểm thuộc L hoặc R tạo ra một tam giác mới mà không có bất kỳ điểm nào trong đường tròn ngoại tiếp.
Cạnh L-R mới của tam giác này là cạnh chéo tiếp theo được thêm vào.
Để thực hiện điều này một cách hiệu quả, chúng ta tính toán hai cạnh lcand và rcand sao cho lcand trỏ đến điểm L đầu tiên gặp phải trong quá trình này, và rcand trỏ đến điểm R đầu tiên.
Sau đó, chúng ta chọn cái sẽ gặp phải đầu tiên. Ban đầu cơ sở trỏ đến tiếp tuyến dưới của L và R.
Cài đặt (Implementation)¶
Lưu ý rằng việc cài đặt hàm in_circle là đặc thù của GCC.
typedef long long ll;
bool ge(const ll& a, const ll& b) { return a >= b; }
bool le(const ll& a, const ll& b) { return a <= b; }
bool eq(const ll& a, const ll& b) { return a == b; }
bool gt(const ll& a, const ll& b) { return a > b; }
bool lt(const ll& a, const ll& b) { return a < b; }
int sgn(const ll& a) { return a >= 0 ? a ? 1 : 0 : -1; }
struct pt {
ll x, y;
pt() { }
pt(ll _x, ll _y) : x(_x), y(_y) { }
pt operator-(const pt& p) const {
return pt(x - p.x, y - p.y);
}
ll cross(const pt& p) const {
return x * p.y - y * p.x;
}
ll cross(const pt& a, const pt& b) const {
return (a - *this).cross(b - *this);
}
ll dot(const pt& p) const {
return x * p.x + y * p.y;
}
ll dot(const pt& a, const pt& b) const {
return (a - *this).dot(b - *this);
}
ll sqrLength() const {
return this->dot(*this);
}
bool operator==(const pt& p) const {
return eq(x, p.x) && eq(y, p.y);
}
};
const pt inf_pt = pt(1e18, 1e18);
struct QuadEdge {
pt origin;
QuadEdge* rot = nullptr;
QuadEdge* onext = nullptr;
bool used = false;
QuadEdge* rev() const {
return rot->rot;
}
QuadEdge* lnext() const {
return rot->rev()->onext->rot;
}
QuadEdge* oprev() const {
return rot->onext->rot;
}
pt dest() const {
return rev()->origin;
}
};
QuadEdge* make_edge(pt from, pt to) {
QuadEdge* e1 = new QuadEdge;
QuadEdge* e2 = new QuadEdge;
QuadEdge* e3 = new QuadEdge;
QuadEdge* e4 = new QuadEdge;
e1->origin = from;
e2->origin = to;
e3->origin = e4->origin = inf_pt;
e1->rot = e3;
e2->rot = e4;
e3->rot = e2;
e4->rot = e1;
e1->onext = e1;
e2->onext = e2;
e3->onext = e4;
e4->onext = e3;
return e1;
}
void splice(QuadEdge* a, QuadEdge* b) {
swap(a->onext->rot->onext, b->onext->rot->onext);
swap(a->onext, b->onext);
}
void delete_edge(QuadEdge* e) {
splice(e, e->oprev());
splice(e->rev(), e->rev()->oprev());
delete e->rev()->rot;
delete e->rev();
delete e->rot;
delete e;
}
QuadEdge* connect(QuadEdge* a, QuadEdge* b) {
QuadEdge* e = make_edge(a->dest(), b->origin);
splice(e, a->lnext());
splice(e->rev(), b);
return e;
}
bool left_of(pt p, QuadEdge* e) {
return gt(p.cross(e->origin, e->dest()), 0);
}
bool right_of(pt p, QuadEdge* e) {
return lt(p.cross(e->origin, e->dest()), 0);
}
template <class T>
T det3(T a1, T a2, T a3, T b1, T b2, T b3, T c1, T c2, T c3) {
return a1 * (b2 * c3 - c2 * b3) - a2 * (b1 * c3 - c1 * b3) +
a3 * (b1 * c2 - c1 * b2);
}
bool in_circle(pt a, pt b, pt c, pt d) {
// If there is __int128, calculate directly.
// Otherwise, calculate angles.
#if defined(__LP64__) || defined(_WIN64)
__int128 det = -det3<__int128>(b.x, b.y, b.sqrLength(), c.x, c.y,
c.sqrLength(), d.x, d.y, d.sqrLength());
det += det3<__int128>(a.x, a.y, a.sqrLength(), c.x, c.y, c.sqrLength(), d.x,
d.y, d.sqrLength());
det -= det3<__int128>(a.x, a.y, a.sqrLength(), b.x, b.y, b.sqrLength(), d.x,
d.y, d.sqrLength());
det += det3<__int128>(a.x, a.y, a.sqrLength(), b.x, b.y, b.sqrLength(), c.x,
c.y, c.sqrLength());
return det > 0;
#else
auto ang = [](pt l, pt mid, pt r) {
ll x = mid.dot(l, r);
ll y = mid.cross(l, r);
long double res = atan2((long double)x, (long double)y);
return res;
};
long double kek = ang(a, b, c) + ang(c, d, a) - ang(b, c, d) - ang(d, a, b);
if (kek > 1e-8)
return true;
else
return false;
#endif
}
pair<QuadEdge*, QuadEdge*> build_tr(int l, int r, vector<pt>& p) {
if (r - l + 1 == 2) {
QuadEdge* res = make_edge(p[l], p[r]);
return make_pair(res, res->rev());
}
if (r - l + 1 == 3) {
QuadEdge *a = make_edge(p[l], p[l + 1]), *b = make_edge(p[l + 1], p[r]);
splice(a->rev(), b);
int sg = sgn(p[l].cross(p[l + 1], p[r]));
if (sg == 0)
return make_pair(a, b->rev());
QuadEdge* c = connect(b, a);
if (sg == 1)
return make_pair(a, b->rev());
else
return make_pair(c->rev(), c);
}
int mid = (l + r) / 2;
QuadEdge *ldo, *ldi, *rdo, *rdi;
tie(ldo, ldi) = build_tr(l, mid, p);
tie(rdi, rdo) = build_tr(mid + 1, r, p);
while (true) {
if (left_of(rdi->origin, ldi)) {
ldi = ldi->lnext();
continue;
}
if (right_of(ldi->origin, rdi)) {
rdi = rdi->rev()->onext;
continue;
}
break;
}
QuadEdge* basel = connect(rdi->rev(), ldi);
auto valid = [&basel](QuadEdge* e) { return right_of(e->dest(), basel); };
if (ldi->origin == ldo->origin)
ldo = basel->rev();
if (rdi->origin == rdo->origin)
rdo = basel;
while (true) {
QuadEdge* lcand = basel->rev()->onext;
if (valid(lcand)) {
while (in_circle(basel->dest(), basel->origin, lcand->dest(),
lcand->onext->dest())) {
QuadEdge* t = lcand->onext;
delete_edge(lcand);
lcand = t;
}
}
QuadEdge* rcand = basel->oprev();
if (valid(rcand)) {
while (in_circle(basel->dest(), basel->origin, rcand->dest(),
rcand->oprev()->dest())) {
QuadEdge* t = rcand->oprev();
delete_edge(rcand);
rcand = t;
}
}
if (!valid(lcand) && !valid(rcand))
break;
if (!valid(lcand) ||
(valid(rcand) && in_circle(lcand->dest(), lcand->origin,
rcand->origin, rcand->dest())))
basel = connect(rcand, basel->rev());
else
basel = connect(basel->rev(), lcand->rev());
}
return make_pair(ldo, rdo);
}
vector<tuple<pt, pt, pt>> delaunay(vector<pt> p) {
sort(p.begin(), p.end(), [](const pt& a, const pt& b) {
return lt(a.x, b.x) || (eq(a.x, b.x) && lt(a.y, b.y));
});
auto res = build_tr(0, (int)p.size() - 1, p);
QuadEdge* e = res.first;
vector<QuadEdge*> edges = {e};
while (lt(e->onext->dest().cross(e->dest(), e->origin), 0))
e = e->onext;
auto add = [&p, &e, &edges]() {
QuadEdge* curr = e;
do {
curr->used = true;
p.push_back(curr->origin);
edges.push_back(curr->rev());
curr = curr->lnext();
} while (curr != e);
};
add();
p.clear();
int kek = 0;
while (kek < (int)edges.size()) {
if (!(e = edges[kek++])->used)
add();
}
vector<tuple<pt, pt, pt>> ans;
for (int i = 0; i < (int)p.size(); i += 3) {
ans.push_back(make_tuple(p[i], p[i + 1], p[i + 2]));
}
return ans;
}