Tìm kiếm một cặp đoạn thẳng giao nhau (Search for a pair of intersecting segments)¶
Cho $n$ đoạn thẳng trên mặt phẳng. Yêu cầu kiểm tra xem có ít nhất hai trong số chúng cắt nhau hay không. Nếu câu trả lời là có, hãy in ra cặp đoạn thẳng giao nhau này; chỉ cần chọn bất kỳ cặp nào trong số chúng nếu có nhiều câu trả lời.
Thuật toán giải pháp ngây thơ (naive) là lặp qua tất cả các cặp đoạn thẳng trong $O(n^2)$ và kiểm tra từng cặp xem chúng có cắt nhau hay không. Bài viết này mô tả một thuật toán với thời gian chạy $O(n \log n)$, dựa trên thuật toán quét đường (sweep line algorithm).
Thuật toán (Algorithm)¶
Hãy vẽ một đường thẳng đứng $x = -\infty$ trong tâm trí và bắt đầu di chuyển đường này sang phải. Trong quá trình di chuyển của nó, đường này sẽ gặp các đoạn thẳng, và tại mỗi thời điểm một đoạn thẳng cắt đường thẳng của chúng ta, nó cắt nhau tại đúng một điểm (chúng ta sẽ giả sử rằng không có đoạn thẳng đứng nào).
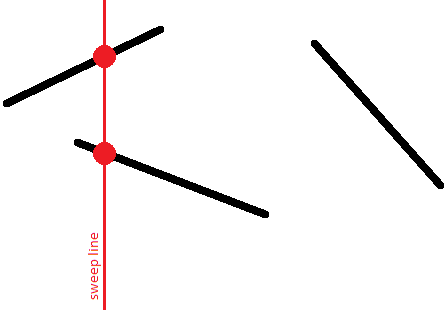
Do đó, đối với mỗi đoạn thẳng, tại một thời điểm nào đó, điểm của nó sẽ xuất hiện trên đường quét, sau đó cùng với chuyển động của đường, điểm này sẽ di chuyển, và cuối cùng, tại một thời điểm nào đó, đoạn thẳng sẽ biến mất khỏi đường quét.
Chúng ta quan tâm đến thứ tự tương đối của các đoạn thẳng dọc theo phương thẳng đứng. Cụ thể, chúng ta sẽ lưu trữ một danh sách các đoạn thẳng cắt đường quét tại một thời điểm nhất định, trong đó các đoạn thẳng sẽ được sắp xếp theo tọa độ $y$ của chúng trên đường quét.
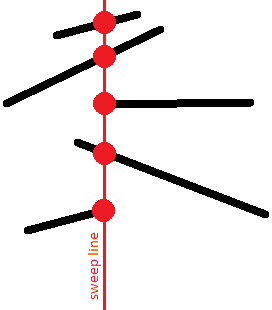
Thứ tự này thú vị bởi vì các đoạn thẳng giao nhau sẽ có cùng tọa độ $y$ ít nhất tại một thời điểm:
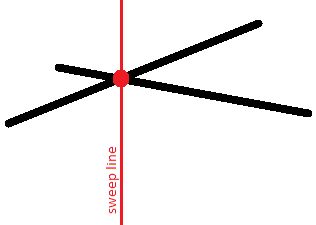
Chúng ta hình thành các tuyên bố chính:
- Để tìm một cặp đoạn thẳng giao nhau, chỉ cần xem xét các đoạn thẳng liền kề tại mỗi vị trí cố định của đường quét là đủ.
- Chỉ cần xem xét đường quét không phải ở tất cả các vị trí thực có thể $(-\infty \ldots +\infty)$, mà chỉ ở những vị trí khi các đoạn thẳng mới xuất hiện hoặc các đoạn thẳng cũ biến mất. Nói cách khác, chỉ cần giới hạn bản thân trong các vị trí bằng với hoành độ (abscissas) của các điểm cuối của các đoạn thẳng.
- Khi một đoạn thẳng mới xuất hiện, chỉ cần chèn nó vào vị trí mong muốn trong danh sách thu được cho đường quét trước đó. Chúng ta chỉ nên kiểm tra sự giao nhau của đoạn thẳng đã thêm với các hàng xóm trực tiếp của nó trong danh sách ở trên và ở dưới.
- Nếu đoạn thẳng biến mất, chỉ cần xóa nó khỏi danh sách hiện tại. Sau đó, cần thiết phải kiểm tra sự giao nhau của các hàng xóm trên và dưới trong danh sách.
- Không tồn tại các thay đổi khác trong chuỗi các đoạn thẳng trong danh sách, ngoại trừ những thay đổi được mô tả. Không cần kiểm tra giao nhau nào khác.
Để hiểu sự thật của các tuyên bố này, các nhận xét sau đây là đủ:
- Hai đoạn thẳng không giao nhau không bao giờ thay đổi thứ tự tương đối của chúng.
Thực tế, nếu một đoạn thẳng ban đầu cao hơn đoạn kia, và sau đó trở nên thấp hơn, thì giữa hai thời điểm này đã có sự giao nhau của hai đoạn thẳng này. - Hai đoạn thẳng không giao nhau cũng không thể có cùng tọa độ $y$.
- Từ điều này suy ra rằng tại thời điểm đoạn thẳng xuất hiện, chúng ta có thể tìm vị trí cho đoạn thẳng này trong hàng đợi, và chúng ta sẽ không phải sắp xếp lại đoạn thẳng này trong hàng đợi nữa: thứ tự của nó so với các đoạn thẳng khác trong hàng đợi sẽ không thay đổi.
- Hai đoạn thẳng giao nhau tại thời điểm điểm giao nhau của chúng sẽ là hàng xóm của nhau trong hàng đợi.
- Do đó, để tìm các cặp đoạn thẳng giao nhau là đủ để kiểm tra sự giao nhau của tất cả và chỉ những cặp đoạn thẳng mà đôi khi trong quá trình di chuyển của đường quét ít nhất một lần là hàng xóm của nhau.
Dễ nhận thấy rằng chỉ cần kiểm tra đoạn thẳng đã thêm với các hàng xóm trên và dưới của nó, cũng như khi xóa đoạn thẳng — các hàng xóm trên và dưới của nó (sau khi xóa sẽ trở thành hàng xóm của nhau). - Cần lưu ý rằng tại một vị trí cố định của đường quét, chúng ta phải thêm tất cả các đoạn thẳng trước bắt đầu tại tọa độ x này, và chỉ sau đó xóa tất cả các đoạn thẳng kết thúc tại đây.
Do đó, chúng ta không bỏ lỡ sự giao nhau của các đoạn thẳng trên đỉnh: tức là những trường hợp khi hai đoạn thẳng có chung một đỉnh. - Lưu ý rằng các đoạn thẳng đứng thực sự không ảnh hưởng đến tính đúng đắn của thuật toán.
Các đoạn thẳng này được phân biệt bởi thực tế là chúng xuất hiện và biến mất cùng một lúc. Tuy nhiên, do nhận xét trước đó, chúng ta biết rằng tất cả các đoạn thẳng sẽ được thêm vào hàng đợi trước, và chỉ sau đó chúng mới bị xóa. Do đó, nếu đoạn thẳng đứng cắt một đoạn thẳng nào đó khác đã mở tại thời điểm đó (bao gồm cả đoạn thẳng đứng), nó sẽ được phát hiện.
Đặt các đoạn thẳng đứng ở vị trí nào trong hàng đợi? Rốt cuộc, một đoạn thẳng đứng không có một tọa độ $y$ cụ thể, nó kéo dài cho cả một đoạn dọc theo tọa độ $y$. Tuy nhiên, dễ hiểu rằng bất kỳ tọa độ nào từ đoạn này đều có thể được lấy làm tọa độ $y$.
Do đó, toàn bộ thuật toán sẽ thực hiện không quá $2n$ bài kiểm tra về sự giao nhau của một cặp đoạn thẳng, và sẽ thực hiện $O(n)$ thao tác với một hàng đợi các đoạn thẳng ($O(1)$ thao tác tại thời điểm xuất hiện và biến mất của mỗi đoạn thẳng).
Hành vi tiệm cận của thuật toán (asymptotic behavior) cuối cùng do đó là $O(n \log n)$.
Cài đặt (Implementation)¶
Chúng tôi trình bày việc cài đặt đầy đủ của thuật toán được mô tả:
const double EPS = 1E-9;
struct pt {
double x, y;
};
struct seg {
pt p, q;
int id;
double get_y(double x) const {
if (abs(p.x - q.x) < EPS)
return p.y;
return p.y + (q.y - p.y) * (x - p.x) / (q.x - p.x);
}
};
bool intersect1d(double l1, double r1, double l2, double r2) {
if (l1 > r1)
swap(l1, r1);
if (l2 > r2)
swap(l2, r2);
return max(l1, l2) <= min(r1, r2) + EPS;
}
int vec(const pt& a, const pt& b, const pt& c) {
double s = (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
return abs(s) < EPS ? 0 : s > 0 ? +1 : -1;
}
bool intersect(const seg& a, const seg& b)
{
return intersect1d(a.p.x, a.q.x, b.p.x, b.q.x) &&
intersect1d(a.p.y, a.q.y, b.p.y, b.q.y) &&
vec(a.p, a.q, b.p) * vec(a.p, a.q, b.q) <= 0 &&
vec(b.p, b.q, a.p) * vec(b.p, b.q, a.q) <= 0;
}
bool operator<(const seg& a, const seg& b)
{
double x = max(min(a.p.x, a.q.x), min(b.p.x, b.q.x));
return a.get_y(x) < b.get_y(x) - EPS;
}
struct event {
double x;
int tp, id;
event() {}
event(double x, int tp, int id) : x(x), tp(tp), id(id) {}
bool operator<(const event& e) const {
if (abs(x - e.x) > EPS)
return x < e.x;
return tp > e.tp;
}
};
set<seg> s;
vector<set<seg>::iterator> where;
set<seg>::iterator prev(set<seg>::iterator it) {
return it == s.begin() ? s.end() : --it;
}
set<seg>::iterator next(set<seg>::iterator it) {
return ++it;
}
pair<int, int> solve(const vector<seg>& a) {
int n = (int)a.size();
vector<event> e;
for (int i = 0; i < n; ++i) {
e.push_back(event(min(a[i].p.x, a[i].q.x), +1, i));
e.push_back(event(max(a[i].p.x, a[i].q.x), -1, i));
}
sort(e.begin(), e.end());
s.clear();
where.resize(a.size());
for (size_t i = 0; i < e.size(); ++i) {
int id = e[i].id;
if (e[i].tp == +1) {
set<seg>::iterator nxt = s.lower_bound(a[id]), prv = prev(nxt);
if (nxt != s.end() && intersect(*nxt, a[id]))
return make_pair(nxt->id, id);
if (prv != s.end() && intersect(*prv, a[id]))
return make_pair(prv->id, id);
where[id] = s.insert(nxt, a[id]);
} else {
set<seg>::iterator nxt = next(where[id]), prv = prev(where[id]);
if (nxt != s.end() && prv != s.end() && intersect(*nxt, *prv))
return make_pair(prv->id, nxt->id);
s.erase(where[id]);
}
}
return make_pair(-1, -1);
}
Hàm chính ở đây là solve(), trả về các đoạn thẳng giao nhau nếu tồn tại, hoặc $(-1, -1)$, nếu không có giao điểm.
Kiểm tra giao điểm của hai đoạn thẳng được thực hiện bởi hàm intersect (), sử dụng thuật toán dựa trên diện tích có hướng của tam giác.
Hàng đợi các đoạn thẳng là biến toàn cục s, một set<event>. Các iterator chỉ định vị trí của mỗi đoạn thẳng trong hàng đợi (để thuận tiện cho việc xóa các đoạn thẳng khỏi hàng đợi) được lưu trữ trong mảng toàn cục where.
Hai hàm phụ trợ prev() và next() cũng được giới thiệu, trả về các iterator đến các phần tử trước đó và tiếp theo (hoặc end(), nếu không tồn tại).
Hằng số EPS biểu thị sai số của việc so sánh hai số thực (nó chủ yếu được sử dụng khi kiểm tra hai đoạn thẳng giao nhau).