Tìm các mặt của đồ thị phẳng (Finding faces of a planar graph)¶
Xem xét một đồ thị $G$ với $n$ đỉnh và $m$ cạnh, có thể được vẽ trên một mặt phẳng theo cách mà hai cạnh chỉ cắt nhau tại một đỉnh chung (nếu nó tồn tại). Các đồ thị như vậy được gọi là đồ thị phẳng (planar). Bây giờ giả sử rằng chúng ta được cho một đồ thị phẳng cùng với phép nhúng đường thẳng (straight-line embedding) của nó, có nghĩa là đối với mỗi đỉnh $v$ chúng ta có một điểm tương ứng $(x, y)$ và tất cả các cạnh được vẽ dưới dạng các đoạn thẳng giữa các điểm này mà không cắt nhau (phép nhúng như vậy luôn tồn tại). Các đoạn thẳng này chia mặt phẳng thành một số vùng, được gọi là các mặt (faces). Chính xác một trong các mặt là không bị giới hạn. Mặt này được gọi là mặt ngoài (outer), trong khi các mặt khác được gọi là mặt trong (inner).
Trong bài viết này, chúng ta sẽ giải quyết việc tìm cả mặt trong và mặt ngoài của một đồ thị phẳng. Chúng ta sẽ giả sử rằng đồ thị là liên thông.
Một số sự thật về đồ thị phẳng (Some facts about planar graphs)¶
Trong phần này, chúng tôi trình bày một số sự thật về đồ thị phẳng mà không cần chứng minh. Độc giả quan tâm đến các chứng minh nên tham khảo Lý thuyết đồ thị của R. Diestel (xem thêm video bài giảng về tính phẳng dựa trên cuốn sách này) hoặc một số cuốn sách khác.
Định lý Euler (Euler's theorem)¶
Định lý Euler phát biểu rằng bất kỳ phép nhúng chính xác nào của một đồ thị phẳng liên thông với $n$ đỉnh, $m$ cạnh và $f$ mặt đều thỏa mãn:
Và tổng quát hơn, mọi đồ thị phẳng với $k$ thành phần liên thông thỏa mãn:
Số lượng cạnh của đồ thị phẳng (Number of edges of a planar graph)¶
Nếu $n \ge 3$ thì số lượng cạnh tối đa của một đồ thị phẳng với $n$ đỉnh là $3n - 6$. Số lượng này đạt được bởi bất kỳ đồ thị phẳng liên thông nào trong đó mỗi mặt được giới hạn bởi một tam giác. Về mặt độ phức tạp, thực tế này có nghĩa là $m = O(n)$ cho bất kỳ đồ thị phẳng nào.
Số lượng mặt của đồ thị phẳng (Number of faces of a planar graph)¶
Như một hệ quả trực tiếp của thực tế trên, nếu $n \ge 3$ thì số lượng mặt tối đa của một đồ thị phẳng với $n$ đỉnh là $2n - 4$.
Bậc đỉnh tối thiểu trong đồ thị phẳng (Minimum vertex degree in a planar graph)¶
Mọi đồ thị phẳng đều có một đỉnh bậc 5 trở xuống.
Thuật toán (The algorithm)¶
Trước tiên, hãy sắp xếp các cạnh kề cho mỗi đỉnh theo góc cực. Bây giờ hãy duyệt đồ thị theo cách sau. Giả sử rằng chúng ta đã vào đỉnh $u$ thông qua cạnh $(v, u)$ và $(u, w)$ là cạnh tiếp theo sau $(v, u)$ trong danh sách kề đã được sắp xếp của $u$. Khi đó đỉnh tiếp theo sẽ là $w$. Hóa ra nếu chúng ta bắt đầu quá trình duyệt này tại một cạnh $(v, u)$ nào đó, chúng ta sẽ duyệt chính xác một trong các mặt kề với $(v, u)$, mặt chính xác phụ thuộc vào việc bước đầu tiên của chúng ta là từ $u$ đến $v$ hay từ $v$ đến $u$.
Bây giờ thuật toán khá rõ ràng. Chúng ta phải lặp qua tất cả các cạnh của đồ thị và bắt đầu duyệt cho mỗi cạnh chưa được thăm bởi một trong những lần duyệt trước đó. Bằng cách này, chúng ta sẽ tìm thấy mỗi mặt chính xác một lần, và mỗi cạnh sẽ được duyệt hai lần (một lần theo mỗi hướng).
Tìm cạnh tiếp theo (Finding the next edge)¶
Trong quá trình duyệt, chúng ta phải tìm cạnh tiếp theo theo thứ tự ngược chiều kim đồng hồ. Cách rõ ràng nhất để tìm cạnh tiếp theo là tìm kiếm nhị phân theo góc. Tuy nhiên, với thứ tự ngược chiều kim đồng hồ của các cạnh kề cho mỗi đỉnh, chúng ta có thể tính toán trước các cạnh tiếp theo và lưu trữ chúng trong bảng băm. Nếu các cạnh đã được sắp xếp theo góc, độ phức tạp của việc tìm tất cả các mặt trong trường hợp này trở thành tuyến tính.
Tìm mặt ngoài (Finding the outer face)¶
Không khó để thấy rằng thuật toán duyệt từng mặt trong theo thứ tự cùng chiều kim đồng hồ và mặt ngoài theo thứ tự ngược chiều kim đồng hồ, vì vậy mặt ngoài có thể được tìm thấy bằng cách kiểm tra thứ tự của từng mặt.
Độ phức tạp (Complexity)¶
Khá rõ ràng rằng độ phức tạp của thuật toán là $O(m \log m)$ do việc sắp xếp, và vì $m = O(n)$, nó thực sự là $O(n \log n)$. Như đã đề cập trước đó, nếu không cần sắp xếp thì độ phức tạp trở thành $O(n)$.
Điều gì xảy ra nếu đồ thị không liên thông? (What if the graph isn't connected?)¶
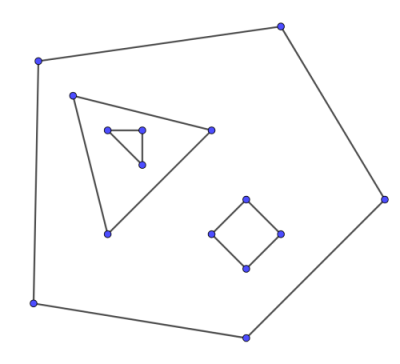
Thoạt nhìn, có vẻ như việc tìm các mặt của đồ thị không liên thông không khó hơn nhiều vì chúng ta có thể chạy cùng một thuật toán cho từng thành phần liên thông. Tuy nhiên, các thành phần có thể được vẽ theo kiểu lồng nhau, tạo thành các lỗ (holes) (xem hình ảnh bên dưới). Trong trường hợp này, mặt trong của một số thành phần trở thành mặt ngoài của một số thành phần khác và có biên giới không liên thông phức tạp. Việc giải quyết các trường hợp như vậy khá khó khăn, một cách tiếp cận khả thi là xác định các thành phần lồng nhau bằng các thuật toán định vị điểm.
Cài đặt (Implementation)¶
Việc cài đặt sau đây trả về một vector các đỉnh cho mỗi mặt, mặt ngoài đi trước. Các mặt trong được trả về theo thứ tự ngược chiều kim đồng hồ và mặt ngoài được trả về theo thứ tự cùng chiều kim đồng hồ.
Để đơn giản, chúng ta tìm cạnh tiếp theo bằng cách thực hiện tìm kiếm nhị phân theo góc.
struct Point {
int64_t x, y;
Point(int64_t x_, int64_t y_): x(x_), y(y_) {}
Point operator - (const Point & p) const {
return Point(x - p.x, y - p.y);
}
int64_t cross (const Point & p) const {
return x * p.y - y * p.x;
}
int64_t cross (const Point & p, const Point & q) const {
return (p - *this).cross(q - *this);
}
int half () const {
return int(y < 0 || (y == 0 && x < 0));
}
};
std::vector<std::vector<size_t>> find_faces(std::vector<Point> vertices, std::vector<std::vector<size_t>> adj) {
size_t n = vertices.size();
std::vector<std::vector<char>> used(n);
for (size_t i = 0; i < n; i++) {
used[i].resize(adj[i].size());
used[i].assign(adj[i].size(), 0);
auto compare = [&](size_t l, size_t r) {
Point pl = vertices[l] - vertices[i];
Point pr = vertices[r] - vertices[i];
if (pl.half() != pr.half())
return pl.half() < pr.half();
return pl.cross(pr) > 0;
};
std::sort(adj[i].begin(), adj[i].end(), compare);
}
std::vector<std::vector<size_t>> faces;
for (size_t i = 0; i < n; i++) {
for (size_t edge_id = 0; edge_id < adj[i].size(); edge_id++) {
if (used[i][edge_id]) {
continue;
}
std::vector<size_t> face;
size_t v = i;
size_t e = edge_id;
while (!used[v][e]) {
used[v][e] = true;
face.push_back(v);
size_t u = adj[v][e];
size_t e1 = std::lower_bound(adj[u].begin(), adj[u].end(), v, [&](size_t l, size_t r) {
Point pl = vertices[l] - vertices[u];
Point pr = vertices[r] - vertices[u];
if (pl.half() != pr.half())
return pl.half() < pr.half();
return pl.cross(pr) > 0;
}) - adj[u].begin() + 1;
if (e1 == adj[u].size()) {
e1 = 0;
}
v = u;
e = e1;
}
std::reverse(face.begin(), face.end());
Point p1 = vertices[face[0]];
__int128 sum = 0;
for (int j = 0; j < face.size(); ++j) {
Point p2 = vertices[face[j]];
Point p3 = vertices[face[(j + 1) % face.size()]];
sum += (p2 - p1).cross(p3 - p2);
}
if (sum <= 0) {
faces.insert(faces.begin(), face);
} else {
faces.emplace_back(face);
}
}
}
return faces;
}
Xây dựng đồ thị phẳng từ các đoạn thẳng (Building planar graph from line segments)¶
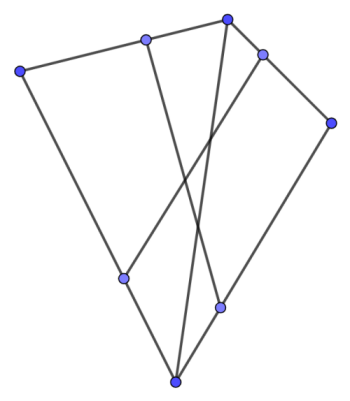
Đôi khi bạn không được cung cấp một đồ thị một cách rõ ràng, mà thay vào đó là một tập hợp các đoạn thẳng trên một mặt phẳng, và đồ thị thực tế được hình thành bằng cách cắt các đoạn thẳng đó, như trong hình bên dưới. Trong trường hợp này, bạn phải xây dựng đồ thị thủ công. Cách dễ nhất để làm điều đó là như sau. Cố định một đoạn thẳng và cắt nó với tất cả các đoạn thẳng khác. Sau đó sắp xếp tất cả các điểm giao nhau cùng với hai đầu mút của đoạn thẳng theo thứ tự từ điển và thêm chúng vào đồ thị dưới dạng các đỉnh. Cũng liên kết mỗi hai đỉnh liền kề theo thứ tự từ điển bằng một cạnh. Sau khi thực hiện quy trình này cho tất cả các cạnh, chúng ta sẽ thu được đồ thị. Tất nhiên, chúng ta nên đảm bảo rằng hai điểm giao nhau bằng nhau sẽ luôn tương ứng với cùng một đỉnh. Cách dễ nhất để làm điều này là lưu trữ các điểm trong một map theo tọa độ của chúng, coi các điểm có tọa độ khác nhau một số nhỏ (giả sử, nhỏ hơn $10^{-9}$) là bằng nhau. Thuật toán này hoạt động trong $O(n^2 \log n)$.
Cài đặt (Implementation)¶
using dbl = long double;
const dbl eps = 1e-9;
struct Point {
dbl x, y;
Point(){}
Point(dbl x_, dbl y_): x(x_), y(y_) {}
Point operator * (dbl d) const {
return Point(x * d, y * d);
}
Point operator + (const Point & p) const {
return Point(x + p.x, y + p.y);
}
Point operator - (const Point & p) const {
return Point(x - p.x, y - p.y);
}
dbl cross (const Point & p) const {
return x * p.y - y * p.x;
}
dbl cross (const Point & p, const Point & q) const {
return (p - *this).cross(q - *this);
}
dbl dot (const Point & p) const {
return x * p.x + y * p.y;
}
dbl dot (const Point & p, const Point & q) const {
return (p - *this).dot(q - *this);
}
bool operator < (const Point & p) const {
if (fabs(x - p.x) < eps) {
if (fabs(y - p.y) < eps) {
return false;
} else {
return y < p.y;
}
} else {
return x < p.x;
}
}
bool operator == (const Point & p) const {
return fabs(x - p.x) < eps && fabs(y - p.y) < eps;
}
bool operator >= (const Point & p) const {
return !(*this < p);
}
};
struct Line{
Point p[2];
Line(Point l, Point r){p[0] = l; p[1] = r;}
Point& operator [](const int & i){return p[i];}
const Point& operator[](const int & i)const{return p[i];}
Line(const Line & l){
p[0] = l.p[0]; p[1] = l.p[1];
}
Point getOrth()const{
return Point(p[1].y - p[0].y, p[0].x - p[1].x);
}
bool hasPointLine(const Point & t)const{
return std::fabs(p[0].cross(p[1], t)) < eps;
}
bool hasPointSeg(const Point & t)const{
return hasPointLine(t) && t.dot(p[0], p[1]) < eps;
}
};
std::vector<Point> interLineLine(Line l1, Line l2){
if(std::fabs(l1.getOrth().cross(l2.getOrth())) < eps){
if(l1.hasPointLine(l2[0]))return {l1[0], l1[1]};
else return {};
}
Point u = l2[1] - l2[0];
Point v = l1[1] - l1[0];
dbl s = u.cross(l2[0] - l1[0])/u.cross(v);
return {Point(l1[0] + v * s)};
}
std::vector<Point> interSegSeg(Line l1, Line l2){
if (l1[0] == l1[1]) {
if (l2[0] == l2[1]) {
if (l1[0] == l2[0])
return {l1[0]};
else
return {};
} else {
if (l2.hasPointSeg(l1[0]))
return {l1[0]};
else
return {};
}
}
if (l2[0] == l2[1]) {
if (l1.hasPointSeg(l2[0]))
return {l2[0]};
else
return {};
}
auto li = interLineLine(l1, l2);
if (li.empty())
return li;
if (li.size() == 2) {
if (l1[0] >= l1[1])
std::swap(l1[0], l1[1]);
if (l2[0] >= l2[1])
std::swap(l2[0], l2[1]);
std::vector<Point> res(2);
if (l1[0] < l2[0])
res[0] = l2[0];
else
res[0] = l1[0];
if (l1[1] < l2[1])
res[1] = l1[1];
else
res[1] = l2[1];
if (res[0] == res[1])
res.pop_back();
if (res.size() == 2u && res[1] < res[0])
return {};
else
return res;
}
Point cand = li[0];
if (l1.hasPointSeg(cand) && l2.hasPointSeg(cand))
return {cand};
else
return {};
}
std::pair<std::vector<Point>, std::vector<std::vector<size_t>>> build_graph(std::vector<Line> segments) {
std::vector<Point> p;
std::vector<std::vector<size_t>> adj;
std::map<std::pair<int64_t, int64_t>, size_t> point_id;
auto get_point_id = [&](Point pt) {
auto repr = std::make_pair(
int64_t(std::round(pt.x * 1000000000) + 1e-6),
int64_t(std::round(pt.y * 1000000000) + 1e-6)
);
if (!point_id.count(repr)) {
adj.emplace_back();
size_t id = point_id.size();
point_id[repr] = id;
p.push_back(pt);
return id;
} else {
return point_id[repr];
}
};
for (size_t i = 0; i < segments.size(); i++) {
std::vector<size_t> curr = {
get_point_id(segments[i][0]),
get_point_id(segments[i][1])
};
for (size_t j = 0; j < segments.size(); j++) {
if (i == j)
continue;
auto inter = interSegSeg(segments[i], segments[j]);
for (auto pt: inter) {
curr.push_back(get_point_id(pt));
}
}
std::sort(curr.begin(), curr.end(), [&](size_t l, size_t r) { return p[l] < p[r]; });
curr.erase(std::unique(curr.begin(), curr.end()), curr.end());
for (size_t j = 0; j + 1 < curr.size(); j++) {
adj[curr[j]].push_back(curr[j + 1]);
adj[curr[j + 1]].push_back(curr[j]);
}
}
for (size_t i = 0; i < adj.size(); i++) {
std::sort(adj[i].begin(), adj[i].end());
// removing edges that were added multiple times
adj[i].erase(std::unique(adj[i].begin(), adj[i].end()), adj[i].end());
}
return {p, adj};
}