Phương pháp Newton để tìm nghiệm (Newton's method for finding roots)¶
Đây là một phương pháp lặp được Isaac Newton phát minh vào khoảng năm 1664. Tuy nhiên, phương pháp này đôi khi còn được gọi là phương pháp Raphson, vì Raphson đã phát minh ra cùng một thuật toán một vài năm sau Newton, nhưng bài báo của ông đã được xuất bản sớm hơn nhiều.
Nhiệm vụ như sau. Cho phương trình sau:
Chúng tôi muốn giải phương trình. Chính xác hơn, chúng tôi muốn tìm một trong những nghiệm của nó (giả sử rằng nghiệm tồn tại). Giả sử rằng $f(x)$ liên tục và có thể vi phân trên một khoảng $[a, b]$.
Thuật toán (Algorithm)¶
Các tham số đầu vào của thuật toán không chỉ bao gồm hàm $f(x)$ mà còn cả xấp xỉ ban đầu - một số $x_0$, mà thuật toán bắt đầu với nó.
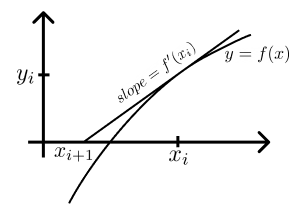
Giả sử chúng ta đã tính toán $x_i$, hãy tính $x_{i+1}$ như sau. Vẽ tiếp tuyến với đồ thị của hàm $f(x)$ tại điểm $x = x_i$, và tìm điểm giao nhau của tiếp tuyến này với trục $x$. $x_{i+1}$ được đặt bằng toạ độ $x$ của điểm tìm được, và chúng ta lặp lại toàn bộ quá trình từ đầu.
Không khó để có được công thức sau,
Đầu tiên, chúng ta tính độ dốc $f'(x)$, đạo hàm của $f(x)$, và sau đó xác định phương trình của tiếp tuyến là,
Tiếp tuyến giao với trục x tại tọa độ, $y = 0$ và $x = x_{i+1}$,
Bây giờ, giải phương trình ta được giá trị của $x_{i+1}$.
Về mặt trực quan, rõ ràng là nếu hàm $f(x)$ là "tốt" (trơn), và $x_i$ đủ gần với nghiệm, thì $x_{i+1}$ thậm chí sẽ gần hơn với nghiệm mong muốn.
Tốc độ hội tụ là bậc hai, nói một cách có điều kiện, có nghĩa là số lượng chữ số chính xác trong giá trị gần đúng $x_i$ tăng gấp đôi sau mỗi lần lặp.
Ứng dụng để tính căn bậc hai (Application for calculating the square root)¶
Hãy sử dụng phép tính căn bậc hai làm ví dụ về phương pháp Newton.
Nếu chúng ta thay thế $f(x) = x^2 - n$, thì sau khi đơn giản hóa biểu thức, chúng ta nhận được:
Biến thể điển hình đầu tiên của bài toán là khi một số hữu tỉ $n$ được đưa ra, và căn bậc của nó phải được tính toán với độ chính xác nào đó eps:
double sqrt_newton(double n) {
const double eps = 1E-15;
double x = 1;
for (;;) {
double nx = (x + n / x) / 2;
if (abs(x - nx) < eps)
break;
x = nx;
}
return x;
}
Một biến thể phổ biến khác của bài toán là khi chúng ta cần tính căn bậc hai nguyên (đối với $n$ đã cho tìm $x$ lớn nhất sao cho $x^2 \le n$). Ở đây cần thay đổi một chút điều kiện chấm dứt của thuật toán, vì có thể xảy ra trường hợp $x$ sẽ bắt đầu "nhảy" gần câu trả lời. Do đó, chúng tôi thêm một điều kiện rằng nếu giá trị $x$ đã giảm trong bước trước đó, và nó cố gắng tăng ở bước hiện tại, thì thuật toán phải dừng lại.
int isqrt_newton(int n) {
int x = 1;
bool decreased = false;
for (;;) {
int nx = (x + n / x) >> 1;
if (x == nx || nx > x && decreased)
break;
decreased = nx < x;
x = nx;
}
return x;
}
Cuối cùng, chúng ta được đưa ra biến thể thứ ba - cho trường hợp số học số lớn (bignum arithmetic). Vì số $n$ có thể đủ lớn, nên chú ý đến xấp xỉ ban đầu. Rõ ràng, càng gần nghiệm, kết quả sẽ càng nhanh đạt được. Đủ đơn giản và hiệu quả để lấy xấp xỉ ban đầu là số $2^{\textrm{bits}/2}$, trong đó $\textrm{bits}$ là số bit trong số $n$. Đây là mã Java thể hiện biến thể này:
public static BigInteger isqrtNewton(BigInteger n) {
BigInteger a = BigInteger.ONE.shiftLeft(n.bitLength() / 2);
boolean p_dec = false;
for (;;) {
BigInteger b = n.divide(a).add(a).shiftRight(1);
if (a.compareTo(b) == 0 || a.compareTo(b) < 0 && p_dec)
break;
p_dec = a.compareTo(b) > 0;
a = b;
}
return a;
}
Ví dụ, mã này được thực thi trong $60$ mili giây cho $n = 10^{1000}$, và nếu chúng ta loại bỏ lựa chọn cải tiến của xấp xỉ ban đầu (chỉ bắt đầu bằng $1$), thì nó sẽ được thực thi trong khoảng $120$ mili giây.