Điểm nguyên bên trong đa giác không nguyên (Lattice points inside non-lattice polygon)¶
Đối với các đa giác nguyên (đa giác có các đỉnh là điểm nguyên), đã có công thức Pick để liệt kê các điểm nguyên bên trong đa giác. Còn đối với các đa giác có các đỉnh tùy ý thì sao?
Hãy xử lý từng cạnh của đa giác một cách riêng lẻ, và sau đó chúng ta có thể cộng tổng số lượng các điểm nguyên bên dưới mỗi cạnh, xem xét hướng của nó để chọn dấu (giống như trong việc tính diện tích của một đa giác bằng cách sử dụng các hình thang).
Trước hết, chúng ta nên lưu ý rằng nếu cạnh hiện tại có các điểm đầu mút tại $A=(x_1;y_1)$ và $B=(x_2;y_2)$ thì nó có thể được biểu diễn dưới dạng một hàm tuyến tính:
Bây giờ chúng ta sẽ thực hiện một phép thay thế $x=x'+\lceil x_1 \rceil$ để $b' = b + k \cdot \lceil x_1 \rceil$. Điều này cho phép chúng ta làm việc với $x_1'=0$ và $x_2'=x_2 - \lceil x_1 \rceil$. Hãy ký hiệu $n = \lfloor x_2' \rfloor$.
Chúng ta sẽ không cộng tổng các điểm tại $x = n$ và trên $y = 0$ cho tính toàn vẹn của thuật toán. Chúng có thể được thêm vào thủ công sau đó. Do đó chúng ta phải tính tổng $\sum\limits_{x'=0}^{n - 1} \lfloor k' \cdot x' + b'\rfloor$. Chúng ta cũng giả sử rằng $k' \geq 0$ và $b'\geq 0$. Nếu không, người ta nên thay thế $x'=-t$ và thêm $\lceil|b'|\rceil$ vào $b'$.
Hãy thảo luận về cách chúng ta có thể đánh giá tổng $\sum\limits_{x=0}^{n - 1} \lfloor k \cdot x + b\rfloor$. Chúng ta có hai trường hợp:
-
$k \geq 1$ hoặc $b \geq 1$.
Khi đó chúng ta nên bắt đầu bằng cách cộng tổng các điểm bên dưới $y=\lfloor k \rfloor \cdot x + \lfloor b \rfloor$. Số lượng của chúng bằng
$$ \sum\limits_{x=0}^{n - 1} \lfloor k \rfloor \cdot x + \lfloor b \rfloor=\dfrac{(\lfloor k \rfloor(n-1)+2\lfloor b \rfloor) n}{2}. $$Bây giờ chúng ta chỉ quan tâm đến các điểm $(x;y)$ sao cho $\lfloor k \rfloor \cdot x + \lfloor b \rfloor < y \leq k\cdot x + b$. Số lượng này cũng giống như số lượng các điểm sao cho $0 < y \leq (k - \lfloor k \rfloor) \cdot x + (b - \lfloor b \rfloor)$. Vì vậy, chúng ta đã giảm bài toán của mình thành $k'= k - \lfloor k \rfloor$, $b' = b - \lfloor b \rfloor$ và cả $k'$ và $b'$ hiện đều nhỏ hơn $1$. Dưới đây là một hình ảnh, chúng ta chỉ cần cộng tổng các điểm màu xanh lam và trừ đi hàm tuyến tính màu xanh lam khỏi hàm màu đen để giảm bài toán xuống các giá trị nhỏ hơn cho $k$ và $b$:
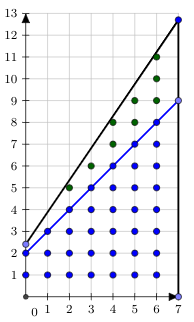
-
$k < 1$ và $b < 1$.
Nếu $\lfloor k \cdot n + b\rfloor$ bằng $0$, chúng ta có thể trả về $0$ một cách an toàn. Nếu không phải trường hợp này, chúng ta có thể nói rằng không có điểm nguyên nào sao cho $x < 0$ và $0 < y \leq k \cdot x + b$. Điều đó có nghĩa là chúng ta sẽ có cùng một câu trả lời nếu chúng ta xem xét hệ quy chiếu mới trong đó $O'=(n;\lfloor k\cdot n + b\rfloor)$, trục $x'$ hướng xuống dưới và trục $y'$ hướng sang trái. Đối với hệ quy chiếu này, chúng ta quan tâm đến các điểm nguyên trên tập hợp
$$ \left\{(x;y)~\bigg|~0 \leq x < \lfloor k \cdot n + b\rfloor,~ 0 < y \leq \dfrac{x+(k\cdot n+b)-\lfloor k\cdot n + b \rfloor}{k}\right\} $$trả lại chúng ta về trường hợp $k>1$. Bạn có thể thấy điểm tham chiếu mới $O'$ và các trục $X'$ và $Y'$ trong hình dưới đây:
Như bạn thấy, trong hệ quy chiếu mới, hàm tuyến tính sẽ có hệ số $\tfrac 1 k$ và điểm không của nó sẽ ở điểm $\lfloor k\cdot n + b \rfloor-(k\cdot n+b)$ làm cho công thức trên đúng.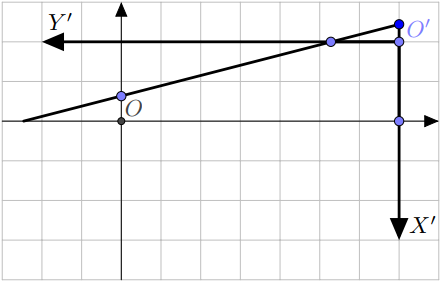
Phân tích độ phức tạp (Complexity analysis)¶
Chúng ta phải đếm tối đa $\dfrac{(k(n-1)+2b)n}{2}$ điểm. Trong số đó, chúng ta sẽ đếm $\dfrac{\lfloor k \rfloor (n-1)+2\lfloor b \rfloor}{2}$ ở ngay bước đầu tiên. Chúng ta có thể coi $b$ là nhỏ không đáng kể vì chúng ta có thể bắt đầu bằng cách làm cho nó nhỏ hơn $1$. Trong trường hợp đó, chúng ta có thể nói rằng chúng ta đếm khoảng $\dfrac{\lfloor k \rfloor}{k} \geq \dfrac 1 2$ tất cả các điểm. Do đó, chúng ta sẽ kết thúc trong $O(\log n)$ bước.
Cài đặt (Implementation)¶
Dưới đây là hàm đơn giản tính toán số lượng điểm nguyên $(x;y)$ sao cho với $0 \leq x < n$ và $0 < y \leq \lfloor k x+b\rfloor$:
int count_lattices(Fraction k, Fraction b, long long n) {
auto fk = k.floor();
auto fb = b.floor();
auto cnt = 0LL;
if (k >= 1 || b >= 1) {
cnt += (fk * (n - 1) + 2 * fb) * n / 2;
k -= fk;
b -= fb;
}
auto t = k * n + b;
auto ft = t.floor();
if (ft >= 1) {
cnt += count_lattices(1 / k, (t - t.floor()) / k, t.floor());
}
return cnt;
}
Ở đây Fraction là một lớp xử lý số hữu tỉ.
Trên thực tế, có vẻ như nếu tất cả các mẫu số và tử số đều tối đa là $C$ theo giá trị tuyệt đối thì trong các lệnh gọi đệ quy, chúng sẽ tối đa là $C^2$ nếu bạn liên tục chia cả tử số và mẫu số cho ước chung lớn nhất của chúng.
Với giả định này, chúng ta có thể nói rằng người ta có thể sử dụng kiểu double và yêu cầu độ chính xác là $\varepsilon^2$ trong đó $\varepsilon$ là độ chính xác mà $k$ và $b$ được đưa ra.
Điều đó có nghĩa là trong hàm floor người ta nên coi các số là số nguyên nếu chúng khác số nguyên tối đa một lượng $\varepsilon^2$.